中考第一次模拟考试数学试题-初中三年级数学试题练习、期中期末试卷、测验题、复习资料-初中数学试卷-试卷下载

中考第一次模拟考试数学试题

注意事项：

1、答题前务必将姓名、准考证号、科目用铅笔涂写在答题卡上。

2、选出答案后，用铅笔将对应题目的答案标号涂黑，答在试卷上无效。

3、考试结束后，将答题卡和试卷一并交回。

一、选择题（本大题有10小题，每小题3分，共30分）

1．下列计算结果是－2的是(　 )

A．2^-1　　　　B．（－2）⁰　　　　C．－（－2）　　　　 D．－

2．下列各式中，相等关系一定成立的是(　 )

A．　　　　　 B．

C．　　　　　D．

3．下列命题中的假命题是 (　 )

A．和是同类二次根式　B．相切两圆的圆心和切点一定在同一直线上

C．抛物线的顶点坐标是(2,－1)　　D．当x＝－1时,分式的值为0

4．如果实数a、b使成立，那么点（a，b）在(　 )

A．第二象限　　B．第三象限　　　C．第二象限或坐标轴上　D．第四象限或坐标轴上

5．小明在镜子中发现自己运动衣上的号码如图所示.你能知道小明运动衣上的号码是（　　）

A．8002　　　　B．8005　　　　 C．5008 　　 D．2008

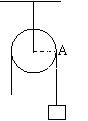6．一个定滑轮装置如图，滑轮的半径是10cm，当重物上升10cm时滑轮的一条半径OA绕轴心O按逆时针方向旋转的角度约为（假设绳索与滑轮之间没有滑动，结果精确到1°）（　　）

A．115°　　 B．60°　　　　 C．57°　　 D．以上都不对

7．用换元法解分式方程时，若设则原方程可化为关于y的整式方程是(　 )

A．　B．　 C．　　D．

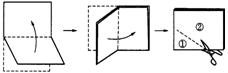8．将一张矩形纸对折再对折（如图），然后沿着图中的虚线剪下，得到①、②两部分，将①展开后得到的平面图形是（　　）

A．矩形　 B．三角形　C．梯形　 D．菱形

9．如图，正方形硬纸片ABCD的边长是4，点E、F分别是AB、BC的中点，若沿左图中的虚线剪开，拼成如下右图的一座“小别墅”，则图中阴影部分的面积是

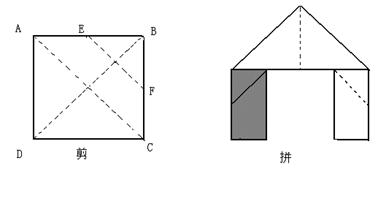A．2　　　　 B．4　　　　 C．8　　　　D．10

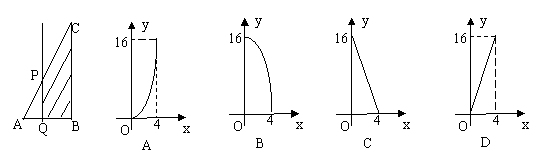10．如图RT△ABC中，∠C=90°，AC=4，BC=8，P是AB上一动点，直线PQ⊥AC与点Q，设AQ=x,则图中阴影部分的面积y与x之间的函数关系的图象是（　　）

二、填空题（本大题有8小题，每小题3分，共24分）

11．根据国家统计局公布,2005年我国全年国内生产总值为182521亿元,用科学记数法表示为_________________亿元(结果保留3个有效数字).

12．函数中自变量x的取值范围是______.

13．如图AB、AC与⊙O相切于B、C，∠A=50°，点P

是圆上异于B、C的一动点，则∠BPC的度数是______.

14．已知线段AB＝4，BC＝3，那么线段AC的长度的取值范围是　　　　　 .

15．在△ABC中，∠C=90°，AC=6，BC=8，现以AC所在直线为轴，旋转一周得到一个圆锥。则该圆锥的表面积为_______________.

16．已知实数x满足,那么的值为__________.

17．关于x的一元二次方程有两个不相等的正根．则a可取的值为　　　　 .（注：只要填写一个可能的数值即可．）

18．小王利用计算机设计了一个计算程序，输入和输出的数据如下表：

输入	…	1	2	3	4	5	…
输出	…						…

那么，当输入数据是8时，根据上表中的规律,输出的数据是______________.

三、解答题（本大题共12小题，计96分）

19．（5分）计算：

20．（5分）已知，求的值．

21.（6分）如图,E、F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE ,DF∥BE. 试问四边形ABCD是平行四边形吗,为什么?

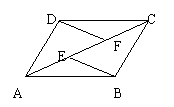22. (8分)已知:、是一元二次方程的两个实数根.

⑴ 求实数的取值范围;

⑵ 如果、满足不等式,且为整数,求的值.

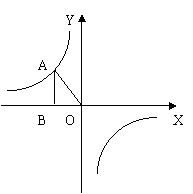
23．（8分）已知：如图,反比例函数的图象经过点A(),过A作AB⊥x轴于点B,△AOB的面积为.⑴ 求k和m的值；⑵若过A点直线与x轴正半轴交于点C,且∠ACO=30°,　求此直线的解析式.

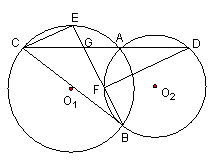
24．（8分）如图，⊙O₁与⊙O₂相交于点A、B，过点A的直线分别交⊙O₁、⊙O₂于点C、D，E为上一点，直线BE交⊙O₂于点F，交AC于点G.

⑴ 求证：CE∥FD.

⑵ 若E为的中点，求证：△ECG～△EBC.

⑶ 在⑵的条件下，当等于多少时，有？请说明理由.

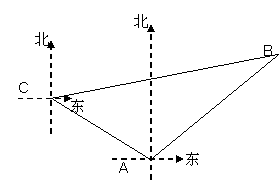
25．（8分）如图，甲、乙两只捕捞船同时从A港出海捕鱼.甲船以每小时千米的速度沿西偏北30°方向前进，乙船以每小时15千米的速度沿东北方向前进.甲船航行2小时到达C处，此时甲船发现渔具丢在乙船上，于是甲船快速(匀速)沿北偏东75°的方向追赶，结果两船在B处相遇.

⑴ 甲船从C处追赶上乙船用了多少时间？

⑵ 甲船追赶乙船的速度是每小时多少千米？(结果保留根式)

26．(8分)某中学为了解初三男生的身高情况，抽测了50名男生的身高，数据如下：（单

位：米）

身高	1.57	1.60	1.62	1.64	1.65	1.66	1.67	1.68	1.69
人数	1	1	1	3	3	3	2	4	6
身高	1.70	1.71	1.72	1.73	1.74	1.75	1.76	1.78	1.80
人数	7	7	2	3	2	1	2	1	1

⑴ 若将数据分成6组，取组距为0.04米，试完成相应的频率分布表：

分组

1.565

～1.605

1.605

～1.645

1.645

～1.685

1.685

～1.725

1.725

～1.765

1.765

～1.805

合计

频数

频率

0.04

0.08

0.44

0.16

0.04

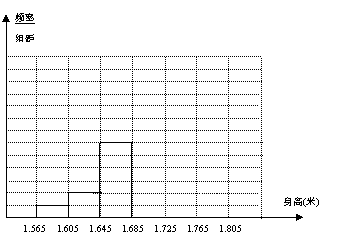⑵ 补全频率分布直方图：

⑶ 根据样本数据，求该校初三男生身高的中位数为　　　　　米；身高在1.695～1.755米之间的男生所占的百分比为　　　　　，如果该校初三共有450名男生，那么在

1.695～1.755米之间的人数约为

____ 人.

27．(8分)将正方形ABCD折叠，使顶点A与CD边上的点M重合，折痕交AD于E，交BC于F，边AB折叠后与BC边交于点G（如图）.

⑴如果M为CD边的中点，求证：DE∶DM∶EM=3∶4∶5；

⑵如果M为CD边上的任意一点，设AB=2a，问△CMG的周长是否与点M的位置有关？若有关，请把△CMG的周长用含DM的长x的代数式表示；若无关，请说明理由.

28．(8分)亭湖区张庄葡萄色润味美，畅销大江南北.它从树上摘下后不保鲜最多只能存放一周，如果放在冷藏室，可以延长保鲜时间，但每天仍有一定数量的葡萄变质，假设保鲜期内的个体质量基本保持不变，王老板某日批发200kg的这种葡萄放在冷藏室内，此时市场价为2元／千克，据测算，此后的每千克葡萄每天可上涨0.2元，但是，存放一天需各种费用为20元，且平均每天还有1千克的葡萄变质丢弃 .

⑴设x天后的这种葡萄市场价为p元／千克，写出p与x的函数关系式；

⑵若存放x天后将葡萄一次性出售，设葡萄的销售总金额为y元，写出y关于x的函数关系式；

⑶该个体户将这批葡萄存放多少天后出售，可获得最大利润Q？最大利润Q是多少？（本题不要求写出自变量x 的取值范围）

29．(12分)操作：将一把三角尺放在边长为1的正方形ABCD上，并使它的直角顶点P在对角线AC上滑动，直角的一边始终经过点B，另一边与射线DC相交于点Q。

探究：设A、P两点间的距离为x。

⑴当点Q在边CD上时，线段PQ于线段PB之间又怎样的大小关系？请证明你观察得到的结论.

⑵当点Q在边CD上时，设四边形PBCQ的面积为y，求y于x之间的函数关系式，并写出自变量的取值范围.

⑶当点P在线段AC上滑动时，△PCQ是否可能成为等腰三角形？如果可能，指出所有能使△PCQ成为等腰三角形的点Q的位置，并求出相应的x的值；如果不可能，试说明理由.

　（图1、图2、图3的形状大小相同，图一供操作、试验用，图2和图3备用）

　A　　　　　　 D　　　　　　 A　　　　　　 D　　　　　 A　　　　　　D

　　　 B　　　　　　 C　　　　　　 B　　　　　 C 　　　　　 B　　　　　 C

　　　　图1　　　　　　　　　　　图2　　　　　　　　　　　图3

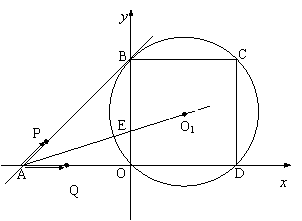
30．(12分)已知一次函数的图像分别交轴、轴于A、B两点，⊙O₁过以OB为边长的正方形OBCD的四个顶点，两动点P、Q同时从点A出发在四边形ABCD上运动，其中动点P以每秒个单位长度的速度沿运动后停止；动点Q以每秒2个单位长度的速度沿运动，AO₁交轴于E点，P、Q运动的时间为（秒）．