中考数学模拟卷
1.![]() 的相反数是 ,
的相反数是 , ![]() 的绝对值是 ,
的绝对值是 , ![]() 的倒数是 .
的倒数是 .
2.![]() ,
,![]() .3.将用科学记数法表示为
.
.3.将用科学记数法表示为
.
4.用计算器计算:sin25°≈ ,![]() . (保留4个有效数字)
. (保留4个有效数字)
 5.小明五次测试成绩如下:91、89、88、90、92,则这五次测试成绩的平均数是 ,方差是 。
5.小明五次测试成绩如下:91、89、88、90、92,则这五次测试成绩的平均数是 ,方差是 。
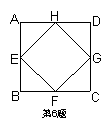
6.如图,正方形ABCD的周长为16cm,顺次连接正方形ABCD各边
的中点,得到四边形EFGH,则四边形EFGH的周长等于 cm,
四边形EFGH的面积等于 cm2.
7.10张卡片分别写有0至9十个数字,将它们放入纸箱后,任意摸出一张,
则P(摸到数字3)= ,P(摸到奇数)= .
8.在下列实数中,无理数是 【 】A、7 B、0 C、![]() D、
D、![]()
9.将100个数据分成8个组,如下表:
| 组号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 频树 | 11 | 14 | 12 | 13 | 13 | x | 12 | 10 |
则第六组的频数为 【 】 A、12 B、13 C、14 D、15
13.如图,已知AB∥CD,直线![]() 分别交AB、CD于点E、F,EG平分∠BEF,若∠EFG=40°,则∠EGF的度数是
【 】 A、60° B、70° C、80° D、90°
分别交AB、CD于点E、F,EG平分∠BEF,若∠EFG=40°,则∠EGF的度数是
【 】 A、60° B、70° C、80° D、90°

14.如图,等腰三角形ABC中,AB=AC,∠A=44°,CD⊥AB于D,则∠DCB等于
A、44° B、68° C、46° D、22° 【 】
15.如图,等腰梯形ABCD中,AB∥DC,AD=BC=8,AB=10,CD=6,则梯形ABCD的面积是
【 】 A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
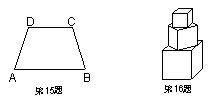
16.若干个正方体形状的积木摆成如图所示的塔形,平放于桌面上,上面正方体的下底四个顶点是下面相邻正方体的上底各边中点,最下面的正方体棱长为1,如果塔形露在外面的面积超过7,则正方体的个数至少是 【 】 A、2 B、3 C、4 D、5
17.某水电站的蓄水池有2个进水口,1个出水口,每个进水口进水量与时间的关系如图甲所示,出水口出水量与时间的关系如图乙所示.已知某天0点到6点,进行机组试运行,试机时至少打开一个水口,且该水池的蓄水量与时间的关系如图丙所示:
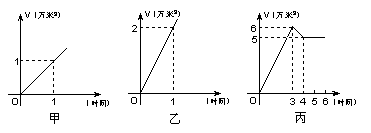
给出以下3个判断:
①0点到3点只进水不出水;②3点到4点,不进水只出水;③4点到6点不进水不出水. 则上述判断中一定正确的是 【 】 A、① B、② C、②③ D、①②③
18.化简:(1)![]() (2)
(2)![]()
19.(1)![]() (2)
(2)![]()
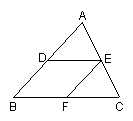 20. 如图,在
20. 如图,在![]() 中,点
中,点![]() 、
、![]() 、
、![]() 分别在
分别在![]() 、
、![]() 、
、![]() 上,
上,![]() ,
,![]() ,
,
且![]() 是
是![]() 的中点.求证:
的中点.求证:![]()
 21. 如图,已知
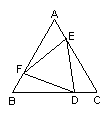
21. 如图,已知![]() 为等边三角形,
为等边三角形,![]() 、
、![]() 、
、![]() 分别在边
分别在边![]() 、
、![]() 、
、![]() 上,且
上,且![]() 也是等边三角形.(1)除已知相等的边以外,请你猜想还有哪些相等线段,并证明你的猜想是正确的;(2)你所证明相等的线段,可以通过怎样的变化相互得到?写出变化过程.
也是等边三角形.(1)除已知相等的边以外,请你猜想还有哪些相等线段,并证明你的猜想是正确的;(2)你所证明相等的线段,可以通过怎样的变化相互得到?写出变化过程.
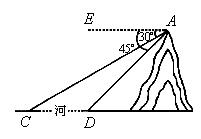
22.如图,河旁有一座小山,从山顶A处测得河对岸点C的俯角为30°,测得岸边点D的俯角为45°,又知河宽CD为50米。现需从山顶A到河对岸点C拉一条笔直的缆绳AC,求缆绳AC的长(答案可带根号)。
23. 某中学七年级有6个班,要从中选出2个班代表学校参加某项活动,七(1)班必须参加,另外再从七(2)至七(6)班选出1个班.七(4)班有学生建议用如下的方法:从装有编号为1、2、3的三个白球![]() 袋中摸出1个球,再从装有编号为1、2、3的三个红球
袋中摸出1个球,再从装有编号为1、2、3的三个红球![]() 袋中摸出1个球(两袋中球的大小、形状与质量完全一样),摸出的两个球上的数字和是几,就选几班,你人为这种方法公平吗?请说明理由.
袋中摸出1个球(两袋中球的大小、形状与质量完全一样),摸出的两个球上的数字和是几,就选几班,你人为这种方法公平吗?请说明理由.
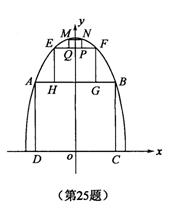 25.为了参加市科技节展览,同学们制造了一 个截面为抛物线形的隧道模型,用了三种正方形的钢筋支架.在画设计图时,如果在直角坐标系中,抛物线的函数解析式为
25.为了参加市科技节展览,同学们制造了一 个截面为抛物线形的隧道模型,用了三种正方形的钢筋支架.在画设计图时,如果在直角坐标系中,抛物线的函数解析式为![]() ,正方形ABCD的边长和正方形EFGH的边长之比为5:1,求:(1)抛物线解析式中常数
,正方形ABCD的边长和正方形EFGH的边长之比为5:1,求:(1)抛物线解析式中常数![]() 的值;(2)正方形MNPQ的边长.
的值;(2)正方形MNPQ的边长.
26.某通讯器材公司销售一种市场需求较大的新型通讯产品.已知每件产品的进价为40元,每年销售该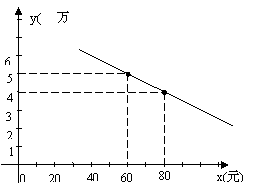 种产品的总开支(不含进价)总计120 万元.在销售过程中发现,年销售量y(万件)与销售单价x(元)之问存在着如图所示的一次函数关系.
种产品的总开支(不含进价)总计120 万元.在销售过程中发现,年销售量y(万件)与销售单价x(元)之问存在着如图所示的一次函数关系.
⑴求y关于x的函数关系式;
⑵试写出该公司销售该种产品的年获利z(万元)关于销售单价x(元)的函数关系式(年获利=年销售额一年销售产品总进价一年总开支).当销售单价x为何值时,年获利最大?并求这个最大值;
⑶若公司希望该种产品一年的销售获利不低于40万元,借助⑵中函数的图象,请你帮助该公司确定销售单价的范围.在此情况下,要使产品销售量最大,你认为销售单价应定为多少元?
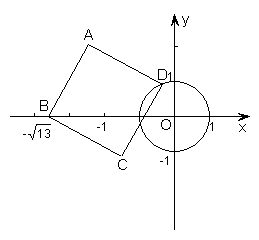
27. 已知⊙![]() 的半径为1,以
的半径为1,以![]() 为原点,建立如图所示的直角坐标系.有一个正方形
为原点,建立如图所示的直角坐标系.有一个正方形![]() ,顶点
,顶点![]() 的坐标为(
的坐标为(![]() ,0),顶点
,0),顶点![]() 在
在![]() 轴上方,顶点
轴上方,顶点![]() 在⊙
在⊙![]() 上运动.
上运动.
(1)当点![]() 运动到与点
运动到与点![]() 、
、![]() 在一条直线上时,
在一条直线上时,![]() 与⊙
与⊙![]() 相切吗?如果相切,请说明理由,并求出
相切吗?如果相切,请说明理由,并求出![]() 所在直线对应的函数表达式;如果不相切,也请说明理由;
所在直线对应的函数表达式;如果不相切,也请说明理由;
 (2)设点
(2)设点![]() 的横坐标为
的横坐标为![]() ,正方形
,正方形![]() 的面积为
的面积为![]() ,求出
,求出![]() 与
与![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的最大值和最小值.
的最大值和最小值.