专题复习----直线形1
1.
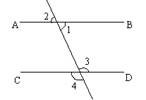如图，能判定AB//CD的条件是：
A．∠ 1＝∠4 B．∠4＋∠2＝1800
C．∠2≠∠4 D．∠3＝∠2
2. 两个角的一边在同一直线上，另一边相互平行，则这两个角的关系是：
A．相等 B．互补 C．相等或互补 D．相等且互补
3. 等腰三角形中两边长为5cm和2cm，它的周长是：
A．12㎝ B．9㎝ C．7㎝ D．9㎝或12㎝
4.
下列每组图形中，同组的两个图形必定相似的是：
A．两个等腰三角形 B．两个矩形 C．两个等腰梯形 D．两个正方形
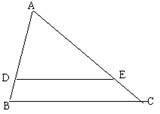
5. 如图△ABC中，DE//BC，AD＝2DB，
则DE：BC＝（ ）
A．1：2 B．2：3
C．1：3 D．4：9
6. 一个三角形的三个内角中，至少有：
A．一个锐角 B．两个锐角 C．一个直角 D．一个钝角
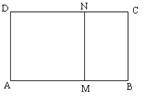
7. 如图，矩形长AB＝4，宽BC＝3，MNCB与原矩形相似，则它的周长是：
A．
B．
C．19
D．7
8. 下列各命题中，能判定两个三角形相似的有：
①两个全等三角形②两个直角三角形③有一个角相等的两个等腰三角形④周长的比等于底边的比的两个等腰三角形
A．1个 B．2个 C．3个 D．4个
9. 平行四边形一边长为14，其两条对角线长只可能是：
A．10和16 B．12与16 C．20和22 D．10与40
10.
一个角的补角等于它的5倍，这个角的余角是＿＿＿＿＿度
11. 如图，AB//CD，∠2与∠1的差是200，
则∠1＝＿＿＿＿＿度
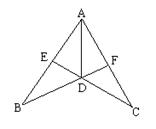
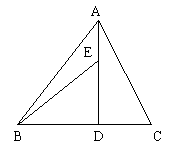
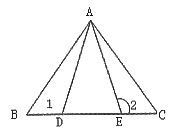
12. 如图，AB＝AC，E、F分别是AB、AC中点，共有＿＿＿对全等三角形
13. 等腰三角形一腰是底边上中线的2倍，则顶角
是＿＿＿＿＿度
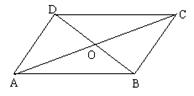
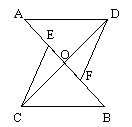
14. 如图，平行四边形ABCD对角线交点为O，与△AOD面积相等的三角形有＿＿＿个
15. 一个多边形内角和是补角和的3倍，这个多边形是＿＿＿边形
16. 顺次连结四边形各边中点得到一个菱形，这个四边形两条对角线一定＿＿＿＿＿＿＿
17. 梯形中位线长4cm，面积为2cm2，梯形的高为＿＿＿＿＿＿cm
18.
等边三角形周长为
，它的外接圆半径为＿＿＿＿＿。
19. 已知：等腰三角形底边上的高为20cm，一腰上的高为24，求底边长
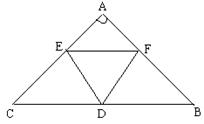
20. 如图，腰长为2cm的等腰直角△ABC中，有内接正三角形DEF，且EF//BC，BC是斜边，求△DEF的面积
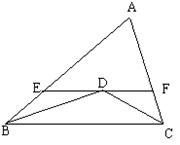
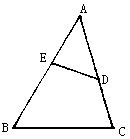
21. 如图，D是△ABC中∠ABC和∠ACB的平分线交点，过D作与BC平行的直线，分别交AB、AC于E、F，求证：EB＋FC＝EF
专题复习----直线形2
1.三条线段的比为下列四种情况，以这三条线段为边能组成三角形的是 [ ]
A. 8∶4∶3 B. 7∶5∶12 C. 4∶5∶6 D. 6∶8∶15
2.如果一个等腰三角形的一腰是顶角平分线的二倍，那么这个三角形必有一个内角等于 [ ]
A. 120° B. 90° C. 60° D. 45°
☆3.在ΔABC中，a、b、c表示三边长且
则此三角形是 [ ]
A. 等腰三角形 B. 等边三角形 C. 直角三角形 D. 钝角三角形
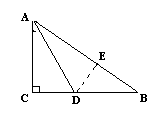4.如图，在ΔABC中，∠C＝90°，∠A的平分线交BC于D，BC＝21cm，BD∶DC＝4∶3，则点D到AB的距离为[ ]
A. 7cm B. 8cm C. 9cm D. 10cm
5.下列几种三角形中，不是轴对称图形的是[ ]
A. 有两个内角相等的三角形
B. 有两个内角为60°的三角形
C. 有一个内角是30°的直角三角形
D. 有一个内角是45°的直角三角形
6.在ΔABC中，若AB＝3，BC＝7，那么边CA的取值范围是__________．
7.在ΔABC中，若∠C＝80°，∠A＝3∠B，则∠A＝_____，∠B＝_______．
8.等腰三角形的一个外角等于140°，那么它的顶角为__________．
9.等边三角形，一边的中点到另一边的距离为3cm，则此三角形的高为_______cm．
___________________．
11、角、直角三角形、线段、等腰三角形中，轴对称图形有______________________。
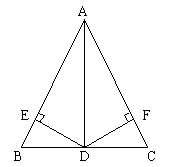
12. △ABC中，AD平分∠BAC，BD＝CD，DE⊥AB，DF⊥AC。
求证：EB＝FC
13. 如图，∠C＝90°，∠B＝30°，AD是Rt△ABC的角平分线。
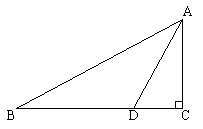求证：BD＝2CD
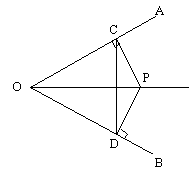14. 已知：P是∠AOB平分线上的一点，PD⊥OB，PC⊥OA，垂足分别为C、D。
求证：（1）OC＝OD；
（2）OP是CD的垂直平分线。
15、如图所示，等腰△ABC的顶角
，底边BC=6，边AC的垂直平分线交BC于D，求AD的长。
16、如图所示，已知△ABC中，AD是
A的平分线，
，求证：
。
17、如图所示，△ABC中，
。求证：
。
专题复习----直线形3
1. 设M表示直角三角形，N表示等腰三角形，P表示等边三角形，Q表示等腰直角三角形，则下列四个图中，能表示他们之间关系的是（ ）
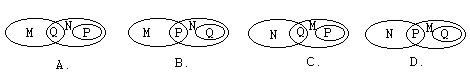
2. 具有下列条件的两个等腰三角形，不能判断它们全等的是（ ）
A. 顶角、一腰对应相等 B. 底边、一腰对应相等 C. 两腰对应相等 D. 一底角、底边对应相等
3. △ABC中，∠A：∠B：∠C=1：2：3，CD⊥AB于点D，若BC=a，则AD等于（ ）
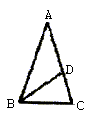
4、如图，△ABC中，AB=AC，点D在AC边上，且BD=BC=AD，则∠A的度数为（ ）
A. 30° B. 36° C. 45° D. 70°
☆5. 等腰三角形一腰上的高与底边所成的角等于（ ）
A. 顶角的一半
B. 底角的一半
C. 90°减去顶角的一半 D. 90°减去底角的一半
6. 等腰三角形中的一个内角为50°，那么它的底角是（ ）
A. 50° B. 130° C. 65° D. 50°或65°
7、如图所示，AB=AC，BD=CE，
。则图中全等的三角形共有（ ）
A. 1对 B. 2对 C. 3对 D. 4对
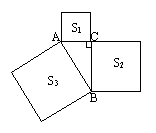
8. 如图，△ABC中，∠ACB＝90°，以△ABC的各边为边在△ABC外作三个正方形，S1、S2、S3分别表示这三个正方形的面积，S1＝81，S3＝225，则S2＝__________。
9. 等腰三角形的腰长为2cm，面积等于1cm2，则它的顶角的度数为___________。
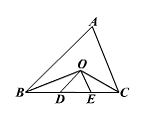
10. 已知，如图，O是△ABC的∠ABC、∠ACB的角平分线的交点，OD∥AB交BC于D，OE∥AC交BC于E，若BC＝10cm，则△ODE的周长___________。
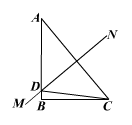11. 如图，在Rt△ABC中，∠B＝90°，∠A＝40°，AC的垂直平分线MN与AB相交于D点，则∠BCD的度数是___________。
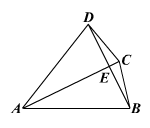12. 如图，在四边形ABCD中，对角线AC与BD相交于点E，若AC平分∠DAB，且AB＝AC，AC＝AD，有如下四个结论：①AC⊥BD；②BC＝DE；③∠DBC＝
∠DAB；④△ABC是正三角形。请写出正确结论的序号______________________
（把你认为正确结论的序号都填上）。
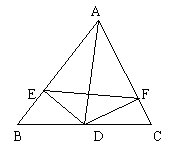
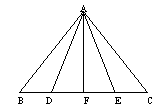
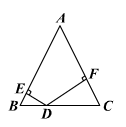13、已知：如图，D是等腰△ABC底边BC上一点，它到两腰AB、AC的距离分别为DE、DF。当D点在什么位置时，DE＝DF？并加以证明。
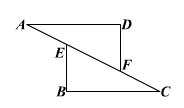
14、如图，在△AFD和△BEC中，点A、E、F、C在同一直线上，有下面四个论断：AD＝CB；（2）AE＝CF；（3）∠B＝∠D；（4）AD∥BC。请用其中三个作为条件，余下一个作为结论，编一道数学问题，并写出解答过程。
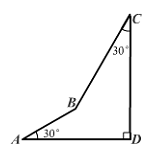15、如图，AD⊥CD，AB＝10，BC＝20，∠A＝∠C＝30°，求AD、CD的长。
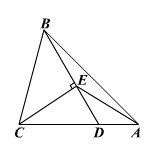
16、如图，△ABC中，D为AC上一点，CD＝2DA，∠BAC＝45°，∠BDC＝60°，CE⊥BD，E为垂足，连结AE。
（1）写出图中所有相等的线段，并加以证明；
（2）图中有无相似三角形？若有，请写出一对；若没有，请说明理由；
（3）求△BEC与△BEA的面积之比。
专题复习----直线形4
1. 已知△ABC的三边长分别是3cm、4cm、5cm，则△ABC的面积是（ ）
A. 6cm2 B. 7.5cm2 C. 10cm2 D. 12cm2
2. 下列判断正确的是（ ）
A. 有两边和其中一边的对角对应相等的两个三角形全等
B. 有两边对应相等，且有一角为30°的两个等腰三角形全等
C. 有一角和一边对应相等的两个直角三角形全等 D. 有两角和一边对应相等的两个三角形全等
3. 在平面直角坐标系xOy中，已知A（2，2），在y轴上确定点P，使△AOP为等腰三角形，则符合条件的点P共有（ ）
A. 2个 B. 3个 C. 4个 D. 5个
4. 到△ABC的三个顶点距离相等的点是△ABC的（ ）
A. 三边中线的交点 B. 三条角平分线的交点 C. 三边上高的交点 D. 三边中垂线的交点
5. 角平分线的尺规作图，其根据是构造两个全等三角形，由作图可知：判断所构造的两个三角形全等的依据是（ ）
A. SSS B. ASA C. SAS D. AAS
6. 三角形两边分别为3和7，第三边为偶数，则第三边是_________
7. 在
中，
，则
_______
8. 中，
，
和
的平分线BD和CE相交于点M，则
＝___________
9、如图所示，AD=AE，1=2，BD=CE，则有
__________，理由是_______________。
10. 如图所示，沿AM折叠，使D点落在BC上的N点处，如果AD=7cm，DM=5cm，
，则AN=___________cm，NM=________cm，
__________；
11. 如图所示，
，则D=_______，EAD=_____________；
二. 解答题
1. 如图，AE＝BF，AD＝BC，DF＝CE，求证：AD//CB
2、如图所示，在等边△ABC中，D、F分别为CB、BA上的点，且CD=BF，以AD为边作等边三角形ADE。求证：
（1）
；
（2）四边形CDEF为平行四边形。
3、如图所示，Rt△ABC中，∠C=90°，DEFG是△ABC的内接正方形。求证：EF2=AE·FB。
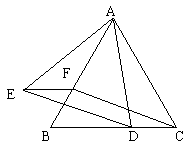
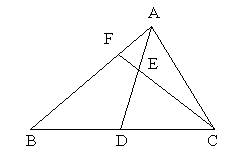
4. 如图所示，△ABC中，D是BC中点，E是AD上一点，CE的延长线交AB于F。求证：AE：ED=2AF：FB。
专题复习----直线形5
1. 两条对角线互相平分的四边形是____________________；
2. 两条对角线_________________的四边形是菱形；
3. 两条对角线_________________的四边形是矩形；
4. 两条对角线_________________的四边形是正方形；
5. 顺次连结四边形各边的中点，所得的四边形是_________________；
6. 顺次连结对角线互相垂直的四边形各边中点，所得的四边形是_____________；
7. 顺次连结对角线相等的四边形各边中点，所得的四边形是_________________；
8. 四边形四个内角的比是1：2：3：4，那么这四个角的度数分别是___________；
9. 一个多边形的每一个内角都等于144°，那么这个多边形是______________；
10. 平行四边形两邻边长分别为6cm和8cm，夹角为60°，它的面积为_________
；
11. 下列几组图形必相似的是（ ）
A. 各有角是40°的两个等腰三角形
B. 两边之比都是2：3的两个直角三角形
C. 各有一个角是100°的两个等腰三角形
D. 各有两条边成比例且有一个角相等的两个三角形
12、如图，由下列条件不能判定△ABC与△ADE相似的是（ ）
A. B. ∠B＝∠ADE
C. ∠C＝∠AED D.
13. 一个五边形的边长分别为1、2、3、4、5，另一个和它相似的五边形的最大边长为7，
则后一个多边形的周长是（ ）
A. 27 B. 25 C. 21 D. 18
14. 如图所示，△ABC中，∠ACB=90°，D是AB中点，过D作AB的垂线交CB于E，交AC的延长线于F。
求证：CD2=DE·DF。
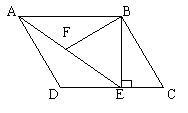
15如图所示，在平行四边形ABCD中，过点B作BE⊥CD，垂足为E，连结AE。F为AE上一点，且∠BFE=∠C。
（1）求证：△ABF∽△EAD；
（2）若AB=4，∠BAE=30°，求AE的长；
（3）在（1）、（2）的条件下，若AD=3，求BF的长。（计算结果可含根号）
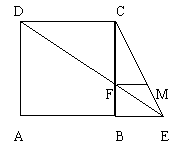
16. 如图所示，延长正方形ABCD的AB边至E，连结EC、DE，DE交BC于F，FM//BE交EC于M，求证：FB=FM。
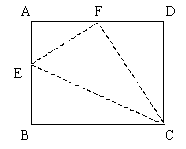17、如图所示，在矩形纸片ABCD的AB边上取一点E，使BE：EA=5：3，
，把△BCE沿折痕EC向上翻折，若点B恰好落在AD上，设这个点为F，求AB、BC的长。