初三数学毕业班第一次月考

初三数学毕业班第一次月考

数学试题

题号	一	二	三	四	五	六	七	八	九	总分
得分

一、选择题（本题共10小题，每小题4分，共40分）

（将唯一正确选项前的字母填入下表内）

题号	1	2	3	4	5	6	7	8	9	10
答案

1、顺港中学先举办了一次田径运动会，九（1）班有8名同学参赛，又举办了一次球类运动会，九（1）班有12名同学参赛，两次运动会都参赛的有3人，九（1）班共有（　　 ）名同学参赛。

A、15　　　　  B、16　　 　　　C、17　　　　  D、18

2、如果一次函数y＝kx＋b的图象不经过第三象限，也不经过原点，那么k 、b 的取值范围是（　　）

A、k＞0 且 b ＞0　　　　　  B、k＞0且　b ＜0

C、k＜0且  b＞ 0　　　　　  D、k＜0且b＜ 0

3、若一圆锥的母线长是它底面圆半径的3倍，则它的侧面展开图的园心角是（　　）

A、180°　　 B、135°C、120°　　　 D、90°

4、下面四个图形每个均由六个相同的小正方形组成，折叠后不能围成正方体的是（　　 ）

　

5、下列英文大写字母中既是轴对称图形，又是中心对称图形的是（　　 ）

A、E 　　 B、M　 C、N　D、H

6、如果要用正三角形和正方形两种图形进行密铺，那么至少需要（　　 ）

A、三个正三角形，两个正方形。　　 B、两个正三角形，三个正方形

C、两个正三角形，两个正方形。　　 D、三个正三角形，三个正方形

7、在直角坐标系中，横纵坐标都是整数的点称为整点，那么在反比例函数y＝的图像上，整点有（　　 ）

A、2个　　　　B、4个　　　 C、6个　　　　  D、8个

8、墨尔本与北京的时差是＋2h(即同一时刻墨尔本时间比北京时间早2h)班机从墨尔本飞到北京需要12h ,若乘客从墨尔本8：00（当地时间）起飞的航班，到达北京机场时，当地时间是（　　  ）

A、15：00　　 B、18：00　　　C、20：00　　　D、22：00

9、A、B、C、D、E五支球队进行单循环比赛，（每两支球队间都要进行一场比赛），当比赛进行到一定阶段时，统计A、B、C、D、四个球队已经赛过的场数，依次为A队4场，B队3场，C队2场，D队1场，这时E队赛过的场数是（　　　）
　A、4　　　　  B、3　　　　  C、2　　　　　 D、1　

10、若等腰梯形的三边长分别是3、4、11，则这个等腰梯形的周长为（　　　）

A、21　　　　 B、29　　　C、21或29　　　　D、21或22 或29

二、填空题（本题共6小题，每小题4分，共24分）

1、请你写出函数y＝(x＋1)²与y＝2x²＋1具有的一个共同性质_______________________

______________________________________________________________________

2、若数据3，2，3，x,3的平均数与众数相等，则x＝______________________________

3、已知实数x、y满足x²＋4xy＋4y²＋x＋2y－6＝0,则实数x＋2y的值为_______________

4、点A（－2，a） ，B（－1，b）,C(3,c)在双曲线y＝(k＜0）上，则a、b、c的大小关系为___________________________

5、考查下列式子，归纳规律并填空：

　　　　 1＝（－1）²×1

　　　　 1－3＝（－1）³×2

　　　　 1－3＋5＝（－1）⁴×3

　　　……　　……

1－3＋5－7＋…＋（－1）^n＋1×(2n－1) ＝_____________________________

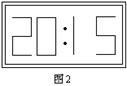6、在平面镜里，看到背后墙上电子钟示数如图所示，这是的实际时刻应该是____________

三、（12分）

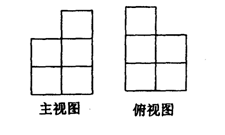
　　由一些大小相同的小正方体组成的简单几何体的主视图和俯视图（如图所示）①请你画出这个简单几何体的一种左视图。②若组成这个几何体的小正方体的块数为a ,请你写出a的所有可能值。

四、（12分）

操作设计

1、如图①是一个直角三角形纸片，要求剪一次，得到两个等腰三角形纸片，应怎样剪，画出裁剪线。

2、如图②是一块锐角三角形纸片，要求剪三次，得到三个等腰三角形纸片，应怎样剪，画出裁剪线。

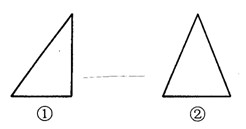
五、(12分)某商贩如果将进货单价为8元的商品按每件10元出售，每天可销售100件，现在他采用提高售货价减少进货量的办法增加利润。已知这种商品每涨价1元，其销售量就要减少10件。

①当每件商品涨价3元时，每天可销售商品多少件？所获利润为多少元？

②他将售出价定为多少元时，才能使每天所获利润最大？并求出最大利润。

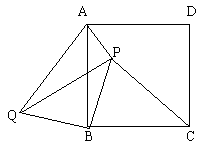
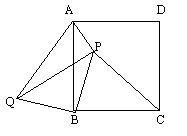
六、（10分）如图，P是正方形ABCD内一点，PA：PB：PC＝1：2：3将△PBC绕点B按逆时针方向旋转90°到△QAB的位置。

①求PQ：PB的值

②求∠APB的度数　　　　　　　　　　　　　　　　 

　　　　　　　　　　　　　　　　 　　　　　　

七、（10分）某影碟出租店开设两种租碟方式：一种是零星租碟，每张收费1元，另一种是会员卡租碟，办卡费每月12元，租碟费每张0.4元,小王经常来该店租碟,若每月租碟数量为x张。

①写出零星租碟方式应付额y₁（元)与租碟数x（张）之间函数关系式。

②写出会员卡租碟方式应付额y₂（元)与租碟数x（张）之间函数关系式。

③小王选择哪种租碟方式更合算？

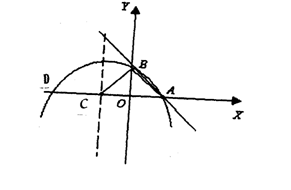
八、（10分）如图抛物线与直线y＝k(x－2)都经过坐标轴的正半轴上A、B两点，该抛物线的对称轴为x＝－与x轴相交于点C，且∠ABC＝90°

求直线AB和抛物线的解析式

　　　　　　　　　　　　　　　　　　　　 

　　　　　　　　　　　　 

九、（10分）一个家庭有3个孩子

①有这个家庭有3个男孩的概率

②有这个家庭有2个男孩和1个孩的概率

③有这个家庭有至少有一个男孩的概率

十、（10分）阅读材料，解答问题

父亲和儿子同时出去晨练，如图，实线表示父亲离家的路程y(m)与时间x(h)的函数图象，虚线表示儿子离家的路程y(m)与时间x(h)的函数图象，由图可知，他们在出发10min时相遇一次，此时离家400m，晨练了30min，他们同时到家，根据阅读材料给你的启示，利用指定的直角坐标系，或用其他方法解答问题

一巡逻艇和一货轮同时从A港口前往相距100km的B港口；巡逻艇和货轮的速度分别为100km/n和20kn/n,巡逻艇不停地往返于A、B两港口巡逻，（巡逻艇调头时间忽略不计）。

①货轮从A港口出发以后直到B港口与巡逻艇一共相遇了几次？

②出发多长时间巡逻艇与货轮第三次相遇？此时离A港口多少千米？

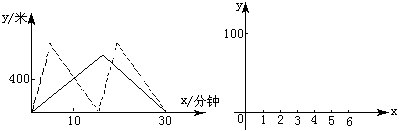
阅读下面材料：“父亲和儿子同时出去晨练.如图，实线表示父亲离家的路程y(米)与时间x(分钟)的函数图像；虚线表示儿子离家的路程y(米)与时间x(分钟)的函数图像.由图像可知，他们在出发10分钟时第一次相遇，此时离家400米；晨练了30分钟，他们同时到家.”

　　根据阅读材料给你的启示，利用指定的直角坐标系(如图)或用其它方法解答问题：

　　一巡逻艇和一货轮同时从A港口前往相距100千米的B港口，巡逻艇和货轮的速度分别为100千米/时和20千米/时，巡逻艇不停地往返于A、B两港口巡逻(巡逻艇调头的时间忽略不计).

　　(1)货轮从A港口出发以后直到B港口与巡逻艇一共相遇了几次？

　　(2)出发多少时间巡逻艇与货轮第三次相遇？此时离A港口多少千米？

　　

7．下面四个图形每个均由六个相同的小正方形组成，折叠后能围成正方体的是（　　）

（Ａ）　　　　　　　（Ｂ）　　　　　　　 （Ｃ）　　　（Ｄ）

4. 如图所示，P是正方形ABCD内一点，PA：PB：PC=1：2：3，将△PBC绕点B按逆时针方向旋转90°到△QAB的位置。

　　（1）求PQ：PB的值；

　　（2）求的度数。