平移问题

平移问题

例1：抛物线与x轴交于(x₁，0)，(x₂，0)两点，已知x₁x₂＝x₁＋x₂＋49，要使此抛物线经过原点，应将它向　　平移　　 个单位。

例2：已知二次函数，怎样平移这个函数的图象，才能使它经过(0，0)、(1，6)两点，写出平移后的二次函数的解析式，并证明新函数的图象必与x轴有两个交点。

例3：已知抛物线的对称轴是直线x＝2，且它的最高点在直线上。

(1)求这条抛物线的解析式；

(2)不改变抛物线的对称轴，将抛物线上下平移，设平移后抛物线的顶点为C，与x轴的两个交点为A(，0)，B(，0)，以点C到x轴的距离为直径的圆的面积为S，且，求平移后抛物线的解析式。

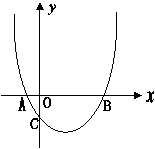
例4：如图，抛物线与x轴交于A、B两点，顶点为C，且∠ACB＝90⁰，求平移抛物线后，使得∠ACB＝60⁰时的解析式。

例5：《理科考试研究》2001.4、P10：已知抛物线C1与抛物线C2关于x轴对称，且抛物线C1的解析式是： 。①写出抛物线C1的开口方向、顶点坐标、对称轴及抛物线C2的解析式；②证明抛物线C1与抛物线C2有两个交点，并求出两个交点间的距离；③如果抛物线C1与抛物线C2的两交点与它们的两顶点组成一个正方形，试求a的值。

例6：如图，二次函数的图象交x轴于点A、B，交y轴于点C，当线段AB最短时，线段OC的长是 　　　　　　。