三角形的全等及其应用
利用全等三角形,我们可以得到有关角平分线、线段的垂直平分线、等腰三角形的许多重要性质,在本讲中将直接利用这些性质.
借助于全等三角形的知识,我们可以研究很多关于角和线段相等及不等问题、关于直线平行与垂直问题.
例1 如图所示.∠1=∠2,∠ABC=∠DCB.求证:AB=DC.
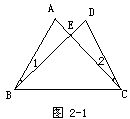
例2 如图所示.△ABC是等腰三角形,D,E分别是腰AB及AC延长线上的一点,且BD=CE,连接DE交底BC于G.求证:GD=GE.
例3 如图所示.在等边△ABC中,AE=CD,AD,BE交于P点,BQ⊥AD于Q.
求证:BP=2PQ.
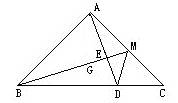
例4 如图2-6所示.∠A=90°,AB=AC,M是AC边的中点,AD⊥BM交BC于D,交BM于E.求证:∠AMB=∠DMC.
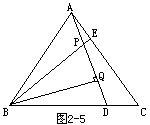
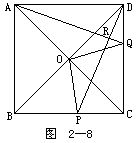
例5 如图2-8所示.正方形ABCD中,在边CD上任取一点Q,连AQ,过D作DP⊥AQ,交AQ于R,交BC于P,正方形对角线交点为O,连OP,OQ.求证:OP⊥OQ.
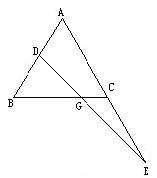
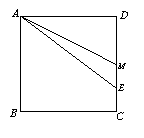
例6 如图2-9所示.已知正方形ABCD中,M为CD的中点,E为MC上一点,
且∠BAE=2∠DAM.求证:AE=BC+CE.
练 习
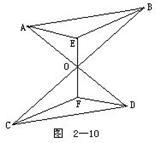
1.如图2-10所示.AD,EF,BC相交于O点,且AO=OD,BO=OC,EO=OF.
求证:△AEB≌△DFC.
2.如图2-11所示.正三角形ABC中,P,Q,R分别为AB,AC,BC的中点,M为BC上任意一点(不同于R ),且△PMS为正三角形.求证:RM=QS.
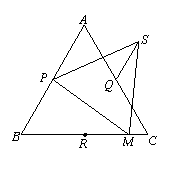
3.如图2-12所示.P为正方形ABCD对角线BD上任一点,PF⊥DC,PE⊥BC.
求证:AP⊥EF.
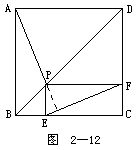
4.如图2-13所示.△ABC的高AD与BE相交于H,且BH=AC.
求证:∠BCH=∠ABC.
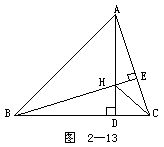
5.如图2-14所示.在正方形ABCD中,P,Q分别为BC,CD边上的点,∠PAQ=45。
求证:PQ=PB+DQ.
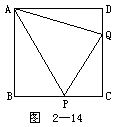
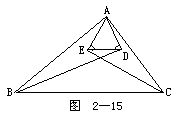
6.如图2-15所示.过△ABC的顶点A分别作两底角∠B和∠C的角平分线的垂线,AD⊥BD于D,AE⊥CE于E.求证:ED∥BC.