|
上学期九年级数学试题
一、填空题（3分×10=30分）
1.方程x2 =4x的解是 ．
2.方程
的求根公式是
．
3.在活动课上，小红已有两根长为4cm、8cm的小木棒，现打算拼一个等腰三角形，则小红应取的第三根小木棒长是_________cm．
4.用反证方法证明“在△ABC中，AB=AC，则∠B必为锐角”的第一步是假设 ．
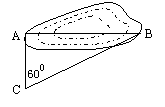
5.某风景区改造中，需测量两岸游船码头A、B间的距离，设计人员由码头A沿与AB垂直的方向前进了500m到C处，如图1所示，测得∠ACB＝600，则这两个码头间的距离AB=
m（答案可带根号）．
6.如图2，在△ABC中，已知AC=27，AB的垂直平分线交AB于点D，交AC于点E，△BCE的周长等于50，则BC= ．
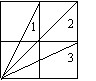
7.如图3，已知方格纸中是4个相同的正方形，则∠1＋∠2＋∠3＝ ．
8.如图4，已知∠ACB=∠BDA=900，要使△ACB≌△BDA，需要添加的一个条件是 ．
9.已知直角三角形两边x、y的长满足 ｜x2－4｜＋
＝0， 则第三边长为
．
10.欣赏下列各等式：32+42=52，102+112+122=132+142．请写出一个由7个连续正整数组成，前4个数的平方和等于后3个数的平方和的式子
．
 |
图1 图2 图3 图4
二、选择题（3分×10=30分）
11.下列方程中肯定是一元二次方程的是 ( )
A、
B、
C、
D、
12.用配方法解下列方程是，配方错误的是 （ ）
A、
B、
C、
D、
13.已知关于x的一元二次方程x2－kx－4＝0的一个根为2，则另一根是（ ）
A、4 B、1 C、2 D、－2
14.生物兴趣小组的学生，将自己收集的标本向本组其他成员各赠送一件，全组共相互赠送标本72件，若全组有x名同学，则根据题意列出方程是（ ）
A、
B、
C、
D、
15.利用13m的铁丝和一面墙，围成一个面积为20m2的长方形，墙作为长方形的长边，求这个长方形的长和宽。设长为xm，可得方程 （ ）
A、
B、
C、
D、
16.下列说法正确的是 （ ）
A、每个命题都有逆命题 B、真命题的逆命题是真命题
C、假命题的逆命题是假命题 D、每个定理都有逆定理
17.到△ABC的三边距离相等的点是△ABC的 ( )
A、三条中线的交点 B、三条角平分线的交点
C、三条高的交点 D、三条边的垂直平分线的交点
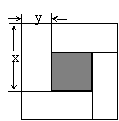18.如图5是用4个相同的小矩形与1个小正方形镶嵌而成的正方形图案，已知该图案的面积为49，小正方形的面积为4，若用x、y表示小矩形的两边长（x>y），请观察图案，指出以下关系式中不正确的是 （ ）
A、x+y=7 B、x-y=2
C、4xy+4=49 D、x2+y2=25
19.等腰三角形的腰长等于2m，面积等于1m2，则它的顶角等于（ ） 图5
A、150o B、30o C、150o或30o D、60o
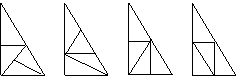20.一位园艺设计师，计划在一块有一个内角为60o的直角三角形绿化带上种植四种不同的花卉，要求种植的四种花卉分别组成面积相等，形状完全相同的几何图形图案．某同学为此提供了如图所示的四种设计方案．其中可以满足园艺设计师要求的有 （ ）
A、1种 B、2种 C、3种 D、4种 图6
三、按规定的方法解方程。（5分×4=20分）
21、
（配方法）
22、
（公式法）
23、
（分解因式法） 24、
四、作图题：（本题6分）
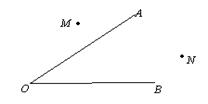
25、已知: ∠AOB, 点M、N.
求作：点P,使点P在∠AOB的平分线上,且PM=PN.
（要求：用尺规作图,保留作图痕迹,写出作法步骤）
图7
五、阅读理解题：（本题8分）
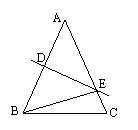
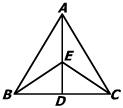26、已知：如图，D是△ABC中BC边上一点，E是AD上的一点，EB=EC，∠ABE=∠ACE，求证：∠BAE=∠CAE.
证明：在△AEB和△AEC中，
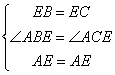
∴△AEB≌△AEC(第一步) 图8
∴∠BAE=∠CAE(第二步)
问：上面证明过程是否正确？若正确，请写出题中标出的每一步推理根据；若不正确，请指出错在哪一步？并写出你认为正确的推理过程；
六、解答题：（本题8分）
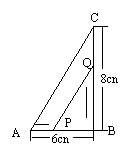27、如图所示，在△ABC中，∠B=90o，点P从A点开始沿AB边向点B以1cm/s的速度移动，点Q从点B开始沿BC边向点C以2cm/s的速度移动.如果P，Q分别从A，B同时出发，经几秒钟，使△PQB的面积等于8cm2?
图9
七、应用题：（本题8分）
28、今年，我国政府为减轻农民负担，决定在5年内免去农业税.某乡今年人均上缴农业税25元，若两年后人均上缴农业税为16元，假设这两年降低的百分率相同.(1)求降低的百分率；(2)若小红家有4人，明年小红家减少多少农业税？
八、探究题：（本题10分）
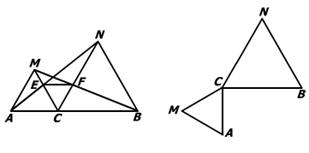29、如图10，点C为线段AB上一点，△ACM、△CBN是等边三角形，直线AN、MC交于点E，直线BM、CN交于点F。
(1)求证：AN=MN
(2)求证：△CEF为等边三角形
(3)将△ACM绕点C按逆时针方向旋转90，其他条件不变，在(2)中画出符合要求的图形，并判断（1）（2）题中的两结论是否依然成立。
（1） （2）
图10