圆周角（1）

圆周角（1）

学习目的：掌握圆周角的概念及圆周角定理

重点难点：分三种情况证明圆周角定理。

教学过程：一、复习提问：

1、　什么叫圆心角？什么是弧的度数？

2、　举例说明一个角的顶点和一个圆的位置关系有哪些可能。

圆周角的顶点在圆上，但并不是所有顶点在圆上的角都是圆周角，那么究竟什么是圆周角呢？分析顶点在圆上的角的几种情况：

　　　　　　　　　　

二、新课：

1、　圆周角：顶点在圆上，两边和圆相交的角叫做圆周角。

我们发现，实际上每一个圆周角都有一个圆心角与之对应，而建立这一联系的桥梁就是它们所共同对着的那一条弧，圆周角的度数肯定要比它所对的弧的度数小，那么究竟圆周角和它所对应的一个圆心角度数之间有什么关系呢？

在⊙O中，BC所对的圆周角是∠BAC，圆心角是∠BOC，这个图我们应怎样画呢？

圆周角定理：一条弧所对的圆周角等于它所对的圆心角的一半。

已知：⊙O中，BC所对的圆周角是∠BAC，圆心角是∠BOC

求证：∠BAC＝∠BOC

分析：如果圆心O在∠BAC的一边AB上（如图），只要利用三角形内角和定理的推论和等腰三角形的性质即可证明。如果圆心O在∠BAC的内部或外部（如图），那么只要作出直径AD，将这个角转化为上述情况的两个角的和或差即可。

证明：分三种情况讨论。

（1）如图（1），圆心O在∠BAC的一条边上。

∵OA＝OC

∴∠C＝∠BAC

∵∠BOC＝∠BAC＋∠C

∴∠BAC＝∠BOC。

（2）如图（2）中，圆心O在∠BAC的内部。作直径AD。利用（1）的结果，有

∠BAD＝∠BOD

∠DAC＝∠DOC

∴∠BAD＋∠DAC＝（∠BOD＋∠DOC）

∴∠BAC＝∠BOC

（3）如图（3）中，圆心O在∠BAC的外部。作直径AD。利用（1）的结果，有

∠DAB＝∠DOB

∠DAC＝∠DOC

∴∠DAC－∠DAB＝（∠DOC－∠DOB）

∴∠BAC＝∠BOC。

这样就得到了圆周角定理：一条弧所对的圆周角等于它所对的圆心角的一半。

例题选讲：

1、如图：OA、OB、OC都是⊙O的半径，∠AOB＝2∠BOC。

求证：∠ACB＝2∠BAC。

在⊙O中，∵∠ACB＝∠AOB，

∠BAC＝∠BOC

又∵∠AOB＝2∠BOC

∴∠ACB＝2∠BAC

课练：

（1）⊙O中，圆心角∠AOB＝100⁰，点C在劣弧AB上，点D在优弧AB上，

则∠ACB＝　　 ，∠ADB＝　　　　。

（2）如图⊙O中，若AB的度数为56⁰，则∠AOB＝　　　　，∠ACB＝　　　 。

（3）如图，AB是⊙O的直径，CD是弦，∠BDC＝25⁰，则∠BOC＝　　　 ，AC的度数为

　　　　度。

（4）等边ΔABC内接于⊙O，BD是直径，则∠BDC＝　　　 ，∠ACD＝　　　　 。若CD＝10cm，则⊙O的半径长为　　　　　  。

小结：圆周角定理：圆周角的度数等于它所对弧的度数的一半。

圆周角（2）

学习目的：掌握圆周角定理的三个推论并能运用这些知识进行有关的证明。

重点难点：推论的应用。

教学过程：一、复习提问：

1、什么是圆周角？2、圆周角度量定理的内容是什么？

图（1）同弧对圆周角；

图（2）等弧对圆周角；

图（3）（4）在等圆中，BC＝DE∠A＝∠F

二、引出新课：

推论1：同弧或等弧所对的圆周角相等；

同圆或等圆中，相等的圆周角所对的弧相等；

推论2：半圆（或直径）所对的圆周角是直角；

90⁰的圆周角所对的弦是直径。

（注意：一条弦对两个圆周角。举例：若AB为⊙O中60⁰的弧，则弦AB所对的圆周角度数为　　　　　 。）

推论3：如果三角形一边上的中线等于这边的一半，那么这个三角形是直角三角形。

例题选讲：

1、如图AD为ΔABC高，AE为ΔABC外接圆直径。求证：ABAC＝AEAD

（求解此题，注意用两种方法及AB、AC、AD、AE四条线段的关系）

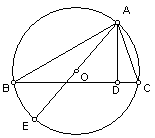2、ΔABC内接于⊙O，AO是半径，AD⊥BC于D。

求证：∠BAD＝∠OAC。

证法一：延长AO交⊙O于E，连结CE

∵AE是⊙O的直径，

∴∠ACE＝90⁰，

又∵AD⊥BC＝90⁰

∴∠B＝∠E

∴∠ACE－∠E＝∠ADB－∠B

即∠BAD＝∠OAC

证法二：如图，作OE⊥AB交⊙O于E，交AB于F。

∵OE⊥AB

∴AE＝AB

∴∠AOE的度数＝AB的度数

∴∠C的度数＝AB的度数。

∴∠AOE＝∠C

∵AD⊥BC

∴∠OFA＝∠ADC＝90⁰

∴∠OFA－∠EOA＝∠ADC－∠C

即∠FAO＝∠DAC

∴∠FAO＝∠OAD＝∠DAC＋∠OAD

∴∠BAD＝∠OAC

证法三：如图，连结OB，作OF⊥AB于F

∵AO＝OB

∴OF平分∠AOB

∴∠AOB和∠C同对AB。

∴∠C＝∠AOB，∴∠C＝∠AOF

∵AD⊥BC

∴∠AFO＝∠ADC＝90⁰

∴∠AFO－∠AOF＝∠ADC－∠C

∴∠FAO＝∠DAC

∴∠FAO＋∠OAD＝∠DAC＋∠OAD

∴∠FAD＝∠OAC

评析：①比例是关于圆周角，圆心角，直径上的圆周角，垂径定理等知识的应用题。注意所做的几种辅助线，是这几个知识点应用时常用到的。

②此例的几个证法体现了证角相等的常用方法――利用已知角的关系（角之间的相等关系，和差关系，倍分关系，互余关系，互补关系等）代换或计算。要证∠BAD＝∠CAO，作差后，即证：∠BAO＝∠CAD，然后构造直角三角形来解决是这个题的解决线索）

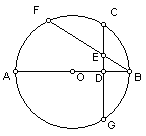
3、已知：⊙O中，AB是⊙O的直径，弦CG⊥AB于D，F是⊙O上一点且CF＝CB，BF交CG于E。求证：CE＝BE

证法一：如图，连结CB

∵AB是⊙O的直径，弦CG⊥AB

∴BC＝GB

∵CF＝BC

∴CF＝BG

∴∠C＝∠CBE

∴CE＝BE

证法二：作ON⊥BF于N，连结OE

∵AB是⊙O的直径，且AB⊥CG

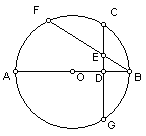
∴CB＝BG

∴CB＝CF

∴CF＝BC＝BG

∴BF＝CG

∴ON＝OD

∵∠ONE＝∠ODE＝90⁰

OE＝OE

∴ΔONEΔODE

∴NE＝DE

∵BN＝BF

CD＝CG

∴BN＝CD

∴BN－EN＝CD－DE

∴BE＝CE

证法三：如图，连结OC，BC，OE，并延长OE交BC于N。

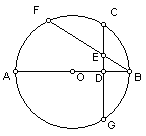∵CF＝BC

∴OC⊥BF

∵AB⊥CG

∴E是ΔOCB的垂心（垂心－三角形三条高的交点）

∴ON⊥BC

∵OC＝OB

∴ON是BC边上的中线

∴EN是BC的中垂线

∴EC＝BE

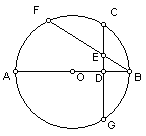
证法四：连结OC交BF于N

∵CF＝BC

∴OC⊥BF

∵AB是⊙O的直径，CG⊥AB

∴BG＝BC

∴CF＝BG＝BC

∴BF＝CG

∴ON＝OD

∵OC＝OB

∴OC－ON＝OB－OD

∵CN＝BD

又∵∠CNE＝∠BDE＝90⁰

∠CEN＝∠BED

∴ΔCNE≌ΔBDE

∴CE＝BE

评析：（1）这个题目的结论是证明线段相等，四种证法体现了证线段相等的常用方法，这四个方法是：①利用等角对等边；②利用全等三角形；③等腰三角形三线合一；④等线段减等线段。

（2）注意体会关于弧的中点问题常作的辅助线，即“弧心圆心两相连”。

（3）几何难学难就难在思路分析，请注意一题多解，它不但可以提高我们分析问题的能力，而且是串联知识，体会定理用法的好形式。

四、小结：圆周角定理及其推论。

圆周角（3）――习题课

学习目的：复习巩固圆周角定理及推论内容，并注意综合应用。

重点难点：综合应用

教学过程：一、复习提问：

1、圆周角定理的三个推论的内容及推论1的后一段话的前提条件。

2、辨别：圆周角等于圆心角的一半。

二、新课教学：

例1、已知⊙O中，OC为半径，AB、CD为弦，且OC⊥AB，垂足为N，AB、CD交于E，求证：ACBC＝CECD

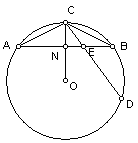
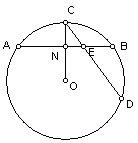
例2、已知⊙O的半径为R，弦AB长为a，弦BC∥OA，求AC长在解圆的有关问题时，常常添加辅助线构成直径所对的圆周角，以便利用直径所对的圆周角是直角的性质。

例3、已知，如图：AB是⊙O的直径，AC是弦，P是AC延长线上一点且AC＝PC，PB的延长线交⊙O于点D。求证：AC＝DC

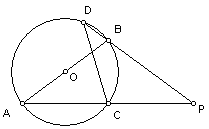
例4、ΔABC内接于⊙O，AB＝AC，弦AE交BC于D。求证：

例5、已知：AB是⊙O的直径，DM⊥AB于M，交⊙O于F，BD交⊙O于点C，AC交DM于E。求证：

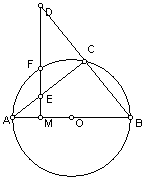
例6、若圆内接四边形的两条对角线互相垂直。

求证：自圆心到任一边的距离等于对边长的一半（变化题）

例7、已知：在⊙O中，直径AB长为10cm，弦AC长为6cm，∠ACB平分线交⊙O于D，求BC、AD和BD的长。

例8、如图弦AC＝AB，连结CA到D，使AD＝AC，连结DB并延长交圆于E。

求证：CE为圆的直径。

《海淀题链》P241例3：已知：如图，AB是半圆O的直径，C和E是半圆上两点，CD⊥AB于D，连结AE，若AC＝CE。求证：∠1＝∠2

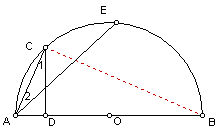解法一：连结BC，∵AB是直径，

∴∠ACB＝90⁰，

∴∠B＋∠BAC＝90⁰

∵CD⊥AB，

∴∠1＋∠BAC＝90⁰

∴∠1＝∠B

∵AC＝CE，

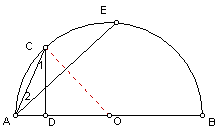∴∠B＝∠2，

∴∠1＝∠2

解法二：如图，连结OC。

∵AC＝CE，O是圆心，

∴OC⊥AE，∴∠2＋∠OCA＝90⁰。

∵CD⊥AB，∴∠1＋∠OAC＝90⁰。

∵OA＝OC，∴∠OAC＝∠OCA，

∴∠1＝∠2

点评：解法一是利用“适当作直径所对的圆周角，以及弧与圆周角互相转换思路”得到的；解法二是利用作弦心距这条常用辅助线得到的。

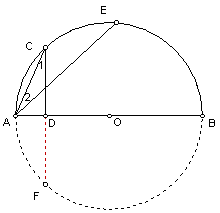解法三：如图，延长CD交另半圆于F。

∵AB是直径，CD⊥AB，

∵AC＝AF。

∵AC＝CE，

∴AF＝CE，

∴∠1＝∠2。

解法四：如图，连结BC与BE，设AE和CD交于F。

∵AB是直径，∴AE⊥BE，

∴∠ABE＋∠EAB＝90⁰，

同理∠AFD＋∠EAB＝90⁰，

∴∠AFD＝∠ABE＝∠3＋∠4。

∵AC＝CE，∴∠3＝∠4＝∠2，

∴∠AFD＝2∠2.

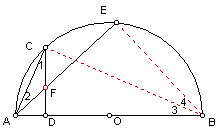∵∠AFD＝∠1＋∠2，∴∠1＋∠2＝2∠2。

∴∠1＝∠2。

《海淀题链》P255变题2：已知：如图，⊙O中弦AC⊥BD于H，若⊙O半径为2，。求DC的长。

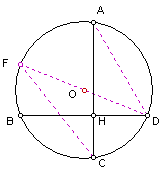解：作直径DF，连结AD，CF。

∵AC⊥BD，，

∴cot∠DAC＝，∴∠DAC＝30⁰。

∵∠F＝∠DAC，

∴∠F＝30⁰。

∵DF是直径，∴∠DCF＝90⁰，∴DC＝。

∵⊙O的半径为2，∴DF＝4，∴DC＝2。

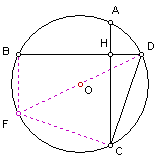
变题3已知：如图，⊙O中弦AC⊥BD于H，若⊙O半径为2，AC＝BD。求DC的长。

解：作直径DF，连结CF和BF，则∠DCF＝90⁰，FB⊥BD。

∵⊙O的半径为2，∴DF＝4。

∵AC＝BD，∴DAB＝ADC，AB＝DC。

∵AC⊥BD，

∴FB∥AC，

∴FC＝AB＝DC，

∴FC＝DC。

∵，

∴。∴DC＝。

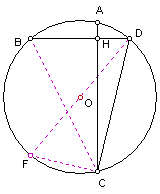变题4已知：如图，⊙O中弦AC⊥BD于H，BH：CH＝1：2，DC＝2。

求⊙O半径的长。

解：作直径DF，连结FC和BC，则∠DCF＝90⁰。

∵AC⊥BD，∠B＝∠F，∴。

∵DC＝2，∴CF＝1。

∵，

∴，

∴。

《小备课笔记》9、如图，AD是⊙O的直径，BD＝DC，AB的延长线交CD延长线于F，

CM⊥AB于M点。

求证：（相似形）

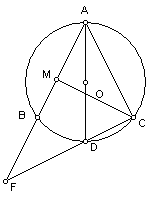
《章节讲练》P34例5：如图，在⊙O中，弦CA，DB的延长线交于F点，EF∥BC，交DA延长线于E点，求证：（相似形）

《小备课笔记》10、如图，△ABC中，AD是∠BAC的平分线，延长AD交△ABC的外接圆于E，已知AB＝2，BD＝4，BE＝5。

求AE的长。（相似形）

11、在⊙O中，CD过圆心，且CD⊥弦AB于D，过点C任作一弦CF交⊙O于F，交AB于E，若BC＝，EF＝2，求CF的长。（相似形）

1、⊙O的半径为10cm，弦AB∥CD，AB＝12cm，CD＝16cm，

求AB弦和CD弦之间的距离。（解RT△）

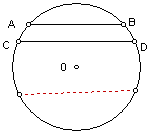解当AB和CD在圆心O的同侧时

作OM⊥AB，

∵AB∥CD，∴OM⊥CD。

∴

　

连结OA，OC，则在Rt△AMO和Rt△CNO中

∴MN＝OM－ON＝8－6＝2。

当AB和CD在圆心O的两侧时，MN＝8＋6＝14

∴弦AB和CD之间的距离等于2cm和14cm。

2、如图：△ABC内接于⊙O，若AB＝16，，求⊙O半径的长。（解RT△）

3、已知：如图，CE是⊙O的直径，弦AB⊥CE于D，

CD＝1，AB＋CD＝CE，求⊙O半径的长（解RT△）

《章节讲练》P34页例6：如图已知ΔABC是⊙O的内接正三角形，P是BC上一点。

求证：PA＝PB＋PC

《课课练》P68 3、已知：如图，弦AC⊥BD于M，OE⊥AB于E。

求证：。

P67 2、已知:如图，AB是⊙O的直径，CM⊥AB于M，交⊙O于点E，CA与⊙O交于点D，BD交CM于点N。求证：

例9、如图H为ΔABC的外心，连结AO并延长交外接圆于G点。

求证：HG与BC互相平分。

例10、如图ΔABC内接于⊙O，过O作DG⊥BC于G，交CA的延长线于P，交AB于E

求证：

《万题选》

P49：119、以ΔABC的BC边为直径的半圆，交AB于D，交AC于E，EF⊥BC于F，AB＝8cm，AE＝2cm，BF：FC＝5：1。求CE的长。

 

P53：135、已知：如图，A、B、C、D在同一圆周上，且BC＝DC＝4cm，AE＝6cm，线段BE和DE的长都是正整数，则BD的长等于多少？

131、如图，在⊙O中，直径AB、CD互相垂直，弦CH交AB于k，且AB＝10cm，CH＝8cm。求BK：AK的值。