正多边形与圆

正多边形与圆

正多边形的有关计算方法，圆及简单组合图形的周长与面积的计算方法是本节的重点，因为这些计算方法都是基本的几何计算方法，掌握这些知识，一方面可以为进一步学习打好基础，另一方面，这些知识在生产与生活中常常要用到，所以一定要掌握这些知识。

1、　圆周长，弧长

（1）　　　 设圆周长为C，半径为R，则有：C＝2 R

（2）　　　 设n⁰的圆心角所对的弧长为L，则有

2、　圆、扇形、弓形的面积。

（1）　　　 设圆的半径为R，则圆的面积为：S＝

（2）　　　 一条弧和经过这条弧的端点的两条半径所组成的图形叫扇形。

圆心角为n⁰，半径为R，弧长为的扇形面积：

（3）　　　 弓形的面积＝S_扇形±S△，当弓形面积小于半圆面积时取“－”号，大于半圆时面积取“＋”号，如图所示，

S_弓形AMB＝S_扇形OAMB－S△AOB；（如左图）

S_弓形AMB＝S_扇形OAMB＋S△AOB；（如右图）

例题选讲：

1、　如图，已知：矩形ABCD中，AD＝2AB＝2，以D为圆心DA为半径的弧交BC于F，交DC延长线于E，求阴影部分的面积。

2、　如图，已知：扇形AOB的内切⊙O₁分别切扇形半径OA、OB于D、E，且OA＝6，

⊙O₁半径为2，求图中阴影部分面积。

3、　如图，已知：△AOB中，∠O＝90⁰，OA＝OB＝2cm，以O为圆心，OA为半径画弧AB，以AB为直径作半圆，求阴影部分的面积。

4、　如图，已知正方形ABCD的边长为10cm，分别以B、D为圆心，AB为半径画弧，求阴影部分的面积。

5、　如图，已知C、D是半圆O的三等分点，圆的半径为r，求图中阴影部分的面积。

6、如图，已知：直角梯形ABCD中，∠D＝90⁰，∠A＝60⁰，AB＝4，以斜腰AB为直径的半圆切CD于E交AD于F，求圆中阴影部分的面积。

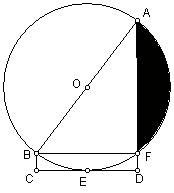
7、　如图，已知⊙O₁和⊙O₂相外切，又分别内切于⊙O，又知⊙O₁、⊙O₂、⊙O的半径分别

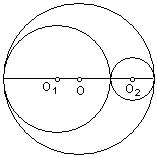为r₁、r₂、R。

求证（1）S_阴影≤S⊙O₁＋S⊙O₂；

（2）⊙O＝⊙O₁＋⊙O₂（S表示面积，表示周长）

8、　如图，已知，A、B是两圆的交点，AC是小圆的直径，D和E分别是CA和CB的延长线与大圆的交点，已知AC＝12，BE＝30，且BC＝AD，

求（1）DE的长；（2）由AC、BC与小圆劣弧AB围成的图形的面积。

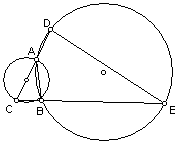
9、　已知：如图，弓形弧ACB为120⁰，它所在圆的圆心为O，CD是弓形的高，以CD为直径

作⊙O₁，求证：⊙O₁的周长＝弧AB的长。

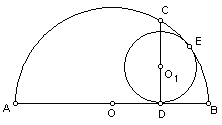10、已知：如图，AB是半圆O的直径，CD⊥AB，垂足为D，点O₁在CD上，⊙O₁与⊙O切于点E，并与AB切于点D，AB＝6cm，CD＝cm，求弧BE、弧DE和BD所围成的图形的面积。（保留两个有效数字）