九年级上数学第一次月考试卷

九年级上数学第一次月考试卷

一、选择题（每小题3分，计30分）

1、已知一个等腰三角形有一个角为50^o，则顶角是………………………（　　）

A、50^o　  B、80^o　　C、50^o或80^o　　D、不能确定

2、已知有两边为1cm和2cm，则等腰三角形周长是…………………… （　　）

  A、4cm　　B、5cm　　C、4cm或5cm　　D不能确定、

3、Rt△ABC中，∠C=90^o锐角为30^o，最短边长为5cm，则最长边上的中线是（　　）

  A、5cm　　B、15cm　　C、10cm　　D、2.5cm

4、如图∠AOP=∠BOP=15^o，PC∥OA，PD⊥OA，若PC=4，

则PD等于……（　　）

  A、4　 　 B、3　　　C、2　 　 D、1

5、关于x的一元二次方程x²-kx-7=0的一个根为x₁=1，另一根为x₂，则有… （　　）

  A、k=-6，x₂=-7　　B、k=6，x₂=7　  C、k=-6，x₂=7　　D、k=6，x₂=7

6、把方程化成一般式，则、、的值分别是……（　　）

A .　　 B.　　 C .　　 D .

7、如图，△ABC是不等边三角形，DE=BC，以D、E为两个顶点作位置不同的三角形使所作三角形与△ABC全等，这样的三角形

最多可以画出…………（　　）

A、4个　　 B、5个　　 C、6个　　 D、8个

8、△ABC中，点O为∠ABC和∠ACB角平分线交点，则∠BOC与∠A的关系是（　　）

  A、∠BOC =2∠A　　　　　　　　  B、∠BOC =180^o-∠A　

C、∠BOC =90^o+∠A　　　　　　 D、∠BOC=90⁰+∠A

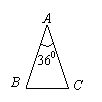9、如图，在下列三角形中，若AB＝AC，则能被一条直线分成两个小等腰三角形的是……（　　）

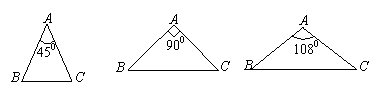（1）　　　　　 （2）　　　　　　  （3）　　　　　　  （4）

A.（1）（2）（3）　　　　　　　　　  B. （1）（2）（4）　　　　　　　

C.（2）（3）（4）　　　　　　　　　  D. （1）（3）（4）

10、某地2001年外贸收入为m亿元，2002年比2001年增加x%预计2003年比2002年增加2x%，则2003年外贸收入达到n亿元，则可以列出方程是………………………（　　）

A、m(1+x%)²=n，(m+2x)²=n　　　　　  B、(m+2x)²=n

C、m(1+x%)(1+2x%)=n　　　　　　　  D、m(1+2x)(1+2x)=n

二、填空题（每空2分，计20分,其中第16题每空1分）

11、如图，∠A=∠D=90^o，要使△ABC≌△DCB，只需再添加　　　　　 条件即可。

12、方程(x-2)²=4的根是　　　　　　　　　 。

13、如图AC、BC是△AOB的两个外角∠MOB和∠NBA的平分线，C为交点，已知，∠AOB=50^o，则

∠COB=　　　　　　　  度。

14、如图在△ABC中∠A=90^o，∠B=15^o，DE垂直平分BC，

垂足为D，交AB于E，AC=10cm，BE=　　　　  cm。

15、用反证法证明命题“三角形中，至少有一个角

不小于60^o，假设“　　　　  ”则与“　　　　　　　　  ”矛盾所以原命题正确。

16、

17、如图，为了求出湖两岸A、B两点之间的距离，观测者从测点A、B分别测得∠BAC＝90°，∠ABC＝30°，又量得BC＝160 m，

则A、B两点之间的距离为　　　　m（结果保留根号）。

18、有一个等腰三解形一腰上的高度是腰长的一半，则此等腰三角形的顶角是　　　　度。

19、一架长2.5m的梯子，斜立在一竖直的墙上，这时梯子底端距墙底端0.7m，如果梯子的顶端沿墙下滑0.4m，那么梯子底端将滑动

了　　　　  m。

三、过程题（计50分）

20、解下列一元二次方程（16分）

　 （1）4x²=x　　 　　　　　　　　　　　　(2)（配方法解）3x²-4x-6=0

　 （3）x²-2x-15=0　　　　　　  　　　　 （4）4x²-4+5=0

　　　　　　　　　　

21、（5分）如图已知∠AOB内有两点，M、N求作一点P，使点P在∠AOB两边距离相等，且到点M、N的距离也相等，保留作图痕迹并完成填空。

解：（1）连结　　　　　　  ；

作　　　　　　　 中垂线CD。

（2）作∠AOB的　　　　 OE

与CD交于点　　　　 ，

所以点　　　 就是要找的点。

22、（5分）如图在∠ABC中，∠B=30^o，AC= ，等腰直角△ACD斜边AD在AB边上，求BC的长。（提示：作AD边上的高）

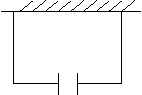23、（6分）如图，要建一个面积为130m²的仓库，仓库的一边靠墙（墙长16m），并在与墙平行的一边开一道1m宽的门。现在可围的材料为32m长的木板。求仓库的长和宽各几米？

24、（6分）关于x的一元二次方程ax²+bx+c=0中，当b²-4a≧0，方程的两个根x₁和x₂不相等或相等，而且有x₁+x₂=- ,x₁·x₂= ；当b²-4ac<0时，方程无实数解。比如方程x²-7x+12=0的两根x₁=3，x₂=4，则有b²-4ac=49-4×1×12=1>0，而且x₁+x₂=7，x₁·x₂=12，2x²+x+1=0,b²-4ac=1-4×2×1=-7<0，方程无解。根据以上情况解下列问题。已知Rt△ABC中，∠C=90^o，BC=a，AC=b，a>b，且a，b是关于x的方程x²-(m-1)x+(m+4)=0的两根，当AB=5时。

（1）求m的值；（2）求a和b

　　

25、（6分）如图△ABC中，点D在AC上，E在AB上，且AB=AC，BC=CD，AD=DE=BE。

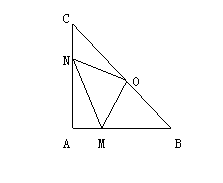（1）求证△BCE≌△DCE；　　　　　　 

　（2）求∠EDC的度数。

26、（6分）在Rt△ABC中，AB=AC，∠BAC=90^o，点O为BC的中点，在AB、AC上有两个动点M和N，在移动中保持AN=BM，请猜想△OMN的形状，并证明你的猜想。