九年级上学期期中数学综合练习题一

九年级上学期期中数学综合练习题一

一、选择题

1、下列方程是一元二次方程的是（　  ）

A、x²+3x-2y =5　  B、－2x =1　　 C、(x-1) ² +1= x²　　D、x²-8=x

2、在用配方法解方程x²-6x+1=0中，下列变形正确的是（　　 ）

A、(x-3) ²=8　 B、(x+3) ²=8 　 C、(x-3) ²=10　 D、(x+3) ²=10

3、关于的一元二次方程的一个根是0，则值为（　 ）

A、　　  B、　　　　　 C、或　　　　 D、

4、已知三角形两边长分别为2和9,第三边的长为二次方程x²-14x+48=0的一根, 则这个三角形的周长为(　 )

　A.11　　 B.17　　 C.17或19　　 D.19

5、若关于y的一元二次方程ky²-4y-3=3y+4有实根,则k的取值范围是(　 )

A.k>-　　　　 B.k≥- 且k≠0　　　C.k≥-　　　  D.k> 且k≠0

6、若则x的取值范围是　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

A. x≥　　　　B. x≤ 　　　　　　　 C. x ＞　　　　　　D. x＜

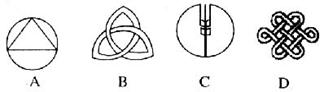
7、如图所示的几幅图中，可以旋转180°与自身重合的是（　　）

8、下列几何图形中，是中心对称图形而不是轴对称图形的是（　　）

A、线段 B、圆　　 C、矩形 D、平行四边形

9、10个人去钓鱼，共钓到3条鱼，假设每个人钓到鱼的可能性相同，那么这3条鱼由同一个人钓到的概率是（　　　 ）

（A） 　 （B） 　 （C） 　 （D）

10、“从布袋中取出一个红球的概率为0”，这句话的含义是（　　 ）

(A) 布袋中红球很少　 　 (B) 布袋中没有球　(C) 布袋中没有红球　　　(D) 不能确定

7、如图，用直角钢尺检查某一工件是否为半圆环形，根据所检查的情形，四个工件中肯定是半圆环形的是(　　)

11、在等腰△ABC中，AB=AC=2cm，若以A为圆心，1cm为半径的圆与BC相切，

则∠ABC的度数为（ 　　）

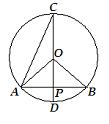A、30°　　　　 B、60°　　　　 C、90°　　　　 D、120°

12、一弦分圆周角成两部分，其中一部分是另一部分的4倍，则这条

弦所对的圆周角度数为（　　　 ）

A、36º　　 　　B、72º　 　　　 C、36º或144º　　  D、144º

13、如图，在⊙O中，P是弦AB的中点，CD是过点P的直径，

则下列结论中不正确的是（　　）

　A、AB⊥CD　 B、∠AOB =4∠ACD　 C、AD与BD这两条弧相等　D、PO =PD

14、⊙O的半径是20cm,圆心角∠AOB=120°,AB是⊙O弦,则等于(　 )

　A.25cm²　　　B.50cm²　　　 C.100cm²　　　 D.200cm²

15、圆锥的母线长5cm,底面半径长3cm,那么它的侧面展开图的圆心角是(　)

A.180°　　B.200°　　C.225°　　D.216°

二、填空题

1、方程的解是　　　　  .

2、若方程是关于x的一元二次方程，则m=　　　 。

3、已知x＝，则的值等于___________.

4、抛掷一枚变通的硬币三次，连续掷出三个正面与先掷出两个正面再掷出一个反面的概率分别是（　　）

Ａ．，　　　　　　　Ｂ．，　　　　　Ｃ．，　　　　　Ｄ．，

5、从六名同学中派两名同学去观看排球比赛，黄帅是这六名同学之一，他被派去的概率是（　　）

Ａ．　　　　　 Ｂ．　　　　　Ｃ．　　　　　Ｄ．

6、如图，等边△ABC的边BC上一点D，△ABD绕点A旋转到△ACE，

则∠DAE＝　　　　　  °

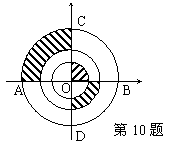7、如图，线段AB为⊙O的一条弦，OD⊥AB于D，

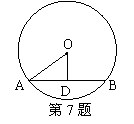且OD=8cm，AB＝12cm，则该圆的半径为　　　　　 。

　

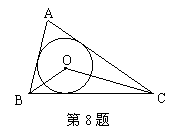
8、如图所示，⊙O为△ABC的内切圆，，，则　 ° 　

9、一个直角三角形的两条直角边长是方程的两个根，则此直角三角形外接圆的半径等于　　　　　 。

10、如图所示，三圆同心于O，AB=4cm，CD⊥AB于O，则图中阴影部分的面积为　　　　　　  。

三、解答题

1、计算

（1）（+）—（—）　　 （2）（+）÷

（3）　　　　　　　（4）

2、用适当的方法解下列方程

（1）（3x—1）²=（x+1）²　　　　　　 （2）

（3）x²—4x + 1=0　　　　　  　　　　　 （4） (x＋2)(x－5)＝1．

3、若是关于x的一元二次方程，试求：(1) m的值。

(2) 写出这个一元二次方程的一般形式.

　　　　　　　　　　　　　　　　   (这题的答案直接写在横线上,不要求说明.)

 (3)用适当的方法求出上面方程的根。

4、已知关于x的一元二次方程，其根的判别式的值等于1，求m的值及该方程的根．

解：

5、已知关于x的方程x²―(2k+1)x+4(k-)=0

(1)　求证：不论k取什么实数值，这个方程总有实数根；

（2）若等腰三角形ABC的一边长为a=4，另两边的长b、c恰好是这个方程的两个根，求△ABC的周长。

6、己知一元二次方程．

（1）若方程有两个不相等的实数根，求实数的取值范围；

（2）若方程有两个相等的实数根，求此时方程的根．

7、如图，所示的是聪聪从自已家到叔叔家,再到奶奶家的路线图.

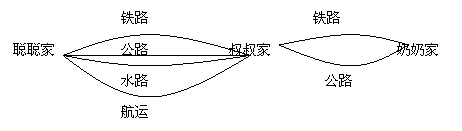从图中可以看到聪聪家到叔叔家有4条路,从叔叔家到奶奶家有2条路,你能求出从聪聪家到奶奶家始终利用一种交通工具的路线概率吗？请用树状图表示.

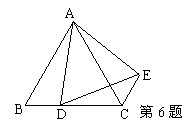
8、△ABC中，∠B＝10°，∠ACB＝20°，AB=4cm，△ABC逆时针旋转一定角度后与△ADE重合，且点C恰好成为AD中点。

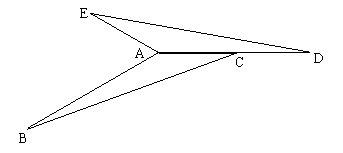（1）指出旋转中心，并求出旋转度数。

（2）求出∠BAE的度数和AE的长。

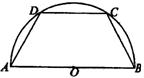
9、如图，四边形ABCD内接于半圆O，AB是直径．（1）请你添加一个条件，使图中的四边形ABCD成等腰梯形，这个条件是　　　　　 （只需填一个条件）。（2）如果CD＝AB，请你设计一种方案，使等腰梯形ABCD分成面积相等的三部分，并给予证明．

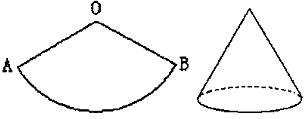
10、如图，扇形OAB的圆心角为120°，半径为6cm．

(1)请用尺规作出此扇形的对称轴(不写作法，保留作图痕迹)；

(2)若将此扇形围成一个圆锥的侧面 (不计接缝)，求圆锥的底面半径．

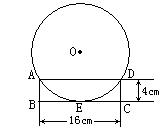11、工人师傅为检测该厂生产的一种铁球的大小是否符合要求，设计了一个如图所示的矩形ABCD工件槽，将形状规则的铁球放入槽内时，若同时具有图中所示的A、D、E三个接触点，该球的大小就符合要求。请你结合图中的数据，计算这种铁球的直径。

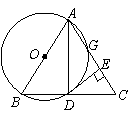12、如图，以等腰三角形的一腰为直径的⊙o交于点，交于点，连结，并过点作，垂足为．根据以上条件写出三个正确结论（除外）是：

（1）　　　　　　　　；

（2）　　　　　　　　；

（3）　　　　　　　　．

　　选择其中的一个加以证明。

13、如图所示,已知AB为⊙O的直径,C、D为圆上两点,CE⊥AB,DF⊥AB, 垂足分别为E、F,且,求证:CE=DF.

14、某商店将进价为8元的商品按每件10元售出，每天可售出200件，现在采取提高商品售价减少销售量的办法增加利润，如果这种商品每件的销售价每提高0.5元其销售量就减少10件，问应将每件售价定为多少元时，才能使每天利润为640元？

15、已知a、b均为正数。

Ⅰ）观察：①若a＋b=2，则≤1　　　　　 ②若a＋b=3，则≤

③若a＋b=6，则≤3

Ⅱ）猜想：①若a＋b=9，则≤___________,②若a＋b=m，则≤____________

Ⅲ)证明:试对猜想②加以证明.

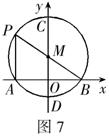16、如图7，在平面直角坐标系中，点的坐标为，⊙M与轴相交于两点，且，与轴相交于两点．

（1）请直接写出两点的坐标；

（2）若点在弧上移动（不与点重合），当点移动到

何处时，的面积最大？并求出这时的面积．

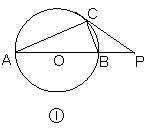
17、已知如图①，点P在⊙O外，PC是⊙O的切线，切点为C，直线PO与⊙O相交于点A、B.（1）试探求∠BCP与∠P的数量关系；（2）若∠A=30°，则PB与PA有什么数量关系？（3）∠A可能等于45°吗？若∠A=45°，则过点C的切线与AB有怎样的位置关系？（在图②上作图）（4）若∠A﹥45°，则过点C的切线与直线AB的交点P的位置将在哪里？（在图③上作图）

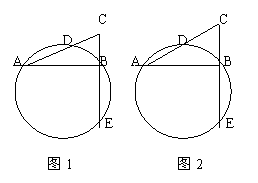
18、已知：在Rt△ABC中，D为AC的中点，⊙O经过A、D、B三点，CB的延长线交⊙O于E（如图1）；在满足上述条件下，当∠CAB的大小变化时，图形也随着改变（如图2）；在这个变化过程中，有些总保持着相等关系。

观察右边图形，连接图中已标明的两点，得到一条新线段，证明它与线段CE相等。