九年级数学测试（3）

九年级数学测试（3）

姓名　　　　　　　　  学号　　　　　　　　　

一：填空（每小题3分共21分）

1．如图，修建抽水站时，沿着倾斜角为30⁰的斜坡铺设管道，若量得水管AB的长度为80米，那么点B离水平面的高度BC的长为　　　　　　  米。（2005重庆）

2．若x=1是一元二次方程ax²＋bx－2=0的根，则a＋b=　　　　　　 。（2005辽宁）

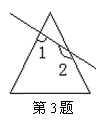
3．如图，一个顶角为40º的等腰三角形纸片，剪去顶角后，得到一个四边形，则_________　；（2004杭州）

4．方程（x－1）(x＋2)(x－3)=0的根是　　　　　　　　　　　  （2004温州）

5．三角形三内角的度数之比是1：2：3，最大边的长是8cm，则最小边的长是　　　　　 cm.

6.已知－2是方程x²－4x ＋c=0的一个根，则另一个根是　　　　　　  。

7．方程：x－2=x(x－2)的解是　　　　　　　  ；方程x²=3x的解是 　　　　　　　　　　。

二：选择（每小题3分共18分）

1．方程 x²－x=0的根是（　　  ）(2005拢南市)

　 A、x=1　 B、x=0　 C、x₁=0或x₂=1　 D、x₁=－1或x₂=1

2.等腰三角形一腰上的高与另一腰的夹角为30^o，则顶角的度数为（　　  ）(2005临沂)

  A、60^o　B、120^o 　C、60^o或150^o　　D、60^o或120^o

3．用配方法解一元二次方程x²－4x－1=0，配方后得到的方程是（　　 ）（2005辽宁）

　A、（x－2）²=1　B、（x－2）²=4　 C、(x－2)²=5　 D、(x－2)²=3

4. 如图，在△ABC中，BC = 8 cm，AB的垂直平分线交AB

于点Ｄ，交边AC于点E，△BCE的周长等于18 cm，则

AC的长等于（　　　）。

A．6 cm　　 B．8 cm　　C．10 cm　　 　　　 D．12 cm

5．把一个小球以20m/s的速度竖直向上弹出，他在空中的高度h(m)

  与时间t(s)满足关系：h=20t－5t² ,当h=20时，小球的运动时间为（　　 ）

 A、20s　 B、2s　C、(2＋2)s　 D、(2－2)s　　　  (2004河北)

6．小萍要在一幅长是90厘米、宽是40厘米的风景画四周外围，镶上一条宽度相同的金色纸边，制成一幅挂图，使风景画的面积是整个挂图面积的54%。设金色纸边的宽度是x厘米，根据题意所列方程是（　　　 ）（2004山西）

A、（90＋x）(40＋x)×54%=90×40　　B、(90＋2x)(40＋2x)×54%=90×40

C、(90＋x)(40＋2x)×54%=90×40　　 D、(90＋2x)(40＋x)×54%=90×40

三：解答题（要求写出主要的步骤共81分）

1． 用适当的方法解下列方程 (24分)

（1）x²－4x＋1=0　 (2005北京)　　　　　　　　 （2）x²＋5x＋3=0

 

（3）3x(x－1)=2－2x　　　　　　　　　　　　　　　 (4) x²=x＋56

2．某企业的年产值在两年内从1000万元增加到1210万元，求平均每年增长的百分率。

　 (2005大连) (8分)

3．已知：如图7，D是△ABC的边AB上一点，AB∥FC，DF交AC于点E，DE＝EF。

　　求证：AE＝CE。 （9分）

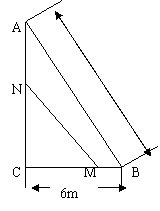4．如图，在直角ΔABC中，∠C=90^o ，BC=6m, AB=10m. 点M从B点以1m/s的速度向点C匀速移动，同时点N从C点以2m/s的速度向点A匀速移动，问几秒钟后，ΔMNC的面积是ΔABC面积的？  （10分）

5．课外植物小组准备利用学校的一块空地，开辟一个面积为130平方米的花圃（如图），打算一面利用长是15米的仓库墙面，三面利用长是33米的旧围栏，求花圃的长和宽。

 （2004南山）（10分）

6. 阅读下题及其证明过程：（10分）

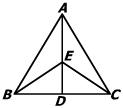
已知：如图，D是△ABC中BC边上一点，EB=EC，∠ABE=∠ACE，求证：∠BAE=∠CAE.

证明：在△AEB和△AEC中，

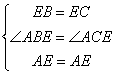
∴△AEB≌△AEC(第一步)

∴∠BAE=∠CAE(第二步)

问：上面证明过程是否正确？若正确，请写出每一步推理根据；若不正确，请指出错在哪一步？并写出你认为正确的推理过程；

8. 宏达汽车租赁公司有出租车120辆，每辆汽车的月租金为160元，出租车业务天天供不应求，为适应市场需求，公司准备适当提高日租金，经市场调查发现，一辆汽车的日租金每增加10元，每天出租的汽车相应的减少6辆，该公司的日租金提高多少元时，可使租金总收入达到19440元？（10分）