九年级数学期中试卷5
班级 姓名
一、选择题(每题3分,共30分)
1.下列说法中,错误的是( ).
A、一组对边平行且相等的四边形是平行四边形
B、两条对角线互相垂直且平分的四边形是菱形
C、四个角都相等的四边形是矩形
D、邻边相等菱形是正方形
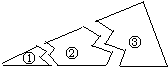
2.如图,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块完全一样形状的玻璃.那么最省事的办法是带______去配( ).
| A、① | B、② |
| D、①和③ |
 |
(第2题) (第3题)
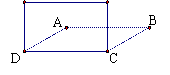
3.如图,边长为12米的正方形池塘的周围是草地,池塘边A、B、C、D处各有一棵树,且AB=BC=CD=3米.现用长4米的绳子将一头羊拴在其中的一棵树上.为了使羊在草地上活动区域的面积最大,应将绳子拴在( ).
| A、A处 | B、B处 | C、C处 | D、D处 |
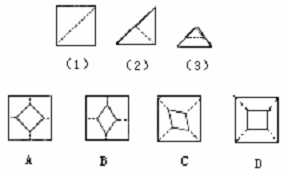 |
4.小强拿了一张正方形的纸如图(1),沿虚线对折一次得图(2),再对折一次得图(3),然后用剪刀沿图(3)中的虚线(虚线与底边平行)剪去一个角,再打开后的形状应是( ).
(第4题) (第5题 )
)
5.某风筝厂准备购进甲、乙两种规格相同但颜色不同的布料生产一批形状如图所示的风筝,点E,F,G,H分别是四边形ABCD各边的中点.其中阴影部分用甲布料,其余部分用乙布料(裁剪两种布料时,均不计余料).若生产这批风筝需要甲布料30匹,那么需要乙布料( ).
| A、15匹 | B、20匹 | C、30匹 | D、60匹 |
6.一元二次方程![]() 的解是( ).
的解是( ).
| A、 | B、 | C、 | D、 |
7.党的十六大提出全面建设小康社会,加快推进社会主义现代化,力争国民生产总值到2020年比2000年翻两番。在本世纪的头二十年(2001年~2020年),要实现这一目标,以十年为单位计算,设每个十年的国民生产总值的增长率都是x,那么x满足的方程为( ).
| A、(1+x)2=2 | B、(1+x)2=4 | C、1+2x=2 | D、(1+x)+2(1+x)=4 |
8.到△ABC的三个顶点距离相等的点是△ABC的( ).
A、三条中线的交点 B、三条角平分线的交点
C、三条高线的交点 D、三条边的垂直平分线的交点
9.关于x的一元二次方程(a-1)x2+x+a2-l=0的一个根是0.则a的值为( ).
| A、1 | B、-l | C、1 或-1 | D、 |
10.下图是由一些相同的小正方体构成的几何体的三视图.这些相同的小正方体的个数是( ).
| A、4个 | B、5个 |
| D、7个 |
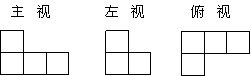 |
(第10题) (第11题) (第12题)
二、填空题(每空2分,共18分)
11.如图,若将四根木条钉成的矩形木框变形为平行四边形ABCD的形状,并使其面积为原矩形面积的一半,则这个平行四边形的一个最小内角的值等于 °.
12.如图,有一腰长为5cm,底边长为4cm的等腰三角形纸片,沿着底边上的中线将纸片剪开,得到两个全等的直角三角形纸片,用这两个直角三角形纸片拼成的平面图形中,有 个不同的四边形.
13.请写出等腰梯形ABCD(AB∥CD)特有而一般梯形不具有的三个特征:___________________;_______________________;_________________________.
14.已知等腰三角形的一边等于5,另一边等于6,则它的周长等于 .
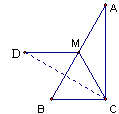
 15.如图,在RtΔABC, ∠ACB=900, ∠A<∠B,CM是斜边AB的中线,将ΔACM沿直线CM折叠,点A落在点D处,若CD恰好与AB垂直,则∠A等于 度.
15.如图,在RtΔABC, ∠ACB=900, ∠A<∠B,CM是斜边AB的中线,将ΔACM沿直线CM折叠,点A落在点D处,若CD恰好与AB垂直,则∠A等于 度.
(第15题) (第16题) (第17题)
 |
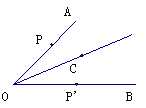
16.如图,已知点C是∠AOB的平分线上一点,点P、P’分别在边OA、OB上。如果要得到OP=OP’,需要添加以下条件中的某一个即可,请你写出所有可能的结果的序号为____________.
①∠OCP=∠OCP’ ②∠OPC=∠OP′C; ③PC=P′C; ④PP′=OC
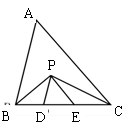
17.如图,在ΔABC中,BC=5 cm,BP、CP分别是∠ABC和∠ACB的角平分线,且PD∥AB,PE∥AC,则ΔPDE的周长是___________ cm.
18.张明同学想利用树影测量校园内的树高.他在某一时刻测得小树高为1.5米时,其影长为1.2米,当他测量教学楼旁的一棵大树影长时,因大树靠近教学楼,有一部分影子在墙上.经测量,地面部分影长为6.4米,墙上影长为1.4米,那么这棵大树高约________米.
三、解答题(第19~23题每题6分,第24题10分,第25题12分,共52分)
19.如图,点E是正方形ABCD的边CD上一点,点F是CB的延长线上一点,且EA⊥AF.
 求证:DE=BF.
求证:DE=BF.
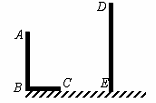
20.如图,AB和DE是直立在地面上的两根立柱.AB=5m,某一时刻AB在阳光下的投影BC=3m.
(1)请你在图中画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,请你计算DE的长.
 |
21.有一块三角形的地,现要平均分给四农户种植(即四等分三角形面积).请你在图上作出分法.(不写作法,保留作图痕迹)
 |
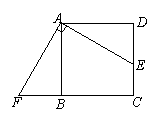
 22.用剪刀将形状如图1所示的矩形纸片ABCD沿着直线CM剪成两部分,其中M为AD的中点.用这两部分纸片可以拼成一些新图形,例如图2中的Rt△BCE就是拼成的一个图形.
22.用剪刀将形状如图1所示的矩形纸片ABCD沿着直线CM剪成两部分,其中M为AD的中点.用这两部分纸片可以拼成一些新图形,例如图2中的Rt△BCE就是拼成的一个图形.
用这两部分纸片除了可以拼成图2中的Rt△BCE外,还可以拼成一些四边形.请你试一试,把拼好的四边形分别画在图3、图4的虚框内.
23.某工厂现有80台机器,每台机器平均每天生产384件产品,现准备增加一批同类机器以提高生产总量,在试生产中发现,由于其它生产条件没变,因此每增加一台机器,每台机器平均每天将少生产4件产品.问应增加多少台机器,才可以使每天的生产总量达到30976件?
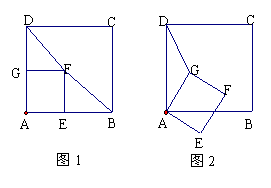
24.已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.
(1) 如图1, 连结DF、BF,若将正方形AEFG绕点A按顺时针方向旋转,判断命题:“在旋转的过程中线段DF与BF的长始终相等.”是否正确,若正确请证明,若不正确请举反例说明;
(2) 若将正方形AEFG绕点A按顺时针方向旋转, 连结DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长始终相等?并以图2为例说明理由.
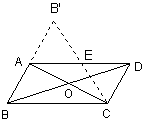
25.如图,在□ABCD的纸片中,AC⊥AB,AC与BD相交于O,将△ABC沿对角线AC翻转180°,得△AB’C.
(1)求证:以A、C、D、B’为顶点的四边形是矩形;
(2)若四边形ABCD的面积S=12cm. 求翻转后纸片重叠部分的面积,即S△ACE.
 |
 C、③
C、③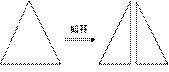 C、6个
C、6个