九年级数学月检试题卷

九年级数学月检试题卷

（总分150分，90分钟完巻）班级_________姓名________________

一、选择题：（每小题3分，共计36分）

1.代数式有意义，则x的取值范围是（　　　）

A．3<x<≤4　　　　　 B.3<x<4　　　C.3≤x≤4　　 D.3≤x≤4

2．下列四个图案中，符合右图所示的胶筒滚动后的图案是（　　 ）

3. －的结果是（　　　 ）

A.-2()　　　B.0　　　　  C.-2　　D.-2

4.分式＝0,则x的值为（　　　　）

A.2　　　　　　　B.±2　　　 C.-2　　　　  D. ±4

5.关于x的方程ax²—3x＋2＝2x² 是一元二次方程，则a的取值范围是（　　　）

　　A.a≠2　　　　B.a≠-2　　　　　 C.a≠2　　　　D.a≠±2

6.如图，A、B、C、D、四点均在⊙O上，BD的延长线与AC的延长线交于P

∠AOB=120⁰，p=20⁰,则∠ACB,∠COD的度数分别为（　　　）

　A.60⁰,20⁰　　　　B.120⁰,100⁰　　C.60⁰,80⁰　　　D.60⁰,40⁰

7.半径为5cm的⊙O中，弦AB＝5cm，则弦AB所对的圆周角为（　　　）

　 A.60⁰　　　　　　　B.30⁰　　　　　C.150⁰ 　　　　 D.30⁰或150⁰

8.CD为⊙O的直径，弦AB⊥CD于M，若CM＝12,DM＝8,则AB等于（　　）

　  A．4　　　　　 B.8　　　　 C.8　　　 D. 4

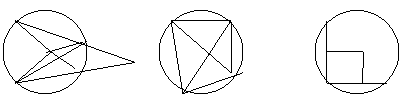
 9.⊙O上有四点A、B、C、D，则图中相等的角有（　　  ）

 A.2对　　　　　 B.3对　　　　 C.4对　　　　 D.5对

10. ⊙O上有A、B、C三点，且AB⊥BC，D、E分别为AB、BC的中点，AB＝10,则四边形BDOE的形状和面积分别是（　　 ）

 A.矩形，100, B.正方形，25　C.菱形，25　　D.任意四边形，无法计算

11.关于X的一元二次方程ax²＋6x－3＝0有两个不相等的实数根，则直线y=ax－a的图像大致是（　　  ）

　　　　　　　　　　　　

　　　　

　　　 A 　　　　　　　 B　　　　　　  C　　　　　　  D

12. ⊙O的半径为5cm,弦AB＝6cm,，P为AB上任意一点，则　 OP的取值范围是（　　）

A.5≥OP　　　　　 B.OP≤3　　　　　 C.3≤OP<5　　　　 D.3≤OP≤5

二、真空题：（每小题4分，共计40分）

13.既是中心对称又是轴对称的四边形是_____________________________.

14.三角形的两边分别为6cm、8cm,第三边是方程x²－16x＋60＝0的一个根，则此三角形的面积是____________________cm².

15.一工厂一月份的产量为25吨，第一季度的总产量为91吨，若二月、三月的平均增长率同为x%,可列方程：________________________________.

16. .最简二次根式和能合并成一项，则它们的和为_______________.

17. ⊙O上有A、B、C三点，且∠AOC=110⁰,D、B、C三点共线，则∠ABD＝_____________.

18.在同心圆中，大圆弦AB交小圆于C、D两点，大圆的半径为10cm，小圆的半径为6cm，则AC＝____________________.

19.AB为⊙O的直径，C、D为上半圆上的三等分点，E为下半圆的任意点，则∠C+∠D+∠E＝________________.　　　　　　　　　　　  D

第17题图　　　　 第18题图　　　　 第19题图　　　　 第21题图

20.已知，x=,y=，则x²-y²＝_______________.

21.AB为⊙O的直径，C、D分别位于上、下两个半圆上，且∠AOC=x⁰, ∠CDB=y⁰,则x、y间的关系式为______________________________.

22.x₁、x₂是方程x²－ax＋b＝0的两根，以x₁、x₂为边长的矩形的周长为_____________,以x₁、x₂为直角边的三角形的面积为________________.

三、解答题：（共计74分）

23.计算题：（本题12分）

已知：≈1.414, ≈1.732

　－（）^－1－2－（）⁰＋＋（－1）²（精确到0.1）

24.x为奇数，且满足＝，求.的值。（本题12分）

　

25解方程：（本题10 分）

（2x-1）＝3 x(2x-1)

26．（本题12分) 如图，△ABC的高AD、BE相交于H，AD的延长线交过△ABC三个顶点的圆于F。求证：DH＝FD

　　　　　　　　　　　　  　　　　　　　　　　

27．列方程解应用题：（本题14分）

一超市在销售中发现“佳宝”牛奶平均每天可售出20箱，每箱盈利4元，为了迎接“中秋”、“国庆”佳节，超市为了扩大销售、增加盈利，若每箱降价0.4元，则平均每天多卖8箱。

（1）要想平均每天销售这种牛奶中盈利120元，每箱牛奶应降多少元？

（2）降价多少钱时，每天就销售这种牛奶盈利额最大，最大盈利额是多少？

 

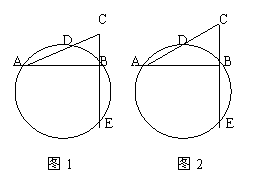
28．（本题14分）已知：在Rt△ABC中，D为AC的中点，⊙O经过A、D、B三点，CB的延长线交⊙O于E（如图1）；在满足上述条件下，当∠CAB的大小变化时，图形也随着改变（如图2）；在这个变化过程中，有些总保持着相等关系。

观察右边图形，连接图中已标明的两点，得到一条新线段，证明它与线段CE相等。