初级中学学业水平考试统一质量检测九年级数学试题
一、选择题（本题满分21分，共有7道小题，每小题3分）
1．为了解青岛市2006年初中毕业生的数学学习水平，我们随机抽取了500名九年级学生进行检测，在这个问题中下列叙述正确的是（ ）
A． 青岛市2006年全体初中毕业生是总体
B． 青岛市2006年一名初中毕业生是个体
C． 随机抽取的500名学生的数学检测成绩的方差可以反映这届学生数学成绩的优秀率
D． 随机抽取的500名学生的数学检测成绩是样本
2．⊙O1和⊙O2的半径分别是6和8，O1 O2=10，则⊙O1和⊙O2的位置关系是（ ）
A．外离 B. 外切 C. 相交 D. 内含
3. 据统计，我国近几年平均每年因土地沙漠化造成的经济损失约为547.5亿元，若一年按365天计算，用科学记数法表示我国近几年平均每天因土地沙漠化造成的经济损失约为（ ）元。
A．
B.
C.
D.
4. 如图，
ABCD的对角线交点与平面直角坐标系的原点重合，且AB∥CD∥x 轴，若点A和点B的坐标分别为
和
，则点C和点D的坐标分别是（ ）
A．
和
B. 
和
C. 
和
D.
和
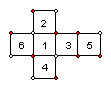
5．如图是一个均匀立方体的表面展开图，抛掷这个立方体，朝上的一面上的数字恰好等于朝下的一面上的数字的
的概率是（ ）。
A．
B. 
C.
D.
6.点A(x1,y1)和点B(x2,y2)都在双曲线
上，且当
＞
＞0时，有y1
＜y2，则函数
与（k≠0）在同一直角坐标系中的图像可能是（ ）
 | |||||
 |  | ||||
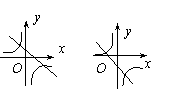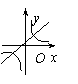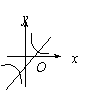A B C D
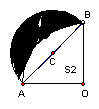7．如图，小明先作了一个圆心角为直角的扇形OAB，再以AB为直径作半圆，画出了一个如图阴影部分所示的月牙形图案，则此月牙形图案的面积S1与△AOB的面积S2之间的大小关系为（ ）
A．S1 ＜S2 B. S1 =S2 C. S1 ＞S2 D. 无法确定
二、填空题（本题满分21分，共有7道小题，每小题3分）
8. 计算：
________________
9. 小明和他的爸爸在太阳光下行走，他爸爸的身高为180cm，影长为200cm，小明比爸爸矮45cm，此刻小明的影长是 ______________ cm
10. 一个袋中有黑球10个，白球若干个，小明从袋中随机摸出10个球，记下其中黑球的个数，再把它们放回袋中，摇匀后重复上述过程20次，发现共有黑球18个，由此你能估计出袋中的白球数是 _______个。
11．如图，△ABC内接于⊙O，∠A=50°，E是
的中点，请你添加一个条件： _________,使△ABC∽△BOE。
12．如图，在直角三角形ABC中，∠C=90°，BC=1，AC=
，以B点为旋转中心将△ABC沿顺时针方向旋转至△
的位置，则A点从开始至结束所经过的路径长度为 ______________.
|
项目 | 七 | 八 | 九 | 合计 |
| 每人补助金额（元） | 91 | 90 | 80 |
|
| 人数（人） | 40 | 120 | ||
| 补助总金额（元） | 3200 | 10440 |
年级 
13. 我市某公益组织为某中学贫困家庭子女提供教材补助，右表是该中学接受补助的部分情况。请你利用所学数学知识将表格补充完整。
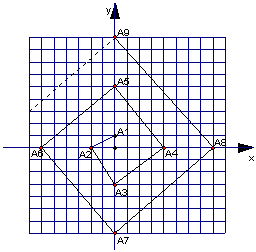14．如图，网格中最小正方形的边长为1，按图中所示的规律确定点A1、A2、A3、A4……An，若以A1、A2、A3为顶点组成三角形记为
，以A2、A3、A4为顶点组成三角形记为
……，以An、An+1、An+2为顶点组成三角形记为
（n为正整数），请你推断的面积S与n之间的关系式：
S= _________；
当S=100cm2时，n = _______.
三、作图题（本题满分6分）用圆规、直尺作图，不写作法，但要保留作图痕迹。
15．如图，小区花园内有三个亭子A、B、C，亭子间均有直线道路连接，且AB=AC。现要在道路BC上架一盏路灯D，使它到A、B两个亭子的距离相等。
（1）
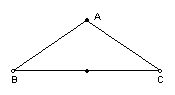在图中画出路灯D的位置；
（2） 若DC=8米，DA=4米，求亭子B、C间的距离。
四、解答题（本题满分72分，共有9道小题）
16．（本小题满分6分）
化简：
17．（本小题满分6分）
饮食公司为某学校提供5元（A）、3元（B）和4元（C）三种价格的午餐供师生选择（每人限订一份），图①是5月份的销售情况统计图，这个月一共销售了10000份午餐。
（1） 写出师生购买午餐费用的中位数和众数。
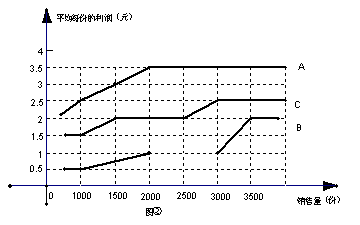
（2） 如果5月份三种午餐的销售量与其平均每份的利润间的关系大致如图②所示，求该公司这个月在这所学校销售午餐共盈利多少元？
 |
18、（本小题满分6分）
某酒店为了吸引顾客，制做了一个可以自由转动的转盘，转盘等分成16份（如图），并规定：顾客每次消费200元以上（不包括200元），就能获得一次转动转盘的机会，如果转盘停止后，指针正好对准八折、七折、五折区域，顾客就可以获得此项打折优惠。
（1） 如果一名顾客消费了300元，他获得打折优惠的概率是多少？
（2） 参加这个活动的顾客每转动一次转盘，平均可享受几折优惠？
19、（本小题满分6分）
如图，公路AB边有一人工湖，湖面上原有一座桥CD与公路垂直相通，因桥面有一部分断裂，为测桥长，站在完好的桥头D处测得路边的小树B在D的北偏西37.4°,前进50米到达E处，又测得小树B在E的北偏西45°。
（参考数据：
；
；
）
（1）
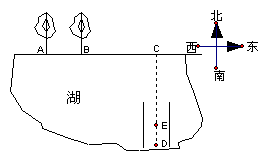计算桥CD的原有长度；
（2） 若路边小树A与小树B相距50米，则小树A在点D的什么方向？
20、（本小题满分8分）
| 大蒜品种 | 甲 | 乙 | 丙 |
| 每辆汽车的满载量（吨） | 8 | 10 | 11 |
| 运输每吨大蒜获利（元） | 220 | 210 | 200 |
某运输公司计划用10辆汽车将甲、乙、丙三种大蒜共100吨运到外地，每辆汽车只能装同一种大蒜，且必须满载，每种大蒜不少于一车。
（1） 设用x辆车装甲种大蒜，y辆车装乙种大蒜，根据右表信息写出y与x之间的函数关系式，并说明有哪几种符合要求的运输方案。
（2）设此次运输的利润为P，求P与x之间的函数关系式，并说明按哪种方案运输利润最大。
21、（本小题满分8分）
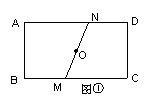如图①，在矩形ABCD中，AD＞AB，O为对角形的交点，过O作一直线MN分别交BC、AD于M、N。
（1） 求证：梯形ABMN的面积等于梯形CDNM的面积；
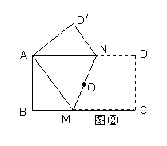
（2） 如图②，将矩形ABCD以MN为轴对折，当MN满足什么条件时，对折后能使C点恰好与A点重合？（只写出需要满足的条件即可，不要求证明）
（3） 在（2）的条件下，判断四边形AMCN是什么特殊四边形？写出证明过程。
22、（本小题满分10分）
某广告公司设计一幅周长为12米的矩形广告牌，广告设计费为每平方米100元。设矩形的一边长为x米，面积为S平方米。
（1） 求出S与x之间的函数关系式；
（2） 当x为多少米时，广告设计费最高？求出这个费用；
（3） 当x为多少米时，广告公司能获得500元的设计费？
（4） 当x的取值在什么范围内时，可使获得的广告设计费不低于500元？
23、（本小题满分10分）
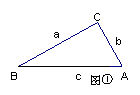
在△ABC中，∠A、∠B、∠C所对的边分别用a、b、c表示。
（1） 如图①，在△ABC中，∠A=2∠B，且∠A=60°。
求证：
。
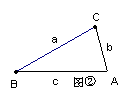
（2）
如果一个三角形的一个内角等于另一个内角的2倍，我们就称这样的三角形为“倍角三角形”。本题图①中的三角形是特殊的倍角三角形，那么对于任意的倍角三角形（如图②），当∠A=2∠B时，关系式是否仍然成立？若成立，证明你的结论；若不成立，举出反例。
（3） 是否存在这样的倍角三角形，其三边长恰为三个连续的正整数？若存在，求出其三边长；若不存在，说明理由。
24、（本小题满分12分）
如图①，边长分别为
和3的两个等边三角形纸片ABC和
C′D′E′叠放在一起（C与C′重合）。
（1）
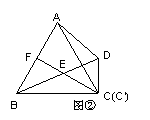操作：固定△ABC，将△C′D′E′绕点C顺时针旋转30°得到△CDE，连接AD、BE，CE的延长线交AB于F（如图②）；
探究：在图②中，线段BE与AD之间有怎样的大小关系？证明你的结论。
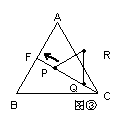（2）
操作：如图②中的△C′DE沿着CF方向以每秒1个单位的速度平移，平移后的△C′DE设为△PQR（如图③）；
探究：设△PQR移动的时间为x 秒，△PQR与△AFC重叠部分的面积为y,求y与x之间的函数解析式，并写出自变量x的取值范围。
（3） 操作：将图①中的△C′D′E′固定，将△ABC移动，使顶点C落在C′E′的中点，边BC交D′E′于点M，边AC交D′C′于点N，设∠AC C′=α（ 30°＜α＜90° ）（如图④）；
探究：在图④中，线段C′E×E′M的值是否随α的变化而变化？如果没有变化，求出C′E×E′M的值；如果有变化，说明理由。
| ||||||
|
| |||||