初三（上）第一次月考数学试题

初三（上）第一次月考数学试题

（120分钟）

班级__________姓名____________

得分	评卷人

一、选择题：（本大题10个小题，每小题4分，共40分 ）在每个小题的下面，都给出了代号为A、B、C、D 的四个答案，其中只有一个是正确的，请将正确答案的代号填在题后的括号中．

1、化简的结果是――――――――――――――――――――――――――――（　　）

　　A．－2　　　　B．±2　　　　 C．2　　　 D．4

2、已知x=1是一元二次方程x²-2mx+1=0的一个解，则m的值是 ――――――――――― (　　)

A．1　　　　　　　　　　　 B．0

C．0或1　　　　　　　　　 D．0或-1

3、计算的结果是―――――――――――――――――――――――――――（　　）　　　　　　　　　　　　　　　　　　　

　A、3　　 　　　 B、　　 　　　　 C、2　　　 　　　D、

4、随着新农村建设的进一步加快，湖州市农村居民人均纯收入增长迅速。据统计，2005年本市农村居民人均纯收入比上一年增长14.2%。若2004年湖州市农村居民人均纯收入为a元，则2005年本市农村居民人均纯收入可表示为――――――――――――――――――――――――――――――（　　）

　 A、14.2a元　　 B、1.42a元　　　C、1.142a元　　　D、0.142a元

5、下列图形中，是中心对称图形的是-――――――――――――――――――――――－（　　）

　A.菱形　　　　B.等腰梯形　　　 C.等边三角形　　D.等腰直角三角形

6、一元二次方程的两个根分别为―――――――――――――――――――(　　)

　　(A)x_l=1，x₂=3　　　　(B)x_l=1，x₂=-3　　

　　(C)x₁=-1，x₂=3　　　(D)x_I=-1，x₂=-3　

7、 关于x的一元二次方程kx²+2x－1=0有两个不相等的实数根, 则k的取值范围是――――（　　 ）

A. k>－1　　　　　B. k>1　　　　　　C. k≠0　　　　　 D. k>－1且k≠0

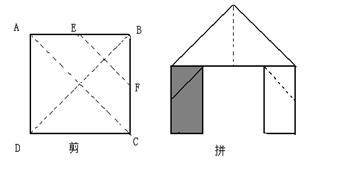
8、如图，正方形硬纸片ABCD的边长是4，

点E、F分别是AB、BC的中点，若沿左图

中的虚线剪开，拼成如下右图的一座“小

别墅”，则图中阴影部分的面积是―――――――――――――――――――――――――（　　　 ）。

A．2　　 B．4　  C．8　  D．10

9、某种手机卡的市话费上次已按原收费标准降低了m元/分钟,现在两次下调20％，使收费标准为n元/分钟,那么原收费标准为 ――――――――――――――――――――――――――（　　 ）

　 A、( – m )元/分钟　　　　　　  B、(　 + m )元/分钟

　 C、(   – m )元/分钟　　　　　　  D、( + m )元/分钟

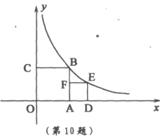10．如图，正方形OABC，ADEF的顶点A，D，C在坐标轴上，点F在AB上，点B，E在函数 的图象上，则点E的坐标是

A．

B．

C．

D．

得分	评分人

二．填空题：（本大题10个小题，每小题3分，共30分）在每小题中，请将答案直接填在题后的横线上．

11、代数式在实数范围内有意义，则x的取值范围为________________．

12、写出一个有实数根的一元二次方程：　　　　　　　　　　　　 。

13、方程x（x＋3）＝x＋3的解是　　　　　　　　　　　 

14、 如果最简二次根式与可以合并成一个二次根式, 则a=__________.

15、 已知2<x<5, 化简 =___________.

16、已知等腰三角形ABC中，BC=8,AC、AB两边长分别是关于x的方程x²－10x＋m＝0的两根，则m的值是____________。

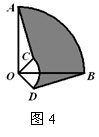
17、如图4，圆心角都是90°的扇形OAB与扇形OCD叠放在一起，

OA＝3，OC＝1，分别连结AC、BD，则图中阴影部分的面积为__________。

18、小王利用计算机设计了一个计算程序，输入和输出的数据如下表：

输入	…	1	2	3	4	5	…
输出	…						…

那么，当输入数据为8时，输出的数据为　　　　　　．

19、若x、y为实数，且y=，则的值是_________．

20、已知（x+y）（x+y+2）-8=0，求x+y的值，若设x+y=z，则原方程可变为_______，所以求出z的值即为x+y的值，所以x+y的值为______．

得分	评卷人

三．解答题：（本大题8个小题，共80分）下列各题解答时必须给出必要的演算过程或推理步骤．

21、计算。（每小题5分）

（1）（+）+（-）　　　 (2) ．计算：

22、解下列方程：（每题4分，共16分）

（1） （x-1）²= 9　　　　　　　　　　　　　　  (2 )　 x ²－x＋2＝0

（3）　3 x ²－x－2＝0　　　　　　　　　　　  （4）　（x－6）² -（3－2x）²=0

23、（8分）已知关于x的方程的一个解与方程的解相同．

⑴求k的值；

⑵求方程的另一个解.

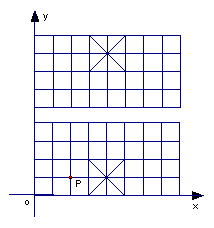
24、如图，我们给中国象棋棋盘建立一个平面直角坐标系

（每个小正方形的边长均为1），根据象棋中“马”走“日”

的规定，若“马”的位置在图中的点P．

⑴ 写出下一步“马”可能到达的点的坐标　　　　　　　　

　　　　　　　　 ；

⑵ 顺次连接⑴中的所有点，得到的图形是　　　　　　

图形（填“中心对称”、“旋转对称”、“轴对称”）；

⑶ 指出⑴中关于点P成中心对称的点　　　　　　　．

25、（本题8分）如图是规格为8×8的正方形网格,请在所给网格中按下列要求操作：

⑴ 请在网格中建立平面直角坐标系, 使A点坐标为(－2，4)，B点坐标为(－４，2)；

⑵ 在第二象限内的格点上画一点C, 使点C与线段AB组成一个以AB为底的等腰三角形, 且腰长是无理数, 则C点坐标是　 　　 ， △ABC的周长是　　　　　　 (结果保留根号)；

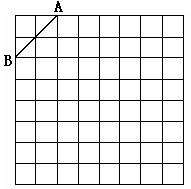⑶ 画出△ABC以点C为旋转中心、旋转180°后的△A′B′C, 连结AB′和A′B, 试说出四边形ABA′B′是何特殊四边形, 并说明理由.

26、某商场将每件进价为80元的某种商品原来按每件100元出售，一天可售出100件．后来经过市场调查，发现这种商品单价每降低1元，其销量可增加10件．

（1）求商场经营该商品原来一天可获利润多少元？

（2）若商场经营该商品一天要获利润2160元，则每件商品应降价多少元？

27、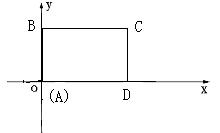（10分）如图所示，在直角坐标系中，矩形ABCD的边AD在x轴上，点A在原点，AB＝3，AD＝5．若矩形以每秒2个单位长度沿x轴正方向作匀速运动．同时点P从A点出发以每秒1个单位长度沿A－B－C－D的路线作匀速运动．当P点运动到D点时停止运动，矩形ABCD也随之停止运动．

（1）求P点从A点运动到D点所需的时间；

（2）设P点运动时间为t（秒）。

①当t＝5时，求出点P的坐标；

②若⊿OAP的面积为s，试求出s与t之间的函数关系式（并写出相应的自变量t的取值范围）．

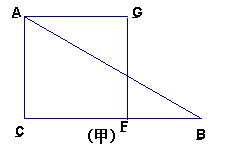
28、(本题满分10分)如图,把正方形ACFG与Rt△ACB按如图(甲)所示重叠在一起,其中AC=2, ∠BAC=60⁰,若把Rt△ACB绕直角顶点C按顺时针方向旋转,使斜边AB恰好经过正方形ACFG的顶点F,得△A′B′C′，A B分别与A′C,

A′B′相交于D、E,如图(乙)所示.

①. △ACB至少旋转多少度才能得到△A′B′C′?说明理由.

②.求△ACB与△A′B′C′的重叠部分(即四边形CDEF)的面积(若取近似值,则精确到0.1)