初三毕业班第二次调研考试数学试卷
| 题号 | 一 | 二 | 三 | 四 | 总分 | ||||||
| 1-10 | 11-18 | 19-23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | ||
| 得分 | |||||||||||
第一部分（选择题，共 30 分）
注意事项：
答卷前将密封线内的项目填写清楚
一、选择题：（本大题共10小题，每小题3分，共30分.在每小题给出的4个选项中，只有1项是符合题目要求的，请正确答案的序号填写在下面的括号内）.
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
1．4的平方根是
A ．-2 B．2 C．±2 D．±4
2．生物学家发现某种病毒的长度约为0.000043mm，则该长度用科学记数法表示正确的是
A．4.3×10－5mm B．4.3×10-6mm C．43×10－4mm D．0.043×10－6mm
3．在数学活动课上，老师和同学们判断一个四边形门框是否为矩形，下面是某学习小组的4位同学拟定的方案，其中正确的是
A．测量对角线是否相互平分 B．测量两组对边是否分别相等
C．测量一组对角是否都为直角 D．测量其中三角是否都为直角
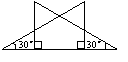
4．将两个全等的有一个角为30°的直角三角形拼成右图形状，其中
两条较长的直角边在同一条直线上，则图中等腰三角形的个数是
A．1 B．2 C．3 D． 4
5．下列说法：①x2-xy+y-2是二次三项式；②
是最简分式；③
与
是同类二次根式；④ 
是最简二次根式，其中正确的个数有
A．1个 B． 2个 C．3个 D．4个
6.．某实验中学初三年级进行了一次数学测试，参加考试的有859人，为了解这次数学测试的大致情况，下列所抽取的样本中比较合理的是
A．抽取前250名同学的数学成绩 B．抽取后250名同学的数学成绩
C．抽取中间250名同学的数学成绩 D．抽取学号是3的倍数的同学的数学成绩
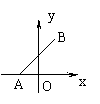
7．如右图所示，已知点A（-1，0）和点B（1，2），在坐标轴上确定点P，
使得ΔABP为直角三角形，则满足这样条件的点P共有
A．7个 B．6个 C．4个 D．3个
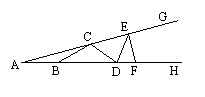8．如图，C、E和B、D、F分别在∠GAH的两边上，且
AB=BC=CD=DE=EF，若∠A=18°，则∠GEF的度数是
A．80° B．90° C．100° D．108°
9．二次函数
(a≠0)的图象一定不同时经过P、Q两点，则P、Q两点的坐标可以是
Ａ．P（-1，4），Q（3，4） Ｂ．P（-1，4），Q（-1，6）
Ｃ．P（-1，3），Q（4，4） Ｄ．P（4，4），Q（3，-1）
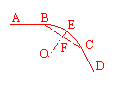
10．如图，是一段公路弯道的示意图，该弯道是由直线AB、CD与圆弧
BEC相切连接而成，E为弧BC的中点，O为圆弧的圆心，OE交BC于点F，若弦BC＝600m，EF＝100m，则该弯道的半径为
A．400m B．500m C．600m D．700m
第二部分（非选择题，共 120 分）
注意事项：第二部分试题答案用钢笔或圆珠笔直接写在试卷上。
| 得 分 | 评卷人 | 复核人 |
二、填空题(本大题共8小题，每小题3分，共24分).
11．写出一个图象分布在第二、四象限的反比例函数解析式： ；
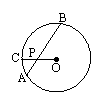
12．已知⊙O的半径OC被弦AB平分于点P，若AP=3，PB=9，则OC= ；
13．二次函数y=2x2+x-5的顶点坐标是 ；
14．如图，在三角形纸片ABC中，∠C＝90°，∠A＝30°，AC＝3，折叠
该纸片，使点A与点B重合，折痕与AB、AC分别相交于点D和点E，折痕
DE的长为 ；
15．要给一边长为a米的正方形桌面上铺上正方形的桌布，桌布的四周均超出桌面0.1米，则桌布的面积为 米2；
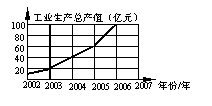
16．如图是根据某市2002年至2006年（年初）工业生产总值绘制
的折线统计图，从统计图可以看出：增长幅度最大的是 年；
17．一个圆锥的底面直径是20cm，母线长为30cm，则该圆锥的
侧面积为 cm2；
18．已知关于x的方程x2-mx+2m2-7=0的两个实数根的积为1，则这两个实数根的和为 ；
| 得 分 | 评卷人 | 复核人 |
三、解答题：（本大题共5小题，计36分）
19.（本题满分10分）
（1）计算： 
；
（2）化简：
÷
20．（本题满分6分）
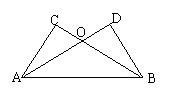
如图所示，已知AC＝BD，AD与BC相交于点O．请添加一个条件，使△AOC≌△BOD，并根据你添加的条件，证明你的结论．
 |
21．（本题满分6分）
为庆祝"六一"儿童节，某市中小学统一组织文艺汇演．甲、乙两所学校共92人参加演出，其中甲校人数多于乙校人数，且甲校人数少于90人，现准备统一购买演出服装，下面是某服装厂给出的演出服装的价格表：
| 购买服装的套数 | 1套至45套 | 46套至90套 | 91套及以上 |
| 每套服装的价格 | 55元 | 50元 | 45元 |
如果两所学校分别单独购买服装，一共应付4800元．
(1)甲、乙两所学校各有多少学生准备参加演出？
(2)如果甲校有10名同学抽调去参加书法绘画比赛不能参加演出，请你为两所学校设计一种最省钱的购买服装方案．
22．（本题满分7分）
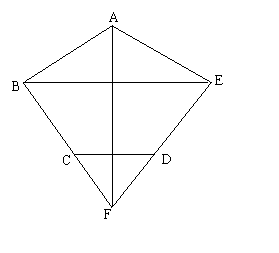
已知：在五边形ABCDE中，AB＝AE，BC＝DE，∠BAE＝∠BCD＝∠CDE＝120°，BC、ED的延长线相交于点F．
（1）求证：四边形BCDE是等腰梯形；
（2）连接AF，求证：AF垂直平分BC．
 |
23．（本题满分7分）
解方程：(x2+x)2－x2－x－2＝0
| 得 分 | 评卷人 | 复核人 |
四、解答题：（本大题共7小题，计60分）
24．（本题满分6分）
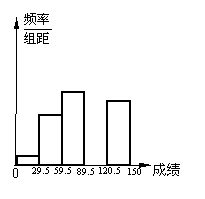在第一次调研考试结束后，我们从全市6000应届初三学生中抽取了一部分学生的成绩作为样本进行数据处理，得到如下的频率分布表和频率分布直方图（学生的成绩均是正整数）．
| 分组 | 频数 | 频率 |
| 0－29.5 | 10 | 0.02 |
| 29.5－59.5 | 80 | 0.16 |
| 59.5－89.5 | 110 | 0.22 |
| 89.5－120.5 | ||
| 129.5－150 | 100 | 0.2 |
| 合计 | 1 |
（1）根据上述数据，补全频率分布表和频率分布直方图；
（2）若成绩在90以上（含90分）属合格成绩，请你估计一下，全市大约有多少人取得了合格成绩？
25．（本题满分8分）
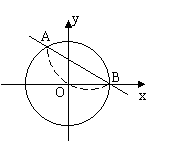
如图所示，半径为2的圆的圆心在平面直角坐标系的原点，与x轴正向相交于点B，将圆沿直线AB对折，直线AB上方的圆弧经过折叠后正好通过坐标原点O．
（1）求A点坐标；
（2）求直线AB的解析式．
 |
26．（本题满分8分）
数学兴趣小组在一次活动中，设计了下表：
| n | 2 | 3 | 4 | 5 | … |
| a | 22-1 | 32-1 | 42-1 | 52-1 | … |
| b | 4 | 6 | 8 | 10 | … |
| c | 22+1 | 32+1 | 42+1 | 52+1 | … |
(1)请你观察表中a、b、c与n之间的关系，并用含自然数n(n>1)的代数式表示为：a= ，
b= ，c= ；
(2)猜想：以a、b、c为边的三角形是否为直角三角形？并证明你的结论．
ｈ
27．（本题满分8分）
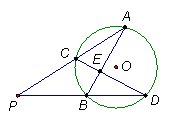
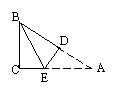
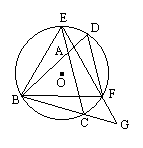
如图所示，△ABC是等边三角形，⊙O过点B、C，且与BA、CA的延长线相交于点D、E，弦DF∥AC，EF的延长线交BC的延长线于点G，且有CG∶BC＝1∶2．
（1）△BEF也是等边三角形吗？请说明理由；
（2）若△ABC的边长是4，求△BEF的边长．
28．（本题满分8分）
我们知道：只有一个未知数，并且未知数的最高次数为2的方程叫做一元二次方程，类似地，我们把只有一个未知数，并且未知数的最高次数为2的不等式叫做一元二次不等式，例如：x2-2x-3<0就是一个一元二次不等式．下面我们讨论如何解这个一元二次不等式：
解：将原不等式的左边因式分解得到：(x-3)(x+1)<0……①
∵(x-3)、(x+1)既可以分别代表一个代数式，又可以分别代表一个实数，
∴由
可知不等式①可化为：
②或
③；
不等式组②无解，不等式组③的解集为：-1<x<3，故原不等式的解集为：-1<x<3．
（1）阅读并理解上述内容，并在上面的空格处填上恰当的道理；
（2）请你运用类比的方法，仿照上面的过程，解不等式：
≤0．
29．（本题满分10分）
已知二次函数y=ax2+bx+c(a=1)的图象与x轴有两个不同的交点A和B，A、B两点的横坐标分别为x1、x2，x1、x2是关于x的一元二次方程x2+2(m-2)x+m2-3m+3＝0的两个根，且x1＜x2，m≥-1．
(1)若x12+x22=6，求m的值；
(2)若代数式
的值为4，求相应的二次函数的解析式；．
（3）对于(2)中所求的二次函数，当自变量x分别取2006和2007时，得到相应的函数值，不妨记为y1和y2，试确定y1和y2的大小关系
30．（本题满分12分）
如图所示，在梯形铁皮ABCD中，∠DAB＝∠ABC＝90°，AD＜BC，AD＝m，AB＝n，BC=p，且关于x的方程：mx2+nx+p=0有两个相等的实数根．
（1）求证：AD+BC＝CD；
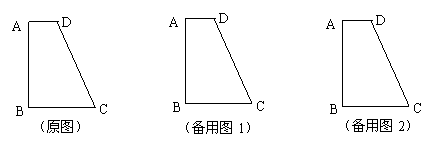（2）现要在该梯形铁皮上剪下一块面积最大的半圆形铁皮，圆心在其中的一条边上，你认为应该如何下料，并说明你的理由．