初三第一次月考数学科试卷
本试卷共7页 共28题 满分：120分 考试时间：120分钟
一、填空（每题3分，共30分）
1、方程
的解为
。
2、点P(-3,2)关于原点O对称的点P1的坐标为 。
3、已知x=1是方程
的一个解，则m＝
。
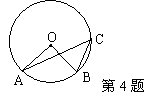
4、如图，点A、B、C三点在⊙O上，且
，
则
。
5、填写：
＝(x+ )2
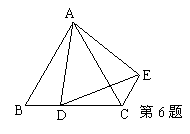6、如图，等边△ABC的边BC上一点D，△ABD绕
点A旋转到△ACE，则∠DAE＝ °
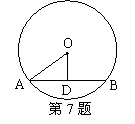
7、如图，线段AB为⊙O的一条弦，OD⊥AB于D，
且OD=8cm，AB＝12cm，则该圆的半径为 。
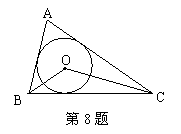
8、如图所示，⊙O为△ABC的内切圆，
，
，则
°
9、一个直角三角形的两条直角边长是方程
的两个根，则此直角三角形外接圆的半径等于
。
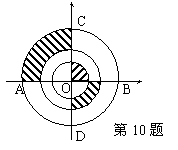
10、如图所示，三圆同心于O，AB=4cm，CD⊥AB于O，则图中阴影部分的面积为
。
二、选择题（每题3分，共30分）
11、下列几何图形中，是中心对称图形而不是轴对称图形的是（ ）
A、线段 B、圆 C、矩形 D、平行四边形
12、一元二次方程
的根的情况是（ ）
A、有两个不相等的实数根 B、有两个相等的实数根
C、没有实数根 D、无法判断
13、如图所示的几幅图中，可以旋转180°与自身重合的是（ ）
 |
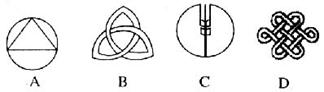14、⊙O1与⊙O2的半径分别为4cm和5cm，若O1O2＝10cm，则两圆的位置关系是（ ）
A、外离 B、外切 C、相交 D、内切
15、方程
的解为（ ）
A、
B、
，
C、
D、
16、一正多边形的一个外角为90°，则它的边心距与半径之比为（ ）
A、1:2 B、
C、
D、1:3
17、下列说法正确的是（ ）
A、与圆有公共点的直线是圆的切线 B、过三点一定能作一个圆
C、垂直于弦的直径一定平分这条弦 D、三角形的外心到三边的距离相等
18、某商场三月份的利润是82.75万元，一月份的利润是25万元，若利润平均每月增长率为x，则依题意列方程为（ ）
A、
B、
C、
D、
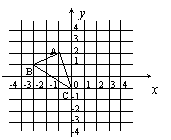19、如图，若将△ABC的绕点C顺时针旋转90°后得到
，则A点的对应点
的坐标是（ ）
A、(－3,－2)
B、(2,2)
C、(3,0)
D、(2,1)
20、若
、
是方程
的两个根，则：
的值为（ ）
A、2005 B、2003 C、－2005 D、2007
初三第一次月考数学科试卷答 题 卷
一、填空（每题3分，共30分）
1、 2、 3、 4、
5、 6、 7、
8、 9、 10、
二、选择题（每题3分，共30分）
| 题次 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 答案 |
三、解答题（第21、22、23、24题每题6分，第25、26题每题8分，共40分）
21、解下列一元二次方程（6分）
（1）
（2）
 |
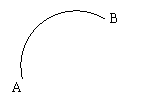22、已知弧AB，请用尺规作出弧AB所在圆的圆心（6分）
（不写作图步骤，但保留作图痕迹）。
23、点A、B、D、E在⊙O上，弦AE与弦BD的延长线相交于点C，给出下列三个条件。（6分）
①AB是圆的直径 ②D是BC的中点 ③AB=AC
请在上述三个条件中选取两个作为已知条件，第三个作为结论，写出一个你认为正确的命题，并加以证明。
条件：已知：
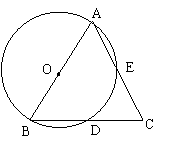结论：求证：
证明：
24、△ABC中，∠B＝10°，∠ACB＝20°，AB=4cm，△ABC逆时针旋转一定角度后与△ADE重合，且点C恰好成为AD中点。（6分）
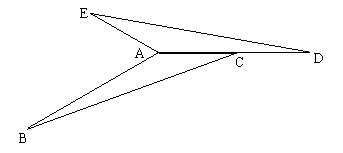（1）指出旋转中心，并求出旋转度数。
（2）求出∠BAE的度数和AE的长。
26、应用题（8分）
在一幅长80cm，宽50cm的矩形风景画的四周各镶一条宽度相等的金色纸边，制成一幅矩形挂图，如图所示，要使制成后的挂图的面积是5400cm2，求金色纸边的宽。
 |
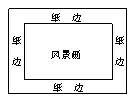四、计算与证明（10分）
27、如图，已知AB是⊙O的直径，⊙O过BC的中点D，且ED是⊙O的切线。
（1）求证：DE⊥AC
|
 |
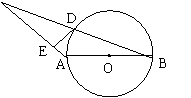五、综合题（10分）
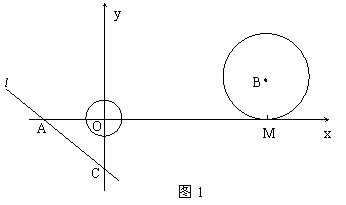
28、如图1，在平面直角坐标系中，以坐标原点O为圆心的⊙O的半径为
，直线
与坐标轴分别交于A、C两点，点B的坐标为(4,1)，⊙B与x轴相切于点M。
（1）求点A的坐标及∠CAO的度数；
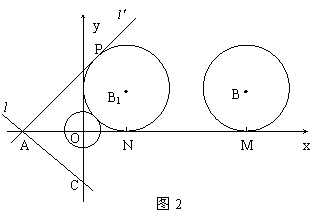
（2）⊙B以每秒1个单位长度的速度沿x轴负方向平移，同时，若直线
绕点A顺时针匀速旋转，当⊙B第一次与⊙O相切时，直线也恰好与⊙B第一次相切，见图（2）求B1的坐标以及直线AC绕点A每秒旋转多少度？
（3）若直线不动，⊙B沿x轴负方向平移过程中，能否与⊙O与直线同时相切。若相切，说明理由。
 |
2007届初三第一次月考数学科试卷
答 案
一、填空（每题3分，共30分）
1、 3或-3 2、 （3，-2） 3、 2 4、 40°
5、 9 3 6、 60° 7、 10
8、 122° 9、 2.5 10、 ∏
二、选择题（每题3分，共30分）
| 题次 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 答案 | D | C | D | A | B | B | C | D | C | B |
21、解下列一元二次方程（6分）
⑴ 
，
⑵ 
22．略
23．略
24．① A为旋转中心，旋转角为150°
② ∠BAE=60°，AE的长为2
25．①BC的长为
； ②AD=BD=
26．金色纸边的宽为5㎝，
27．（1） 证明OD为△ABC的中位线，得出OD∥AC，从而得DE⊥AC
（2）⊙O的半径为
。
| |
，∠CAO=45°；
（2）B1的坐标（
以及直线AC绕点A每秒旋转30度
（3） 能，设⊙B与⊙O第二次相切时⊙B的圆心为B2，作B2E⊥AC于E，
作OH⊥AC于H，则四边形B2EHO为平行四边形，则B2E=OH=1，故此时⊙B与直线同时相切。