初三第一学期期中练习卷

初三第一学期期中练习卷姓名　　　　

一、细心填一填（每空２分，共３６分）：

１、的相反数是　　　　　，的绝对值是　　　　　　，２的平方根是　　　　　　　。

２、随着中国综合国力的提升，近年来全球学习汉语的人数不断增加．据报道，2005年海外学习汉语的学生人数已达38 200 000人，用科学记数法表示为　　　　  　　人.

３、函数中，自变量x的取值范围为　　　　 ；当ｘ＝　　　　时，分式没有意义。

４、方程的解是　　　　　　　　　；方程的解是　　　　　　　。

５、已知，则的值等于　　　　  .

6、已知３是方程ｘ^２＋５ｘ－３ｍ＝０的一个根，则另一个根是　　　　　，ｍ＝　　　　　　。

7、已知圆锥的底面半径为3cm，母线长为4cm，则该圆锥的侧面展开图的面积为　　 　　　　cm²。

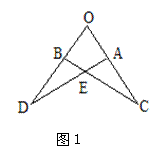
8、如图1，若△OAD≌△OBC，且∠0=65°，∠C=20°，则∠OAD=　　　　。

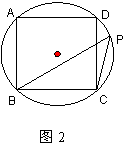
9、如图2，正方形ABCD的顶点都在⊙O上，P是弧DC上的一点，则∠BPC的度数是_________。

	图１

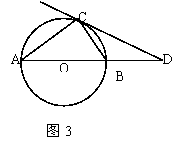
10、已知：如图3，AB是⊙O的直径，BD=OB，∠CAB＝30°，请根据已知条件和所给出的图形，任意写出两个正确的结论（除OA=OB=BD外）：（１）　　　　　　　　　；（２）　　　　　　　　　　。

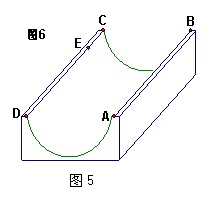11、如图5，这是一个供滑板爱好者使用的U型池，该U型池

可以看作是一个长方体去掉一个“半圆柱”而成，中间可供滑

行部分的截面是半径为的半圆，其边缘AB = CD =，

点E在CD上，CE =，一滑板爱好者从A点滑到E点，则

他滑行的最短距离约为　　　　　  。（边缘部分的厚度忽略

不计，结果保留整数）

12、如图，在直线m上摆故着三个正三角形:△ABC、△HFG、△DCE,

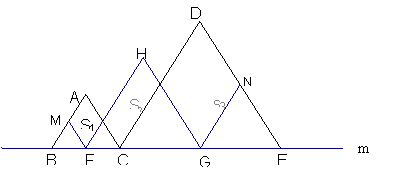已知BC=CE,F、G分别是BC、CE的中点，FM∥AC，GN∥DC．设图中

三个平行四边形的面积依次是S₁,S₂,S₃,若S₁+S₃=10，则S₂=　　　 。

 

二、精心选一选（每小题３分，共１８分）：

13、下列运算正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　  (　 　 )

　(A)=±2　  (B)2^-3=-6　　(C)x²·x³=x⁶　　(D)(-2x)⁴=16x⁴

14、关于ｘ的方程无解，则ｍ的值为　　　　　　　　　　　　　　　　（　　　）

（A）-1　　　　（B）0　　　　 （C）1　　　　　  （D）2

15、关于x的方程4x²+6x+k=0有两个实数根，那么k的取值范围是　　　　　  （　　　）

　 A、k≤　　  B、k≥　　　 C、k＜　　　　D、k＞

16、钟表的轴心到分针针端的长为5cm，那么经过40分钟，分针针端转过的弧长是　　　　(　 　　)

　 (A)　　 (B) 　 (C) 　　(D)

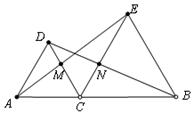
17、方程的如图，△DAC和△EBC均是等边三角形，AE、BD分别与CD、CE交于点M、N，有如下结论：①△ACE≌△DCB； ②CM＝CN；③AC＝DN。其中，正确结论的个数是 (　　　)

(A) 3个　　　　　　　　　  （B）2个

 (C) 1个　　　　　　　　　  （D）0个　

18、已知⊙O的半径OA=2，弦AB、AC的长分别是、，则∠BAC的度数为　　　　（　　　）

A.15°　　　B.75°　　　　  C.15°或75°　　　　　 D.15°或45°

三、简答题：
19、（每题４分）计算：（１）　　（２）

20、（每题４分）解方程：（１）　　　　（２）　　　（３）

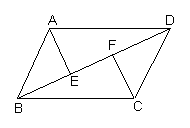
21、（满分５分）如图8，ABCD中，AE⊥BD于E，CF⊥BD于F。

求证：AE = CF

22、（满分６分）已知关于ｘ的一元二次方程，（１）若方程有两个相等的实数根，求ｍ的值；（２）若方程的两实数根之和等于ｍ^２－９ｍ＋２，求的值。

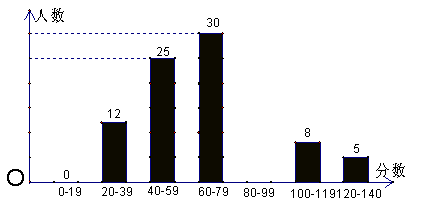23、（满分4分）阳光中学举行应用数学知识竞赛。已知竞赛成绩都是整数，试题满分为140分，现从参赛学生中随机抽取100名学生的成绩进行统计分析，得到如下图：（1）将统计图补充完整；（2）竞赛成绩的中位数落在　　　　分数段内；

（3）若共有500名学生参加本次竞赛，请你用样本估计总体的统计思想，

写出一条信息　　　　　　 　　　

　　　　　　　　　　　　　　　。

24、（满分6分）在Rt△ABC中，∠C=90°，AC=3，BC=4。（1）求AB的长；（2）如图，已知P为BC的中点，以P为圆心的⊙P与AB相切于点D。若以C为圆心的⊙C与⊙P相切，求⊙C的半径。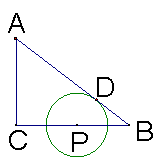

25、（满分７分）两条平行直线上各有个点，用这对点按如下的规则连接线段；

①平行线之间的点在连线段时，可以有共同的端点，但不能有其它交点；

②符合①要求的线段必须全部画出；

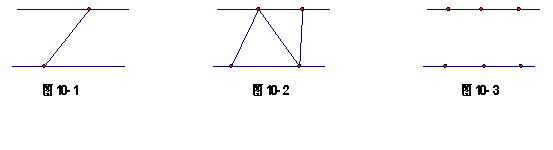
图10-1展示了当时的情况，此时图中三角形的个数为0；

图10-2展示了当时的一种情况，此时图中三角形的个数为2；

（1）当时，请在图10-3中画出使三角形个数最少的图形，此时图中三角形的个数为

　　　　 个；（４分）

（2）试猜想当对点时，按上述规则画出的图形中，最少有多少个三角形？（２分）

（3）当时，按上述规则画出的图形中，最少有多少个三角形？（１分）

26、（满分8分）某商场将每件进价为80元的某种商品原来按每件100元出售，一天可售出100件．后来经过市场调查，发现这种商品单价每降低1元，其销量可增加10件．

（1）求商场经营该商品原来一天可获利润多少元？

（2）设后来该商品每件降价x元，，商场一天可获利润y元．

①若商场经营该商品一天要获利润2160元，则每件商品应降价多少元？

②求出y与x之间的函数关系式；并求出降价多少元时，所获得的利润最大？最大利润是多少？

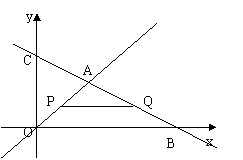
27、（满分10分）如图：在平面直角坐标系中，两个函数，的图像交于点A。动点P从点O开始沿OA方向以每秒１个单位的速度运动，做PQ∥ｘ轴交直线BC于点Q，以PQ为一边向下作正方形PQMN，设它与△OAB重叠部分的面积为S。

（１）求点A的坐标；

（２）试求出点P在线段OA上运动时，S与运动时间ｔ（秒）的关系式；

（３）在（２）的条件下，S是否有最大值？若有，求出ｔ为何值时，S有最大值，并求出最大值；若没有，请说明理由；

（４）若点P经过点A后继续按原方向、原速度运动，当正方形PQMN与△OAB重叠部分面积最大时，运动时间ｔ满足的条件是　　　　　　　　　。

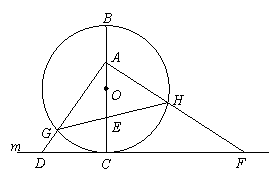28、（满分10分）如图，⊙O的直径BC=4，过点C作⊙O的切线m，D是直线m上一点，且DC=2，A是线段BO上一动点，连接AD交⊙O于点G，过点A作AD的垂线交直线M于点F，交⊙O于点H。连接GH交BC于点E。

（1）当A是BO的中点时，求AF的长；

（2）若∠AGH=∠AFD，求△AGH的面积。