初三调研考试数学试卷
一、填空题：(每空2分，共38分)
1.
的相反数是___________， 的绝对值是
。
的算术平方根是___________。
2. 点（2，3）关于X轴对称点的坐标为_____________。
3. 台湾是我国最大的岛屿，总面积 为 35989.76平方千米，这个数据可用科学记数法表示为 _____________平方千米（保留两个有效数字）。
4.
设X1,X2
是方程x2-2x-1=0 的两实数根 ，则x1+x2=____________,x1x2＝___________。
5. 写出－ab2 的一个同类项___________。
6. 函数y=
中，自变量x的取值范围是______________;
函数y=
中自变量x的取值范围是
______________。
7. 若函数y=
的图象经过点（1，-2），则k的值是______________。
8. 某校初三（1）班全体同学在“支援灾区献爱心”活动中都捐了款，具体捐款情况如下表，则该班学生捐款的平均数是__________元，中位数是________元 。
| 捐款数（元） | 1 | 2 | 3 | 4 |
| 捐款人数 | 2 | 24 | 21 | 3 |
9. 等腰△ABC中AB=AC,∠BAC=120°,.则cosB=___________。
10. 分解因式：x2-4y2=___________________。
11. 已知圆锥的母线长是5cm，底面半径是 3cm ，则这个圆锥的侧面积是 ______________cm2 。
12.
已知梯形的中位线长为5cm,高为4cm,则此梯形的面积为________cm2。
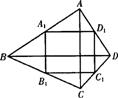
13. 如图，四边形ABCD的两条对角线AC、BD互相垂直，A1B1C1D1是四边形ABCD的中点四边形．如果AC=8，BD=10，那么四边形A1B1C1D1的面积为
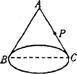14．如图，有一圆锥形粮堆，其正视图是边长为6 m的正三角形ABC，粮堆母线AC的中点P处有一老鼠正在偷吃粮食，此时，小猫正在B处，它要沿圆锥侧面到达P处捕捉老鼠，则小猫所经过的最短路程是 m．(结果不取近似值)
二、选择题：（每题3分，共21分）
15. 下列各式中的最简二次根式是 （ ）
A . 
B . 
C. 
D . 
16. 若关于x的方程 x2+2x+k=0有两个相等的实数根，则k满足 （ ）
A. k>1 B. k≥1 C. k=1 D. k<1
17. 已知圆 ⊙O1 与 圆 ⊙O2 内切，它们的半径分别为 2和3，则这两个圆的圆心距d满足 （ ）
A. d=5 B. d=1 C. 1<d<5 D. d>5
18. 下列事件中是必然事件的是 （ ）
A. 我市2005年7月8日的最高气温是48 ℃
B. 我市夏季的平均气温比冬季低
C. 我市夏季的平均气温比冬季高
D. 我市 2006年12月24日将下雪。
19. 下列说法正确的是 ( )
A. 了解一批枪弹的杀伤半径可以采用普查
B. 了解一批种子的发芽率可以采用抽样调查
C. 了解无锡站一天的火车进出情况可以抽查
D. 检查一批日光灯的使用寿命可以采用普查。
20.某城市进行旧城区人行道的路面翻新，准备对地面密铺彩色地砖，有人提出了4种地砖的形状供设计选用：①正三角形 ②正四边形 ③正五边形 ④正六边形 其中不能进行密铺的地砖的形状是 （ ）
A. ① B. ② C. ③ D. ④
21. 下图是由一些相同的小正方形构成的几何体的三视图，在这个几何体中，小正方形的个数是 （ ）
正视图 左视图 俯视图
A. 4个 B. 5个 C. 6个 D. 7个
三、解答题：
22．（每题4分，共8分）
（1）计算：÷（- 2）2－2-1＋
（2）解方程：
23．（本题6分）如图：在 △ABC 中，点D、E、F分别在AB、AC、BC上，DE∥BC， EF∥AB，且F是BC的中点，求证：DE =CF
24．（本题6分）在下面的网格图中按要求画出图形，并回答问题：
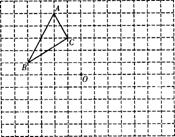
(1)先画出△ABC向下平移5格后的△A1B1C1，再画出△ABC以点O为旋转中心，沿顺时针方向旋转90°后的△A2B2C2；
(2)在与同学交流时，你打算如何描述(1)中所画的△A2B2C2的位置?
25. （本题8分）依据闯关游戏规则，请你探究“闯关游戏”的奥秘：
（1）用列表的方法表示有可能的闯关情况；
（2）求出闯关成功的概率.
26．（本题7分）某汽车停车场预计“十·一”国庆节这天将停放大小汽车1200辆次，该停车场的收费标准为：大车每辆次10元，小车每辆次5元．根据预计，解答下面的问题：
(1) 写出国庆节这天停车场的收费金额y(元)与小车停放辆次x(辆)之间的函数关系式，并指出自变量x的取值范围；(2)如果国庆节这天停放的小车辆次占停车总辆次的65％～85％，请你估计国庆节这天该停车场收费金额的范围．
27、（本题10分）（1）做一做：用四块如图l的瓷砖拼成一个正方形，使拼成的图案成轴对称图形．请你在图2、图3、图4中各画出一种拼法(要求三种拼法各不相同，所画图案中的阴影部分用斜线表示)
 |
（2）读一读：
式子“1十2＋3＋4＋5＋…＋100”表示从l开始的100个连续自然数的和。由于上述式子比较长，书写也不方便，为了简便起见，我们可以将“l＋2＋3＋4＋5＋…＋100”表示为
，这里“∑”是求和符号。例如：“1十3十5十7十9＋…＋99”(即从l开始的100以内的连续奇数的和)可表示为
；又如“l3十23＋33＋43＋53十63＋73＋83＋93＋103”可表示为
。同学们，通过对以上材料的阅读，请解答下列问题：①2十4十6十8十10＋……＋100(即从2开始的100以内的连续偶数的和)用求和符号可表示为
；②计算：
＝
(填写最后的计算结果)。
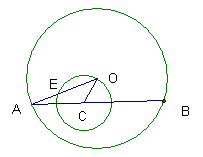28．（本题8分）如图，已知⊙O的半径OA=，弦AB=4，点C在弦AB上，以点C为圆心，CO为半径的圆与线段OA相交于点E。
（1） 求cosA的值；
（2） 设AC=x,OE=y,求y与x之间的函数解析式，并写出x的取值范围；
（3） 当点C在AB上运动时，⊙C是否可能与⊙O相切？如果可能，请求出当⊙C与⊙O相切时的AC的长；如果不可能，请说明理由。
29．（本题9分）已知∠AOB=90°，OM是∠AOB的平分线，按以下要求解答问题：
（1）将三角板的直角顶点P在射线OM上移动，两直角边分别与边OA、AB交于点C、D。①证明：PC=PD；②点G是CD与OP的交点，且PG =
PD，求△POD与△PDG的面积之比。
（2）将三角板的直角顶点P在射线OM上移动，一直角边与边OB交于点D，OD=1，另一直角边与直线OA、直线OB分别交于点C、E，使以P、D、E为顶点的三角形与△OCD相似，试求OP的长。
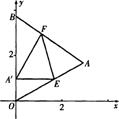
30．（本题9分）如图，△OAB是边长为2+
的等边三角形，其中O是坐标原点，顶点B在y轴的正方向上，将△OAB折叠，使点A落在边OB上，记为A/，折痕为EF．
(1)当A/E∥x轴时，求点A/和E的坐标；
(2)当A/E∥x轴，且抛物线y=-
x2+bx+c经过点A/和E时，求该抛物线与x轴的交点的坐标；
(3)当点A/在OB上运动但不与点O、B重合时，能否使△A/EF成为直角三角形?若能，请求出此时点A/的坐标；若不能，请你说明理由．
