一元二次方程与二次函数

一元二次方程与二次函数

①抛物线与x轴的两个交点在正半轴上一元二次方程有两个正实根；与x轴的两个交点在负半轴上一元二次方程有两个负根；与x轴的两个交点分布在原点两侧一元二次方程有一正一负的两个根；

②如果一元二次方程中的字母系数为整数时，可根据判别式建立关于这个字母的不等式并求整数解；

③题中遇到两解问题取舍时，要有充分的理由，不能凭主观意念来取舍。

例1：设x₁、x₂是方程的两个实数根。

(1)若，求y与m之间的函数关系式及自变量m的取值范围；

(2)画出第(1)题中函数y的图象，观察图象，说明函数y有没有最小值或最大值，如果有，求出最大值或最小值；如果没有，说明理由。

例2：已知抛物线和直线，它们的一个交点的纵坐标为4。

①求抛物线和直线的解析式；

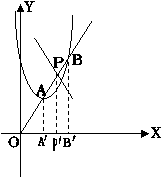
②如图，直线与①中的抛物线交于两个不同的点A、B，与①中的直线交于点P，分别过A、B、P作x轴的垂线，设垂足分别为A′、B′、P′，试用含有k的代数式表示，并证明。

③在②中能否适当选取k的值，使AA′＋BB′＝8？如果能，求出此时的k值；如果不能，请说明理由。

例3：已知抛物线。

①若抛物线与x轴只有一个交点，求m的值；

②若抛物线与直线只有一个交点，求m的值。

例4：已知二次函数中，m为不小于0的整数，其图象与x轴交于A、B两点，点A在原点左边，点B在原点右边。

(1)求这个二次函数的解析式；

(2)一次函数的图象过点A，与这个二次函数的图象交于点C，且S_△ABC＝10，

求一次函数的解析式。

例5：已知抛物线。

(1)求证：不论m取何实数时，抛物线与x轴的两个交点都在x轴的正半轴上；

(2)设抛物线与y轴交于点A，与x轴交于B、C两点(点B在点C的左侧)，求点A、B、C的坐标(用m的代数式表示)；

例6：已知抛物线经过点P(－3，4)以及P点关于坐标原点的对称点Q。

(1)求证：抛物线一定与x轴有两个不同的交点；

(2)设抛物线与x轴的两个交点为A、B，与y轴的交点为C。连结AC、BC，设∠CBA＝，∠CAB＝，

求证：、都为锐角；

(3)问是否有满足附加条件的抛物线存在？如果有，写出它的解析式；如果没有，请加以证明。

例7：如图，已知抛物线与x轴有两个交点A、B，且点A在x轴的正半轴上，点B在x轴的负半轴上，OA＝a，OB＝b。

(1)若a：b＝3：1，求m的值；

(2)由(1)求得的抛物线与y轴交于点C，问在抛物线上是否存在一点P，使△PAC≌△OAC？如果存在，求出点P的坐标；如果不存在，说明理由。

例题8：已知二次函数的图象与x轴交于A、B两点，其顶点为M，且△ABM为直角三角形，求m的值。

例题9：已知抛物线与y轴交于C点，与x轴交于A(x₁，0)，B(x₂，0)两点，x₁<x₂，，且S_△ABC＝6，求k的值。