用待定系数法求函数解析式1 姓名
一、填空题:
1、已知二次函数![]() 的图象与x轴只有一个交点,则m=
。
的图象与x轴只有一个交点,则m=
。
2、抛物线![]() 过点(1,0),与x轴两交点间距离为3,则b= ,c= 。
过点(1,0),与x轴两交点间距离为3,则b= ,c= 。
3、抛物线![]() 与x轴只有一个交点,则b= 。
与x轴只有一个交点,则b= 。
4、抛物线的顶点是C(2,![]() ),它与x轴交于A、B两点,它们的横坐标是方程
),它与x轴交于A、B两点,它们的横坐标是方程![]() 的两个根,则AB=
,S△ABC=
。
的两个根,则AB=
,S△ABC=
。
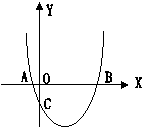
5、如图,二次函数![]() 的图象交x轴于A、B两点,交y轴于点C,当线段AB最短时,线段OC的长是
。
的图象交x轴于A、B两点,交y轴于点C,当线段AB最短时,线段OC的长是
。
 6、若抛物线
6、若抛物线![]() 的顶点在x轴上,则c的值是 。
的顶点在x轴上,则c的值是 。
7、抛物线![]() 与x轴有 个交点。
与x轴有 个交点。
二、选择题
1、抛物线![]() 与y轴的交点坐标是( )
与y轴的交点坐标是( )
(A)(0,-5);(B)(0,13);(C)(0,4);(D)(3,-5)
2、抛物线![]() 的顶点坐标为( )
的顶点坐标为( )
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D) (-1,0)
(D) (-1,0)
3、若抛物线![]() 的顶点在y轴上,则m的值为( )
的顶点在y轴上,则m的值为( )
(A)-3,(B)3,(C)-2,(D)2。
4、若抛物线![]() 的顶点在x轴上,则c的值为( )
的顶点在x轴上,则c的值为( )
(A) ![]() ;(B)
;(B) ![]() ; (C)
; (C) ![]() ;(D)
;(D) ![]()
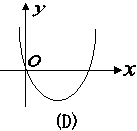
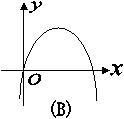
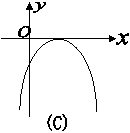 5、函数
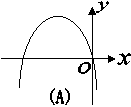
5、函数![]() 图象可能为( )
图象可能为( )
 | |||||
 | |||||
 | |||||
6、若(2,5),(4,5)是抛物线![]() 上的两点,那么它的对称轴为直线( )
上的两点,那么它的对称轴为直线( )
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
7、抛物线![]() 与x轴的交点个数是( )
与x轴的交点个数是( )
(A)0;(B)1;(C)2;(D)无数个。
三、求符合条件的二次函数式:
1、图象经过点(0,1),(1,1),(-1,-1)
2、对称轴是直线x=2,图象经过(1,4)和(5,0)两点。
3、抛物线与x轴的一个交点(6,0),顶点是(4,-8)
4、x=3时,y有最大值为-1,且抛物线过点(4,-3)。
5、抛物线以点(-1,-8)为顶点,且与y轴交点纵坐标为-6。
6、顶点在x轴上,对称轴方程x=-3,且经过点(-1,4)。
7、求二次函数![]() 的图象与x轴两交点间的距离的最小值,此时m的值是多少?
的图象与x轴两交点间的距离的最小值,此时m的值是多少?
8、二次函数图象经过A(0,2)和B(5,7)两点,且它的顶点在直线y=-x上。