圆单元测试

圆单元测试　　姓名　　　

一、选择题（每题4分，共36分）

1．我国主要银行的商标设计基本上都融入中国古代钱币的图案，下列我国四大银行的行标图案中的是轴对称而不是中心对称图形的是（　）

　　　

A　　　　　　  B　　　　　　　  C　　　　　　　　　 D

2．直角坐标系中，圆心O的坐标是（2，0），半径是4，则点P（－2，1）与⊙O的位置关系是（　 ）

A．点P在圆上　　B．点P在圆内　　C．点P在圆外　　D．不能确定

3．用两张全等的矩形纸片分别卷成两个形状不同的柱面（圆柱的侧面），设较高圆柱的侧面积和底面半径分别为S₁和r₁，较矮圆柱的侧面积和底面半径分别为S₂和r₂，那么（　 ）

A．，　　B．，　　

C．，　　D．，

4．已知⊙O₁和⊙O₂的半径分别为3cm和4cm，圆心距O₁O₂＝6cm，那么⊙O₁和⊙O₂的位置关系是（　 ）

A．内切　　B．相交　　C．外切　　D．外离

5．在△ABC中，AB＝3，AC＝4，BC＝5，把△ABC绕直线AC旋转一周得到一圆锥，其表面积为S₁；把△ABC绕直线AB旋转一周得到另一个圆锥，其表面积为S₂，则S₁/S₂等于（　 ）

A．　　 B．　　C．　　D．

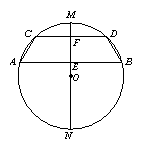
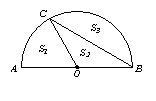
6．如图，AB为半圆O的直径，C为半圆上一点，且弧AC为半圆的1/3。设扇形AOC、△COB、弓形BmC的面积分别为S₁、S₂、S₃，则下列结论正确的是（　 ）

A．　　B．　　C．　　D．

7．如图，在⊙O中，弦AB∥CD，直径MN⊥AB且分别交AB、CD于点E、F，下列4个结论：①AE＝EB，②CF＝FD，③AC＝BD，④MF＝FE；其中正确的有（　 ）

A．1个　　B．2个　　C．3个　　D．4个

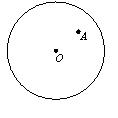
8．如图，A是半径为5的⊙O内一点，且OA＝3，过点A且长小于8的弦有（　 ）

得分　　　

A．0条　　B．1条　　C．2条　　D．4条

9．已知：点P到直线L的距离为3，以点P为圆心，r为半径画圆，如果圆上有且只有两点到直线L的距离均为2，则半径r的取值范围是（　 ）

A．　　B．　　C．　　D．

二、填空题（每题4分，共44分）

10．在同一平面内，1个圆把平面分成个部分，2个圆把平面最多分成个部分，3个圆把平面最多分成个部分，4个圆把平面最多分成个部分，那么10个圆把平面最多分成　　　 个部分。

11．圆周上有8个等分点，以其中三个为顶点的直角三角形共有　　　 个。

12．已知：半径为3的⊙O₁与半径为2的⊙O₂相切,则连心线O₁O₂＝　　　 。

13．在半径为5cm的圆内有两条互相平行的弦，一条弦长为8cm，另一条弦长为6cm，则这两条弦之间的距离是　　　　 。

14．一个圆锥的底面半径长为4cm，母线长为5cm，则圆锥的侧面积为　　　 。

15．某学校需修建一个圆心角为60⁰，半径为12m的扇形投掷场地，则该扇形场地的面积约为　　　 m²（取3.14，结果精确到0.1m²）

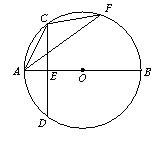
16．如图，△ACF内接于⊙O，AB是⊙O的直径，弦CD⊥AB于点E。CD＝BE＝8，则sin∠AFC＝　　　　。

17．已知扇形的弧长是2cm，半径为12cm，则这个扇形的圆心角是　　　　 。

18．⊙O₁、⊙O₂和⊙O₃是三个半径为1的等圆，且圆心在同一条直线上，若⊙O₂分别与⊙O₁、⊙O₃相交，⊙O₁与⊙O₃不相交，⊙O₁与⊙O₃的圆心距d的取值范围是　　　　  。

19．如图所示的曲边三角形右按下述方法作出：分别以正三角形的一个顶点为圆心，边长为半径，画弧使其经过另外两个顶点，然后擦去正三角形，三段圆弧所围成的图形就是一个曲边三角形。如果一个曲边三角形的周长为，那么它的面积为　　　　。

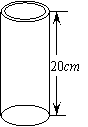20、如图所示，一种圆筒状包装的保鲜膜，其规格为“”，经测量这筒保鲜膜的内径r₁，外径r₂的长分别为3.2cm和4.0cm，则该种保鲜膜的厚度约为　　　　　 cm。（取3.14，结果保留两位有效数字）

三、解答题（第21、22、23、24题各8分，25、26题各10分，共52分）

21、阅读下面材料：

对于平面图形A，如果存在一个圆，使图形A上的任意一点到圆心的距离都不大于这个圆的半径，则称图形A被这个圆所覆盖。

对于平面图形A，如果存在两个或两个以上的圆，使图形A上的任意一点到其中某个圆的圆心的距离都不大于这个圆的半径，则称图形A被这些圆所覆盖。

例如：图1中的三角形被一个圆所覆盖，图2中的四边形被两个圆所覆盖。

回答下列问题：

⑴边长为1cm的正方形被一个半径为r的圆所覆盖，r的最小值是　　　cm；

⑵边长为1cm的等边三角形被一个半径为r的圆所覆盖，r的最小值是　　　；

⑶长为cm，宽为1cm的矩形被两个半径都为r的圆所覆盖，r的最小值是

　　  cm，这两个圆的圆心距是　　　  cm.

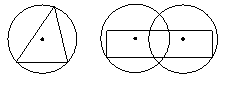　　图1　　　　　　 图2

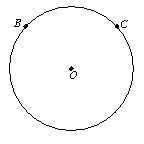
22、如图，已知B、C为⊙O上的两点。

求作：⊙O上一点P，使得PB＝PC。（保留作图痕迹，不写作法）

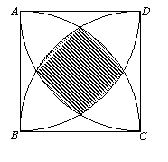
23、如图，正方形ABCD的边长为a，分别以四个顶点为圆心、边长为半径在正方形内作四条弧，求这四条弧所围成的阴影图形的周长和面积。

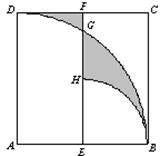
24、已知：如图，正方形ABCD的边长为2，以A为圆心，AB长为半径画BD，E、F分别是AB、CD的中点，EF交BD于点G，再以E为圆心，EB长为半径画弧，交EF于点H，求图中阴影部分的面积。

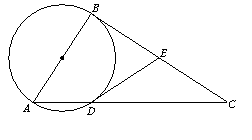
25、如图，已知：以Rt△ABC的直角边AB为直径作⊙O，与斜边AC交于点D，过点D作⊙O的切线交BC边于点E。

⑴试探求EB、EC、ED的关系，为什么？

⑵试问在线段DC上是否存在点F，满足？若存在，作出点F，并予以证明；若不存在，请说明理由。

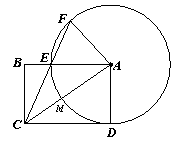26、如图，已知矩形ABCD，以A为圆心，AD为半径的圆交AC、AB于M、E，CE的延长线交⊙A于F，CM＝2，AB＝4.

⑴求⊙A的半径；

⑵求CE的长和△AFC的面积。