九年级数学测试题
一、 填空题：（每题4分，计20分）
1．已知等腰三角形一腰上的高等于腰长的一半，则这个三角形的底角为 。
2．某函数具有下列两条性质：①图象关于原点O成中心对称；②当x＞0时，函数y的值随自变量x的增大而增大。则此函数的表达式为 。（只要写出符合条件的一个）
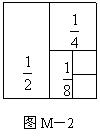
3．如图M－2，把一个面积为1的正方形等分成两个面积为
的矩形，接着把面积为的矩形等分成两个面积为
的矩形，再把面积为
的矩形分成两个面积为
的矩形……则计算：
。
4．某农场粮食产量在两年内从3000吨增加到3630吨，平均每年增长的百分率是 。
5．在一个有40万人口的县，随机调查了3000人，其中有2130人看中央电视台的焦点访谈，在该县随便问一个人，他看焦点访谈的概率大约是 。
二、选择题：（每题4分，计40分）
6.下列方程中，是一元二次方程的是（ ）
A. 
B.
C.
D.
7．下列方程有实数根的是（ ）
A． 
B.
C.
D. 
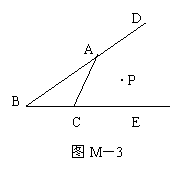
8．如图M－3，已知点P到BE,BD,AC的距离恰好相等，则点P的位置：①在∠B的平分线上；②在∠DAC的平分线上；③在∠ECA的平分线上；④恰是∠B,∠DAC,∠ECA三条角平分线的交点。上述结论中，正确结论的个数是（ ）
A. 1 B. 2 C. 3 D. 4
9．顺次连接四边形ABCD各边中点所成的四边形为菱形，那么四边形ABCD的对角线AC的BD的关系为（ ）
A. 相等 B. 互相垂直 C.相等且互相垂直 D.以上答案都不正确
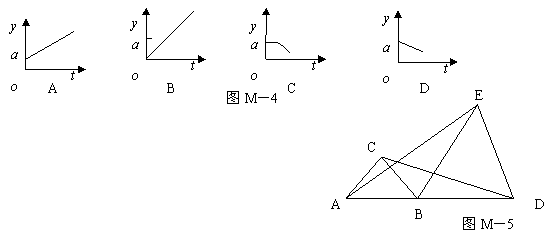
10．某工厂去年积压产品a件（ a＞0）,今年预计每月销售产品2b件（b＞0）,同时每月生产产品b件，如果产品积压量y（件）是今年开工时间t（月）的函数。在图M－4中，图象只能是（ ）
11．如图M－5，△ABC和△BDE都是等边三角形，AB＜BD，若△ABC不动，将△BDE绕点B旋
转，则在旋转过程中AE与CD的大小关系为 （ ）
A．AE=CD B. AE＞CD C. AE＜CD D. 无法确定
12.下列说法正确的个数是( )
①某人下午4点时的影长大于下午2点时的影长
②晚上人在路灯下行走时,人离路灯越远,影子就越短。
③甲、乙两人在太阳光下行走，同一时刻他们的身高
与影长的比相等。
A．3个 B. 2个 C. 1个 D. 0个
13. 在相同时刻的物高与影长成正比例,如果高为1.5米的测竿的影长为2.5米,那么影长为30米的旗杆的高是( ) A. 20米 B. 16米 C. 18米 D. 15米
14. 在同一平面直角坐标系中,正比例函数
与反比例函数
的图象大体位置不可能是图M－6中的( )
 |
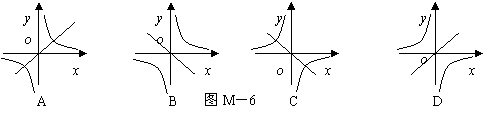15.在△ABC中,M是AB的中点,且AM=CM=BM,则△ABC是( )
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 等腰三角形
三﹑解答题(每小题8分,计32分)
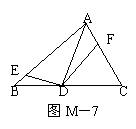16.如图M－7,△ABC中,AD是∠A的平分线,E,F分别为AB,AC上的点,且,∠AED+∠AFD=180°,求证:DE=DF.
17.如图M－8,在正方形ABCD中,F是CD上一点,E是BC延长线上一
点,且CE=CF,连接BF,DE,EF,求证:
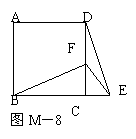⑴△BCF≌△DCE;
⑵若∠CDE=30°,求∠BFE的度数.
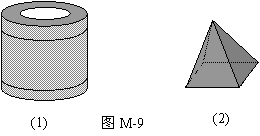
18.画出如图M－9中几何体的三种视图(右图为正四棱锥).
 |
19.⑴解方程
⑵运用配方法思想讨论:
有最大值还是有最小值,是多少?(其中p、q为常数)
四、(每题10分,计20分)
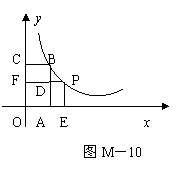20.正方形OABC的面积为9,A点在x轴上,C点在y轴上,点B在
(k＞0,x＞0)的图象上(图M－10),点P(m,n)是的图象上任一点,过点P分别作x轴,y轴的垂线PE,PF,垂足为E,F.设矩形OEPF和正方形OABC重合部分面积为S.⑴求点B的坐标及k的值;⑵当
时,求P点的坐标;⑶试写出S关于m的函数关系式.
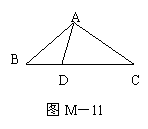
21.已知△ABC是等腰直角三角形(图M－11),请根据要求解答下列问题:⑴
若把△ABD沿直线AD折叠,请画出折叠后的△ADF;⑵折叠AC,使AC与AF重合,找出折痕与BC的交点E,并说明C点与F点是否重合;⑶试判断△DFE是什么形状的三角形,并证明你的理由.(所有作图,均写作法)
五.(每题12分,计24分)
22.启明公司生产某种产品,每件产品成本为3元,售价是4元,年销售量为10万种,为了获得更好的利益,公司准备拿出一定的资金做广告,根据经验,每年投入的广告费用为x万元时,产品的销售将是原来售量的y倍,且
,若把利润看成是销售总额减去成本费和广告费,要使公司年利润达到16万元,投入的广告费应为多少万元?
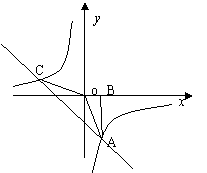23.如图:Rt△ABO的顶点A是双曲线与直线
在第四象限的交点,AB⊥x轴于B,且S△ABO=
⑴求这两个函数的解析式. ⑵求直线与双曲线的两个交点A,C的坐标和△AOC的面积.
六.(第1题6分,第2题8分,计14分)
24.同时转动如图6－3中的两个转盘,
当转盘停止转动时,指针所指的颜色相
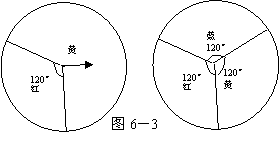同的概率是多少?(用列表法)
25．如图3－2－38，图形的操作过程（本题中四个
矩形的水平方向的边长均为a,坚直方向的边长均为
b）；在图3－2－38（1）中，将线段A1A2向右平移
1个单位到B1B2得到封闭图形A1A2B2B1（即阴影部
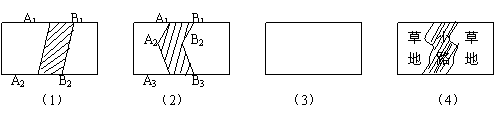分）；在图3－2－38（2）中，将折线A1A2A3向右平移1个单位得到B1B2B3，得到封闭图形A1A2A3
B3 B2 B1（即阴影部分）
（1）在图3－2－38（3）中请你类似地画一条有两个折点的折线，同样向右平移1个单位，得到一个封闭图形，用斜线画出阴影；（2）请你分别写出上述三个图形中除去阴影部分后剩余图形的面积：S1= ；S2= ；S3= 。（3）联想与探索：如图3－2－38（4）在一块矩形草地上，有一条弯曲的柏油小路（小路任何地方的水平宽度都是1个单位）。请你猜想空白部分表示的草地面积是多少？并说明你的猜想是正确的。