九年级数学科期中考试试卷
| 题号 | 一 | 二 | 三 | 总分 | ||||||||
|
|
| 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | ||
| 得分 |
|
|
|
|
|
|
|
|
|
|
|
|
一、选择题（每题3分，共30分）
1.下列函数中，是反比例函数的是 （ ）
A、
B、
C、
D、
2.已知直线MN是线段AB的垂直平分线，下列说法正确的是 （ ）
A、与AB距离相等的点在MN上 B、与点A和点B距离相等的点在MN上
C、与MN距离相等的点在AB上 D、AB垂直平分MN
3.以下各组数为三边① 3，4，5 ② 10，12，13 ③ 5，12，13 ④ 3，5，7 ⑤9，40，41 其中能构成直角三角形的是 （ ）
A、①②③④⑤ B、①②③⑤ C、①③ D、①③⑤
4.下列命题中错误的是 （ ）
A、两条对角线互相平分的四边形是平行四边形 B、两条对角线相等的四边形是矩形
C、两条对角线互相垂直的矩形是正方形 D、两条对角线相等的菱形是正方形
5.到三角形三个顶点距离相等的点是 （ ）
A、三条中线的交点 B、三条角平分线的交点
C、三条高的交点 D、三边垂直平分线的交点
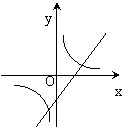6.在同一直角坐标系中，函数
的图象大致是 （ ）
 | |||||
 | |||||
| |||||
A B C D
7.三角形的一条中位线与第三边上的中线一定 （ ）
|
|
|
中，AC=BC，
|
|
|
|
交BC于D，
于点E，则AB与AC、CD之间的关系是（ ）
A、
B、AB=AC+CD C、AB<AC+CD
D、以上三种都有可能
9.三角形两边长分别是8和6，第三边是一元二次方程
的一个实数根，则该三角形的面积是
（ ）
A、24或8
B、24
C、48
D、8或22
10.已知方程
的两个实数根的平方和等于11，则k值 （ ）
A、k=-3或1 B、k=-3 C、k=1 D、k=3
二、填空题（每题4分，共32分）
11.方程
化成一般形式是
，二次项是
，一次项系数是
，常数项是
。
12.已知关于x的方程
，当n
时，它是一元二次方程。
13.若y=
是反比例函数，则k=
,它的图象在
象限。
14. 直角三角形中，
角所对的边长为8㎝，则斜边上的高为
㎝。
15.等腰三角形一边为2，一边为6，则其周长为 。
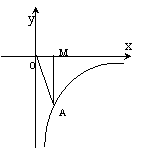
16.如图,点A是反比例函数
的图象上一点,AM垂直x轴于M, 
AOM的面积为2,则图中这支函数图象的解析式为 。
17. 用一块面积为900㎝2 的等腰梯形彩纸做风筝，用竹条做梯形的对角线，对角线互相垂直，那么用作两条对角线的竹条长应为 。
|
|
|
|
|
|
，N是AC上一动点，则DN+MN的最小值为
。
 |
|
|
| |||||||||
| ||||||||||||
|
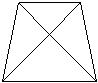
(第16题) (第17题) (第18题)
三、解答题。
19.解方程（8分） 20.用配方法解方程（不用配方法不给分）(8分)
21.（9分）水池内装有12
的水，如果从排水管中每小时流出x的水，则流过y小时就可以把水放完，⑴ y与x的函数关系式 ⑵ 画出函数的图象 ⑶ 当x=6时，求时间y的值。
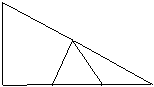
22.（10分）已知：在
中，
C=
，B=
，DE垂直平分AB，F是BD中点，
EF=4㎝，求AC的长度？
|
|
|
|
|
|
3.（10分）已知关于x的一元二次方程
有实数根，求：
（1）求m的取值范围。
（2）当m在取值范围内取最小正偶数时，求出该方程的根。
24.（10分）已知：四边形ABCD中，
于O，AC=12㎝，BD=8㎝，E，F，G，H分别是AB，BC，CD，DA的中点，求四边形EFGH的面积。
|
|
|
|
|
|
|
|
|
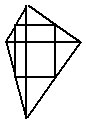
(第24题)
25.（10分）已知： ABCD中，E、F分别是BC、AD上的点，且BE=DF，G，H分别在CF、AE上的点，且CG=AH。求证：四边形HEGF是平行四边形。
|
|
|
|
|
|
|
|
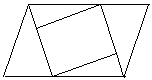
(第25题)
26.（10分）某商场在销售“才子”衬衫时，发现这种售价为200元/件的衬衫平均每天可售出20件，每件赢利40元，现商场决定采取换季打折出售，扩大销售量，尽量减少库存，经商场调查发现，如果每件降价4元，那么平均每天就可以多售出8件，⑴商场想平均每天在销售这种衬衫上赢利1200元，那么这种衬衫应打几折出售？⑵商场要想平均每天在销售这种衬衫上赢利最多，问商场应如何定价？最多赢利是多少？
27.（13分）已知反比例函数
和一次函数
，其中一次函数过（a,b），（a+1,b+k）两点，⑴ 求反比例函数的解析式；
⑵已知点A在第一象限内，且同时在上述两个函数的图象上，求点A的坐标；
⑶利用⑵的结论作答，请问：在x轴上是否存在一点P，是△POA为等腰三角形？若存在求P点坐标，若不存在请说明理由。