二次函数与几何

二次函数与几何

1、已知抛物线。

(1)求证：对于任何实数m，抛物线与x轴总有两个交点；

(2)若一次函数的图象与y轴交于点A，抛物线经过点B，且A、B两点关于x轴对称，求抛物线的解析式；

(3)在x轴的下方，(2)中所得的抛物线上，是否存在一点P，使S_△PAB＝3，若存在，给出证明；若不存在，请说明理由。

2、已知抛物线。

①求证：不论m取何值，抛物线与x轴必有两个交点，并且有一个交点是A(2，0)；

②设抛物线与x轴的另一个交点为B，AB的长为d，求d与m之间的函数关系式；

③设d＝10，P(a，b)为抛物线上一点，(i)当△ABP是直角三角形时，求b的值；(ii)当△ABP是锐角三角形、钝角三角形时，分别写出b的取值范围。(不必写出解答过程)

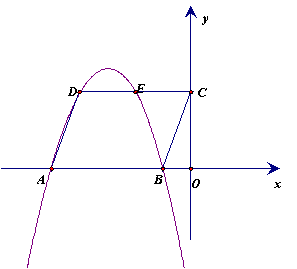
3、已知： ABCD在直角坐标系中的位置如图，O是坐标原点，OB：OC：OA＝1：3：5，S_ABCD=12，抛物线经过D、A、B三点。

①求A、C两点的坐标；

②求抛物线解析式；

③E是抛物线与DC交点，以DE为边的平行四边形，它的面积与S  _ABCD面积相等，且另两顶点中有一个顶点P在抛物线上。

求P点的坐标。

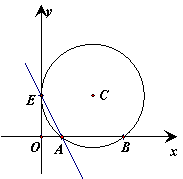4、如图，在直角坐标系中，点E和点A、B分别在y轴和x轴上，直线l₁：经过点E、A，以AB为弦的圆C与y轴相切于点E。

①求A、B两点的坐标；

②设抛物线经过点A、B，顶点为P，且

∠APB＝90⁰，求抛物线的解析式；

③过点A作直线l₂，使l₂⊥l₁，当a>0时，l₂与上述抛物线相交于点F，求S_△ABF。

5、已知直线交x轴于点A，交y轴于点B，抛物线过A、B两点及x轴上另一点C，且AC＝2。

(1)当∠BCO>∠BAO时，求抛物线的解析式；

(2)设点D的坐标为(－2，0)，试在线段AB上确定一点P，使△APD与△ABO相似，求P点的坐标；

(3)在(1)，(2)的条件下，在x轴下方的抛物线上是否存在点E，使△ADE的面积等于四边形APCE的面积？若存在，求E点的坐标；若不存在，请说明理由。

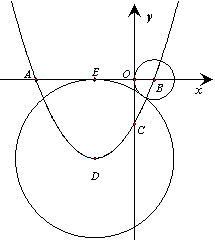6、抛物线与x轴交于A、B两点，与y轴交于C点，大圆圆心D是该抛物线顶点，小圆的圆心B是该抛物线与x轴正半轴的交点，大圆与x轴相切于E，小圆与y轴相切于O，两圆外切，且大圆半径为小圆半径的4倍。

(1)求ac＋b的值；

(2)当△ABC面积为时，求抛物线解析式。

7、已知：抛物线 (m≠－2)与y轴的交点为A，与x轴的交点为B、C两点(B点在C点的左边)

(1)写出A、B、C三点的坐标；

(2)设，试问是否存在实数a，使得△ABC为直角三角形？若存在，求出a的值；若不存在，请说明理由；

(3)设，当∠BAC最大时，求实数a的值。

8、已知：抛物线和直线。

它们的一个交点的纵坐标为4。

(1)求抛物线和直线的解析式；

(2)如图，直线 (k>0)与(1)中的抛物线交于两个不同的点A、B，与(1)中的直线交于点P，分别过A、B、P作x轴的垂线，设垂足分别为A^／，B^／，P^／。试用含有k的代数式表示，并证明。

(3)在(2)中能否适当选取k的值，使？如果能，求出此时的k值；如果不能，请说明理由。

9、一次函数的图象在第一、二、四象限内，且经过点(6，4)和(0，t)，与x轴交于点P，与直线交于点Q。

1、用含t的代数式表示点Q的纵坐标和△POQ的面积(O为坐标原点)

2、设△POQ的面积等于40。

(1)求：t的值，函数的解析式，点P、Q的坐标以及经过P、O、Q三点的抛物线的解析式；

(2)在如图所示的直角坐标系中，画出函数的图象和这条抛物线；

(3)在抛物线上是否存在点M，使得以点M为圆心的圆与函数的图象相切于点Q？如果存在，求出点M的坐标，如果不存在，试说明理由。