一、填空题：(每小题2分,共20分)
1、函数
是抛物线，则
＝ .
2、抛物线
与
轴交点为 ，与
轴交点为 .
3、二次函数
的图象过点（－1，2），则它的解析式是
，当 时，随的增大而增大.
4．抛物线
可由抛物线
向 平移 个单位得到．
5．抛物线
在轴上截得的线段长度是
．
6．抛物线
的图象经过原点，则
．
7．抛物线
，若其顶点在轴上，则 ．
8. 如果抛物线
的对称轴是x＝－2，且开口方向与形状与抛物线
相同，又过原点，那么a＝ ，b＝ ，c＝ .
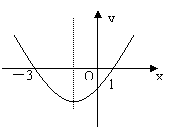
9、二次函数
的图象如下左图所示，则对称轴是
，当函数值
时，对应的取值范围是 .
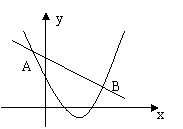
10、已知二次函数
与一次函数
的图象相交于点A（－2，4）和B（8，2），如上右图所示，则能使
成立的的取值范围
.
二、选择题：(每小题3分,共30分)
11.下列各式中,是的二次函数的是 ( )
A．
B．
C． 
D．
12．在同一坐标系中，作
、
、
的图象，它们共同特点是 ( )
A． 都是关于轴对称，抛物线开口向上 B．都是关于轴对称，抛物线开口向下
B． 都是关于原点对称，顶点都是原点
D．都是关于轴对称，顶点都是原点
13．抛物线
的图象过原点，则为（ ）
A．0 B．1 C．－1 D．±1
14．把二次函数
配方成顶点式为（ ）
A．
B． 
C．
D．
15．已知原点是抛物线
的最高点，则的范围是( )
A． 
B． 
C．
D．
16、函数
的图象经过点( )
A、（－1，1） B、（1 ，1） C、（0 , 1） D 、(1 , 0 )
17、抛物线
向右平移1个单位，再向下平移2个单位，所得到的抛物线是( )
A、
B、
C、
D、
18、已知
关于
的函数关系式
（ 
为正常数，为时间）如图，则函数图象为 ( )
h
h
h
h
o
o
t
t
o
t
o
t
A B C D
19、下列四个函数中, 图象的顶点在y轴上的函数是（ ）
A、
B、
C、
D、
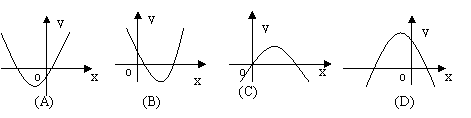20、已知二次函数
，若
，
，那么它的图象大致是（ ）
三、解答题：（共50分）
21(本题10分，每小题5分)、根据所给条件求抛物线的解析式：
（1）、抛物线过点（0，2）、（1，1）、（3，5）
（2）、抛物线关于轴对称，且过点（1，－2）和（－2，0）
22(本题10分)．已知二次函数
的图像经过A（0，1），B（2，－1）两点.
(1)求
和
的值； (2）试判断点P（－1，2）是否在此函数图像上？
23(本题10分)、某广告公司设计一幅周长为12米的矩形广告牌，广告设计费为每平方米1000元，设矩形一边长为米，面积为S平方米.
（1）
求出S与之间的函数关系式，并确定自变量的取值范围；
（2） 请你设计一个方案，使获得的设计费最多，并求出这个费用.
24(本题10分)、如图，抛物线
经过点A(1，0)，与y轴交于点B.
⑴求抛物线的解析式；
⑵P是y轴正半轴上一点，且△PAB是以AB为腰的等腰三角形，试求P点坐标.
 | |||
 | |||
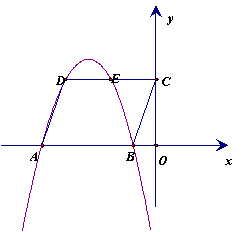
25(本题10分)、、已知： ABCD在直角坐标系中的位置如图，O是坐标原点，OB：OC：OA＝1：3：5，S ABCD＝12，抛物线经过D、A、B三点。
①求A、C两点的坐标；
②求抛物线解析式；
③E是抛物线与DC交点，以DE为边的平行四边形，它的面积与 ABCD 面积相等，且另两顶点中有一个顶点P在抛物线上.求P点的坐标.