初三年级质量检测（一）数学学科试卷
一，选择题：
1．一元二次方程3x2+4x－1=0的根的情况是（ ）
A;有两个不相等的实根 B; 有两个相等的实根 C;没有实数根 D;不能确定
2．已知正比例函数y=kx , y随着x的增大而增大，则一次函数 y=kx－2的图像不经过( )
A;第一象限 B; 第二象限 C; 第三象限 D; 第四象限
3．函数y=3x+1的图像一定经过点（ ）
A; (3,5) B;(－2,3) C; (2,7) D;(4,10)
4.菱形不一定具有的性质是（ ）
A;四条边相等 B;对角线互相垂直平分 C;对角线相等 D;内角和与外角和都等于3600
5．已知两圆半径分别为5和15，圆心距为26，那么一条外公切线的长为（ ）
A;8
B;16
C;5
D;24
6.正三角形的边心距与半径的比为（ ）
A;1:
B; 
C;1:2
D;
:2
7.一个圆锥的母线长为13，底面圆的半径长为5，则这个圆锥的侧面积为（ ）
A;65
B;90
C;130
D;200
8．某班七个合作学习小组人数如下：5，5，6，x，7，7，8已知这组数据的平均数是6，则这组数据的中位数是（ ）
A;5.5 B;6 C; 6.5 D;7
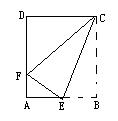
9.如图，将矩形ABCD沿CE折叠，点B恰好落在AD上，设此点为F，且AB:BC=4:5，则sin∠AFE的值是( )
A;
B;
C; 
D;
10.已知方程ax2+bx+c=0(a≠0)有两个实数根，下列结论，其中正确的有：（ ）
①若一个根为－1，则b=a+c
②若一个根为1，则另一个根为
③若两根互为相反数，则b=0
④若一个根大于1，另一根小于1，则
，
二，填空题：
11．已知0<X<3, 化简
的结果是
.
12.已知x1,x2是方程2x2+4x－3=0的两个根 则
.
13.在Rt△ABC中，点D,E分别在AB,AC上，DE∥BC,AB=6,AE=3,EC=2 则AD= .
14.已知数据组：7，8，9，10，11，12，13的样本方差是 。
15．如图AB是⊙O的直径，C,D是圆上两点,∠ADC=1100,则∠BAC= 度.
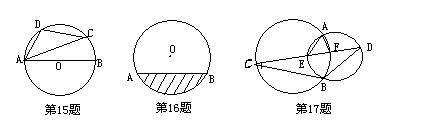
16.在直径为650mm的圆柱形油槽内装入一些油后，截面如图所示，若油面的宽AB=600mm，则油的最大深度为 mm。
17．已知⊙O1,⊙O2相交于A,B两点，直线CD依次交两圆于C,E,F,D，连结AE,AF,BC,BD，若∠EAF=550，则∠CBD= 度。
18．已知抛物线y=－x2+2(m+1)x+m+3与x轴的正半轴交于点A，与x轴的负半轴交于点B，且OA:OB=3:1，则m的值为 .
三，解答题：
19．解方程：
20．已知直线y=－x+3分别与x轴y轴交于A,B两点，二次函数y=ax2+bx+c的图像经过A,B两点和点C(1,1)
(1) 求这个二次函数的解析式。
(2) 先将（1）中所求出的二次函数的解析式配方，再写出抛物线的对称轴和顶点坐标。
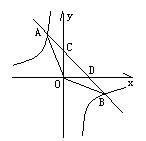
21．如图，反比例函数y=－
的图像与一次函数y=－x+2的图像交于A,B两点
（1） 求:A,B两点的坐标
（2） 求:△AOB的面积
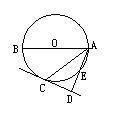
22.如图，已知AB是⊙O的直径，弦AC平分∠BAD，AD⊥CD于D,交于⊙O于E
（1） 判断直线CD是否与⊙O相切，并说明理由。
（2） 若AC=5,CD=3, 求DE的长
23.某企业储存煤炭350吨，为节能增效，企业改进了炉灶和燃煤技术，每天节约煤炭2吨，使储存的煤炭比原计划多用20天，求原来每天烧煤炭多少吨？
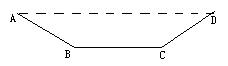
24．如图，引水渠的横断面为等腰梯形，渠深5米，渠底宽10米，斜坡AB与上口AD的夹角为300，
（1） 求水渠坡面AB的坡度及水渠上口AD的宽（结果精确到0.1米）
（2） 若水渠长2000米，计算此工程共挖土多少立方米。
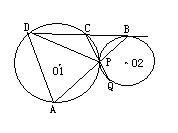
25.如图，⊙O1和⊙O2外切于点P，直线DCB切⊙O1于点B，交⊙O2于C,D，直线BP交⊙O2于点A，直线CP交⊙O1于点Q
（1） 求证：∠CBP=∠ADP
（2） 求证：AB2=AD2+BC·BD
（3）
设⊙O1的半径为r1，⊙O2的半径为R，BP=2,AD=4, 求:r : R的值。
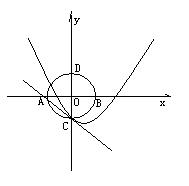
26．已知在平面直角坐标系中，半径为1的⊙O分别交x轴,y轴于A,B,C,D四点，抛物线y=x2+bx+c经过点C，且与直线AC只有一个公共点
（1） 求:直线AC的解析式
（2） 求:抛物线y=x2+bx+c的解析式
（3） 若点P是(2)中抛物线上的点，由点P作x轴的垂线，垂足为点Q，问：此抛物线上是否存在这样的点P，使△PQB∽△ADB?，若存在，求出点的坐标；若不存在，说明理由。
参考答案：
1.2.3.4.5.6.7.8.9.10.