中考数学模拟试题(二)
班级: 姓名: 座号: 评分:
一、填空题(每小题3分,共30分)
1、已知点P(-2,3),则点P关于x轴对称的点坐标是( )
2、据有关资料显示,长江三峡工程电站的总装机容量是千瓦,请你用科学记数法表示电站的总装机容量,应记为 千瓦
3、如图,要给这个长、宽、高分别为x、y、z的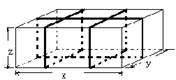 箱子打包,其打包方式如右图所示,则打包带的长至少要_________ (单位:mm)(用含x、y、z的代数式表示)
箱子打包,其打包方式如右图所示,则打包带的长至少要_________ (单位:mm)(用含x、y、z的代数式表示)
4、方程 x 2 = x 的解是__________________
5、圆内接四边形ABCD的内角∠A:∠B:∠C=2:3:4,则∠D=________°
6、已知一个梯形的面积为22![]() ,高为2 cm,则该梯形的中位线的长等于________cm
,高为2 cm,则该梯形的中位线的长等于________cm
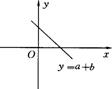 7、函数
7、函数![]() 的图像如图所示,则y随
的图像如图所示,则y随 ![]() 的增大而
的增大而
8、万州区某学校四个绿化小组,在植树节这天种下白杨树的棵数如 下:10,10,x,8,已知这组数据的众数和平均数相等,那么这组数据的中位数是 .
二、选择题(每小题3分,共15分)
9、下列方程中,属于一元一次方程的是( )
A、x=y+1 B、![]() =1 C、x2=x-1 D、x=1
=1 C、x2=x-1 D、x=1
10、已知 3-x+2y=0,则 2x-4y-3 的值为( )
A、-3 B、3 C、1 D、0
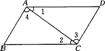 11、如图,∠1=∠2,则下列结论一定成立的是( )
11、如图,∠1=∠2,则下列结论一定成立的是( )
A AB∥CD B AD∥BC C ∠B=∠D D ∠3=∠4
12、把a3-ab2分解因式的正确结果是( )
A (a+ab)(a-ab) B a (a2-b2)
C a(a+b)(a-b) D a(a-b)2
13、在函数![]() 中,自变量
中,自变量![]() 的取值范围是( )
的取值范围是( )
A x≥2 B x>2 C x≤2 D x<2
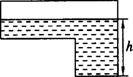
14、如图是某蓄水池的横断面示意图,分为深水池和浅水池,如果这个蓄水池以固定的流量注水,下面能大致表示水的最大深度h与时间t之间的关系的图像是( )
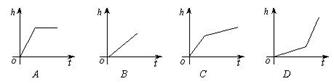
15、某校计划修建一座既是中心对称图形又是轴对称图形的花坛,从学生中征集到的设计方案有正三角形、正五边形、等腰梯形、菱形等四种图案,你认为符合条件的是( )
A 正三角形 B 正五边形 C 等腰梯形 D 菱形
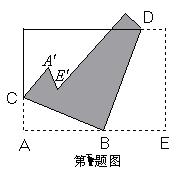
16、将一张长方形纸片按如图所示的方式折叠,BC、BD为折痕,则∠CBD的度数为( )
A.600 B.750 C.900 D.950
17、如果把中的x、y都扩大5倍,那么分式的值( )
A.扩大5倍B.不变C.缩小5倍D.扩大4倍
18、在△ABC和△A′B′C′中,①AB= A′B ′,③BC= B′C′,③AC= A′C′,④∠A=∠A′, ⑤∠B=∠B′,⑤∠C=∠C′.则下列条件中不能保证△ABC≌△A′B′C′的是( )
A.①②③ B.①②⑤ C.①⑤⑥ D.①②④
三、解答题(每小题6分,共24分)
19、计算:-22 + ()0 + 2sin30º
20、先化简,再求值:![]()
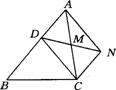 21、已知:如图,已知:D是△ABC的边AB上一点,CN∥AB,DN交AC于,若MA=MC,
21、已知:如图,已知:D是△ABC的边AB上一点,CN∥AB,DN交AC于,若MA=MC,
求证:CD=AN.
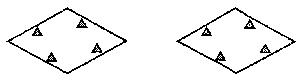
22、如图,菱形公园内有四个景点,请你用两种不同的方法,按下列要求设计成四个部分:⑴用直线分割;⑵每个部分内各有一个景点;⑶各部分的面积相等。(可用铅笔画,只要求画图正确,不写画法)
四、(20、21小题各7分,22、23小题各8分,共30分)
23、已知:反比例函数![]() 和一次函数
和一次函数![]() ,其中一次函数的图像经过点(k,5).
,其中一次函数的图像经过点(k,5).
(1) 试求反比例函数的解析式;
(2) 若点A在第一象限,且同时在上述两函数的图像上,求A点的坐标。
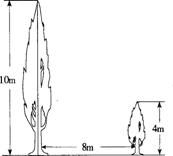
24.如图7,有两棵树,一棵高10米,另一棵高4米,两树相距8米. 一只小鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行多少米?
25、今年,我国政府为减轻农民负担,决定在5年内免去农业税.某乡今年人均上缴农业税25元,若两年后人均上缴农业税为16元,假设这两年降低的百分率相同.
(1)求降低的百分率;
(2)若小红家有4人,明年小红家减少多少农业税?
(3)小红所在的乡约有16000农民,问该乡农民明年减少多少农业税.
26、已知x1、x2是关于x的方程x2-6x+k=0的两个实数根,且x12x22-x1-x2=115,
(1)求k的值; (2)求x12+x22+8的值.
27.已知:如图9,等腰梯形ABCD的边BC在x轴上,点A在y轴的正方向上,A( 0, 6 ),D ( 4,6),且AB=![]() .
.
(1)求点B的坐标;
(2)求经过A、B、D三点的抛物线的解析式;
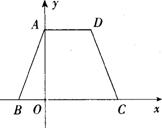 (3)在(2)中所求的抛物线上是否存在一点P,使得S△ABC = S梯形ABCD ?若存在,请求出该点坐标,若不存在,请说明理由.
(3)在(2)中所求的抛物线上是否存在一点P,使得S△ABC = S梯形ABCD ?若存在,请求出该点坐标,若不存在,请说明理由.