|
说明:本试卷共八大题,满分120分,考试时间120分钟.
请你认真审题,树立信心,沉着应答!
| 得分 | 评卷人 |
一、 填空题(本大题10小题,每小题2分,共20分)
1、计算:6-1= .
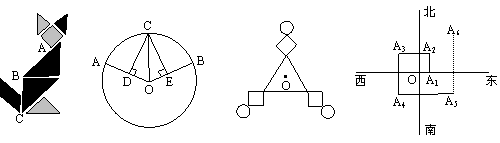
2、在七巧板拼图中(如图1),∠ABC= 度 .
3、“抛出的篮球会下落”,这个事件是 事件(填“确定”或“不确定”).
4、南宁国际会展中心是即将举办的中国—东盟博览会的会址,其总建筑面积为112100平方米,用科学记数法表示为________平方米(保留三个有效数字).
5、当x
时,分式![]() 有意义.
有意义.
![]()
![]() 6、如图2,D、E分别是⊙O的半径OA、OB上的点,CD⊥OA、CE⊥OB、CD=CE,则AC与CB两弧长的大小关系是:
.
6、如图2,D、E分别是⊙O的半径OA、OB上的点,CD⊥OA、CE⊥OB、CD=CE,则AC与CB两弧长的大小关系是:
.
7、写出一个图象位于一、三角限的反比例函数表达式
 |
8、顺次连接一个任意四边形四边的中点,得到一个___________四边形.
图1 图2 图3 图4
9、图3是两张全等的图案,它们完全重合地叠放在一起,按住下面的图案不动,将上面图案绕点O顺时针旋转,至少旋转______度角后,两张图案构成的图形是中心对称图形.
10、如图4,一个机器人从O点出发,图3向正东方向走3米到达A1点,再向正北方向走6米到达A2点,再向正西方向走9米到达A3点,再向正南方向走12米到达A4点,再向正东方向走15米到达A5点.按如此规律走下去,当机器人走到A6点时,离O点的距离是 米.______________
| 得分 | 评卷人 |
二、选择题(本大题8小题,每小题3分,共24分)每小题都给出
代号为(A)、(B)、(C)、(D)的四个结论,其中只有一个是正确的.选
择正确结论的代号填在括号内.
11.下列运算正确的是( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
12.分式![]() 计算的结果是( )
计算的结果是( )
 (A)
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
13.如图5,![]() 是平行四边形,则图中与
是平行四边形,则图中与![]() 相似的三角形
相似的三角形
共有( )
(A)1个 (B)2分
(C)3个 (D)4个
14.如图6,![]() 是
是![]() 斜边上的高,
斜边上的高,![]() ,则
,则
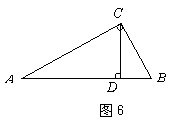
![]() 的值是( )
的值是( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
15.中央电视台“开心辞典”栏目有这么一道题:小兰从镜子中看到
挂在她背后墙上的四个时钟如下图所示,其中时间最接近四点钟
的是( )
 |
(A) (B) (C) (D)
16.如图7,分别以等腰直角三角板的直角边、斜边为旋转轴旋转,所形成的旋转体的全面
积依 次记为
次记为![]() ,则
,则![]() 的大小关系为( )
的大小关系为( )
(A)![]() (B)
(B)![]()
(C)![]() (D)无法判断
(D)无法判断
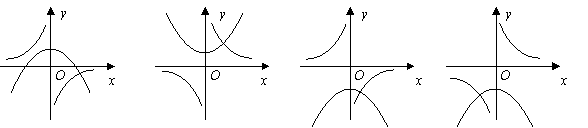 17.函数
17.函数![]() 与
与![]() 在同一直角坐标系中的图象可能是( )
在同一直角坐标系中的图象可能是( )
(A) (B) (C) (D)
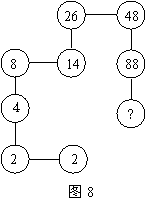
18.观察图8寻找规律,在“?”处填上的数字是( )
(A)128 (B)136
(C)162 (D)188
| 得分 | 评卷人 |
三、(本大题共2小题,每小题8分,满分16分)
19、(本题满分 8分)计算:(-2)3+![]() (2004-
(2004-![]() )0--
)0--![]()
20、(本题满分 8分)化简:![]()
| 得分 | 评卷人 |
四、(本题A类题满分7分,B类题满分10分)
21.本题有A、B两类题.A类题满分7分,B类题满分10分.请你选择其中一类证明.
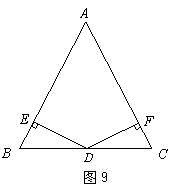
(A类)如图9,![]() .垂足分别为
.垂足分别为![]() .请你从下面三个条件
.请你从下面三个条件
中,再选出两个作为已知条件,另一个为结论,推出一个正确的命题(只需写出一种情
况).
①![]() ②
②![]() ③
③![]()
已知:![]() ,垂足分别为
,垂足分别为![]() , = , = .
, = , = .
 求证:
求证:
证明:
(B类)如图10,![]() ,请你从下面三个条件中,再选两个作为已知条件,另
,请你从下面三个条件中,再选两个作为已知条件,另
一个为结论,推出一个正确的命题(只需写出一种情况).
 ①
①![]() ②
②![]() ③
③![]()
已知:![]() , = , = .
, = , = .
求证:
证明:
友情提醒:若两题都做的同学,请你确认以哪类题记分,你的选择是 类题.
| 得分 | 评卷人 |
五、(本大题共6小题,每小题10分,共60分)
22、以下资料来源于2003年《南宁统计年鉴》
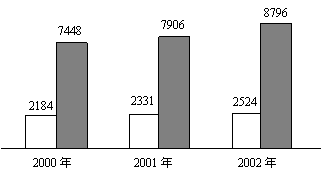 □表示南宁市农民人均纯收入(元)
□表示南宁市农民人均纯收入(元)
■表示南宁市城市居民人均可支配收入(元)
(1)分别指出南宁市农民人均纯收
入和城市居民人均可支配收入,
相对于上一年哪年增长最快?
(2)据统计,2000年~2002年南宁市农民年人均纯收入的平均增长率为7.5%,城市居民年人均可支配收入的平均增长率为 8.7%,假设年平均增长率不变,请你分别预计2004年南宁市农民人均纯收入和城市居民人均可支配收入各是多少?(精确到1元)
(3)从城乡年人均收入增长率看,你有哪些积极的建议?(写出一条建议)
23.如图11,石头![]() 和石头
和石头![]() 相距80cm,且关于竹竿l对称,一只电动青蛙在距竹竿30cm,
相距80cm,且关于竹竿l对称,一只电动青蛙在距竹竿30cm,
|
|
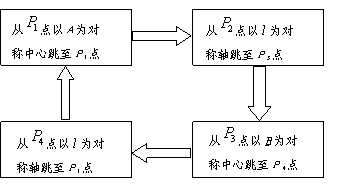 距石头A为60cm的
距石头A为60cm的
(1)
|
(2)
青蛙跳跃25次后停下,此时它与石头![]() 相距
相距
cm,与竹竿![]() 相距 cm.
相距 cm.
24、某饮料厂为了开发新产品,用A、B两种果汁原料各19千克、17.2千克,试制甲、乙两种新型饮料共50千克,下表是试验的相关数据:
(1)假设甲种饮料需配制x千克,请你写出满足题意的不等式组,并求出其解集.
| 饮料 每千克含量 | 甲 | 乙 |
| A(单位:千克) | 0.5 | 0.2 |
| B(单位:千克) | 0.3 | 0.4 |
(2)设甲种饮料每千克成本为4元,乙种饮料每千克成本为3元,这两种饮料的成本总额为y元,请写出y与x的函数表达式.并根据(1)的运算结果,确定当甲种饮料配制多少千克时,甲、乙两种饮料的成本总额最少?
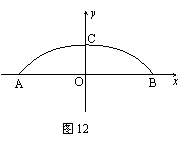
25、目前国内最大跨径的钢管混凝土拱桥——永和大桥,是南宁市又一标志性建筑,其拱形图形为抛物线的一部分(如图11),在正常情况下,位于水面上的桥拱跨度为350米,拱高为85米.
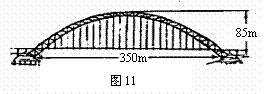 (1)在所给的直角坐标系中(如图12),假设抛物线的表达式为y=ax2+b,请你根据上述数据求出a、b的值,并写出抛物线的表达式(不要求写自变量的取值范围,a、b的值保留两个有效数字).
(1)在所给的直角坐标系中(如图12),假设抛物线的表达式为y=ax2+b,请你根据上述数据求出a、b的值,并写出抛物线的表达式(不要求写自变量的取值范围,a、b的值保留两个有效数字).
 |
(2)七月份汛期将要来临,当邕江水位上涨后,位于水面上的桥拱跨度将会减小 .当水位上涨 4 m 时,位于水面上的桥拱跨度有多大?(结果保留整数).
26.![]() 是一张放在平面直角坐标系中的矩形纸片,
是一张放在平面直角坐标系中的矩形纸片,![]() 为原点,点
为原点,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在
![]() 轴上,
轴上,![]() .
.
(1)
如图13,在![]() 上取一点
上取一点![]() ,使得
,使得![]() 沿
沿![]() 翻折后,点
翻折后,点![]() 落在
落在![]() 轴上,记作
轴上,记作![]() 点.求
点.求![]() 点的坐标;
点的坐标;
(2)
求折痕![]() 所在直线的解析式;
所在直线的解析式;
(3)
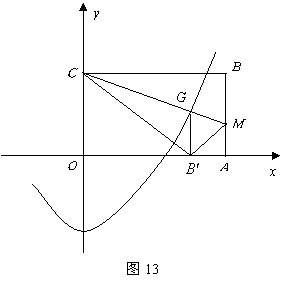 作
作![]() 交
交![]() 于点
于点![]() ,若抛物线
,若抛物线![]() 过点
过点![]() ,求抛物线的解析式,并判断以原点
,求抛物线的解析式,并判断以原点![]() 为圆心,
为圆心,![]() 为半径的圆与抛物线除交点
为半径的圆与抛物线除交点![]() 外,是否还有交点?若有,请直接写出交点的坐标.
外,是否还有交点?若有,请直接写出交点的坐标.
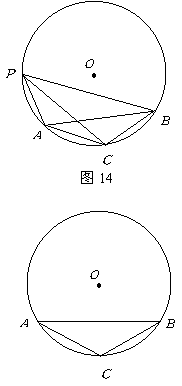
25、如图14,点![]() 是圆上的一个动点,弦
是圆上的一个动点,弦![]() 是
是![]() 的平分线,
的平分线,![]() .
.
(1)
当![]() 等于多少度时,四边形
等于多少度时,四边形![]() 有最大面积?最大面积是多少?
有最大面积?最大面积是多少?
(2)
当![]() 等于多少度时,四边形
等于多少度时,四边形![]() 是梯形?说明你的理由.
是梯形?说明你的理由.
 |
