中考数学模拟题-初中三年级数学试题练习、期中期末试卷、测验题、复习资料-初中数学试卷-试卷下载

中考数学模拟题

一、选择题（本题有7小题，每小题3分，共21分，每小题只有一个选项是正确的，不选、多选、错选均不给分）

1．-2的绝对值是（　　　）

　（A）-2　　　（B）2　　　（C）　　　（D）

2．下列运算正确的是（　　）

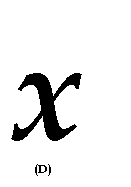　（A）　（B）　（C）　（D）

3．下列图形中，轴对称图形是（　　）

4．已知关于x的一元二次方程有实数根，则实数a的取值范围是（　　）

（A）a≤1　　 (B) a<1　　 (C) a≤-1　　 (D) a≥1

5．知点A（-2，y₁）、B（-1，y₂）、C（3，y₃）都在反比例函数的图象上，则（　　　）

（A）y₁<y₂<y₃　　 (B) y₃<y₂<y₁　　(C) y₃<y₁<y₂　　(D) y₂<y₁<y₃

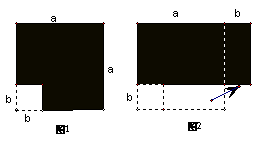
6．边长为a的正方形中挖去一个边长为b的小正方形（a>b）（如图1），把余下的部分拼成一个矩形（如图2），根据两个图形中阴影部分的面积相等，可以验证（　　）

（A）

（B）

（C）

（D）

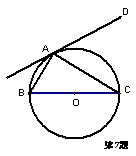
7．如图，已知BC是⊙O的直径，AD切⊙O于A，

　若∠C=40°，则∠DAC=（　　）

（A）50°　　（B）40°

（C）25°　　（D）20°

二、填空题（本题有10题，每小题4分，共40分）

8．的平方根是_______________

9．分解因式：=______________________

10．一只袋内装有2个红球、3个白球、5个黄球（这些球除颜色外没有其它区别），从中任意取出一球，则取得红球的概率是_____________

11．如图，ABCD是各边长都大于2的四边形，

分别以它的顶点为圆心、1为半径画弧（弧

的端点分别在四边形的相邻两边上），则这

4条弧长的和是________________

12．解是＿＿＿＿＿＿

13．“五一”黄金周期间，某风景区在7天假期中对每天上山旅游的人数统计如下表：

日期	5月1日	5月2日	5月3日	5月4日	5月5日	5月6日	5月7日
人数（万人）	1.2	1.2	2.3	1.8	1.8	1.2	0.8

　　这7天中上山旅游人数的众数是________万人，中位数是________万人。

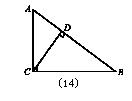
15. 如图，若CD是RtΔABC斜边上的高，AD=3，CD=4，则BC=__________ .

16．平移抛物线，使它经过原点，写出平移后抛物线的一个解析式____________________

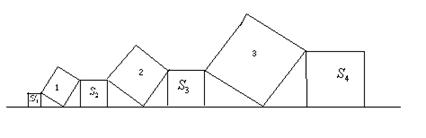17．在直线l上依次摆放着七个正方形(如图所示)。已知斜放置的三个正方形的面积分别是1、2、3，正放置的四个正方形的面积依次是S₁、S₂、S₃、S₄，则S₁＋S₂＋S₃＋S₄＝_________。

三、解答题（本题有9小题，共89分）以下各小题必须写出解答过程

18．（本题8分）计算：

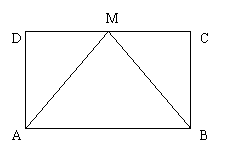
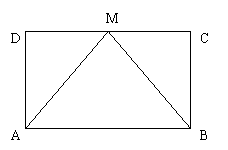
19．（本题8分）如图，矩形ABCD中，M是CD的中点。

求证：（1）△ADM≌△BCM；

　　（2）∠MAB=∠MBA

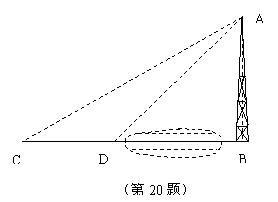
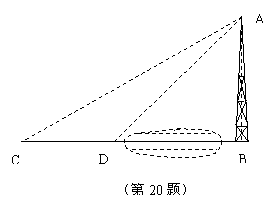
20．（本题9分）如图，河对岸有一铁塔AB。在C处测得塔顶A的仰角为30°，向塔前进16米到达D，在D处测得A的仰角为45°，求铁塔AB的高。

21．（10分）为响应承办“绿色奥运”的号召，某中学初三（2）班计划组织部分同学义务植树180棵，由于同学们参与的积极性很高，实际参加植树活动的人数比原计划增加了50%，结果每人比原计划少栽了2棵树，问实际有多少人参加了这次植树活动？

22．（8分）如图是一个木制圆盘,供甲、乙掷飞镖用.图中两同心圆,其中大圆直径为20cm,小圆的直径为10cm,若规定飞镖掷于小圆内(阴影部分),甲得2分,若飞镖掷于圆白菜环内(白色部分),乙得1分,最后按所得分数定输赢.

(1)你认为此游戏公平吗?通过计算说明理由.

(2)怎样修改得分规则,可以使游戏公平?

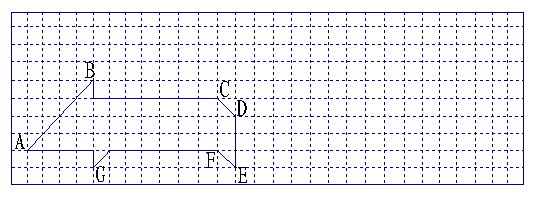23．（10分）下面的方格纸中，画出了一个“小猪”的图案，已知每个小正方形的边长为1．

（1）“小猪”所占的面积为多少？

（2）在上面的方格纸中作出“小猪”关于直线DE对称的图案（只画图，不写作法）；

（3）以G为原点，GE所在直线为x轴，GB所在直线为y轴，小正方形的边长为单位长度建立直角坐标系，可得点A的坐标是（_______，_______）．

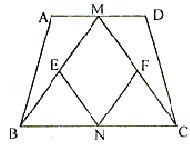
24．（12分）如图，在等腰梯形ABCD中，AD//BC，M、N分别为AD、BC的中点，E、F分别是BM、CM的中点。

　（1）求证：；

　（2）四边形MENF是什么图形？请证明你的结论；

　（3）若四边形MENF是正方形，则梯形的高与底边BC有何数量关系？并请说明理由。

25．（12分）在坐标平面内，半径为R的⊙C与x轴交于点D（1，0）、E（5，0），与y轴的正半轴相切于点A。点A、B关于x轴对称，点P（a，0）在x的正半轴上运动，作直线BP，作EH⊥BP于H。

（1）　　　求圆心C的坐标及半径R的值；

（2）　　　 △POB和△PHE随点P的运动而变化，若它们全等，求a的值；

（3）　　　若给定a=6，试判定直线BP与⊙C的位置关系（要求说明理由）。

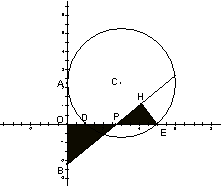
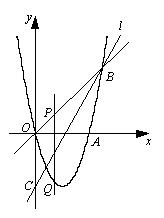26．（12分）如图，抛物线y＝ax²＋bx＋c经过点O（0，0），A（4，0），B（5，5）. 点C是y轴负半轴上一点，直线l经过B，C两点，且tan∠OCB＝.

（1）求抛物线的解析式；

（2）求直线l的解析式；

（3）过O，B两点作直线，如果P是直线OB上的一

个动点，过点P作直线PQ平行于y轴，交抛物

线于点Q. 问：是否存在点P，使得以P，Q，B

为顶点的三角形与△OBC相似？如果存在，请求

出点P的坐标；如果不存在，请说明理由.

数学中考模拟试卷

数学答题卡 　　成绩　　　　　　　 2006.05

一、选择题

（1）　　　　　　　　　（4）　　　　　　　　　（7）

（2）　　　　　　　　　（5）

（3）　　　　　　　　　（6）

二、填空题：

三、解答题：

（8）　　　　　　　（12）　　　　　　　　（16）　　　　　　　　

（9）　　　　　　　　 (13) 　　　　　　　　　　(17)　　　　　　　　　　

（10）　　　　　　　 (14)　　　　　　　　

(11)　　　　　　　 (15)　　　　　　　　

（18）（本题8分）