初三年级第一学期期中考试数学试卷A
本卷满分130分 用时120分钟
一、细心填一填(每空2分,共34分)
1.一种细菌的半径是0.000026m,用科学记数法表示这个数是 m.
2.分式![]() ,当 x=
时此分式值为0;当x=
时此分式无意义.
,当 x=
时此分式值为0;当x=
时此分式无意义.
3.设![]() 是方程
是方程![]() 的两根,则
的两根,则![]() =
,
=
,![]() =
.
=
.
4.因式分解![]() =
;方程
=
;方程![]() 的根为
.
的根为
.
5.已知![]() ,则
,则![]() =
.
=
.
6.已知方程![]() 的一根是
的一根是![]() ,则另一根为
;
,则另一根为
;![]() =
.
=
.
7.使得分式的值为正整数的整数a的值为 .
8.如果圆锥的母线长为6cm,底面圆半径为3cm,则这个圆锥的侧面积为 .
9.如图,⊙O是△ABC的外接圆,连接OA、OC,⊙O的半径R=2,sinB=![]() ,则弦AC的长为 .
,则弦AC的长为 .
10.如图,将正方形ABCD中的△ABP饶点B顺时针旋转能与△CBP′重合,若BP=4,则点P所走过的路径长为 .
11.如图,AB为半圆直径,BC为切线,BE为弦,AC交半圆于点D,交BE于F点,已知AF=FC,BC=![]() AC=1,则图中阴影部分的面积为
.
AC=1,则图中阴影部分的面积为
.
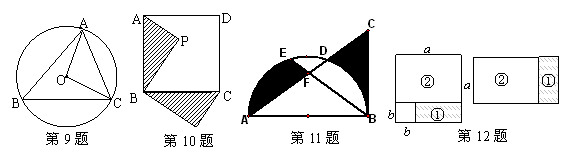
12.如图,在边长为![]() 的正方形的一角剪去一个边长
的正方形的一角剪去一个边长![]() 的正方形,再将剪下①与余下的部分②可以拼成一个长方形,这样我们可以得到一个公式
.
的正方形,再将剪下①与余下的部分②可以拼成一个长方形,这样我们可以得到一个公式
.
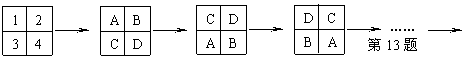 13.四个电子宠物排座位,A、B、C、D分别坐在1、2、3、4号座位上,以后它们不停的变换位置,第一次上下两排交换,第二次左右两列交换,第三次再上下两排交换,第四次再左右两列交换……(如图所示),这样一直下去,第2003次交换位置后,C在
号位置.
13.四个电子宠物排座位,A、B、C、D分别坐在1、2、3、4号座位上,以后它们不停的变换位置,第一次上下两排交换,第二次左右两列交换,第三次再上下两排交换,第四次再左右两列交换……(如图所示),这样一直下去,第2003次交换位置后,C在
号位置.
二、精心选一选(每题3分,共24分)
14.如果把分式![]() 中的x和y的值都扩大3倍,那么分式的
( )
中的x和y的值都扩大3倍,那么分式的
( )
(A)不变 (B)扩大3倍 (C)缩小3倍 (D)缩小6倍
15.若解分式方程=+1时可能会产生增根,则字母k的值为 ( )
(A)2 (B)6 (C)-6 (D)±6
16.如图所示的正四棱锥的俯视图是 ( )
 |
17.下列命题中,正确的命题是 ( )
(A)有两条边和其中一条边所对的角相等的两个三角形是全等三角形
(B)相似三角形面积之比等于相似比
(C)任意多边形的外角和都等于360°
(D)过切点的直线是圆的切线
18.关于![]() 的一元二次方程
的一元二次方程![]() 有实数根,则
有实数根,则![]() 的取值范围是 ( )
的取值范围是 ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
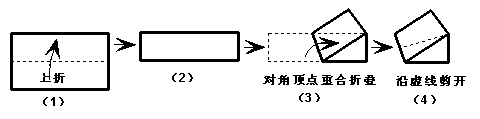 19.如图,小亮拿一张矩形纸图(1),沿虚线对折一次得图(2),下将对角两顶点重合折叠得图(3),按图(4)沿折痕中点与重合顶点的连线剪开,得到三个图形,这三个图形分别是
( )
19.如图,小亮拿一张矩形纸图(1),沿虚线对折一次得图(2),下将对角两顶点重合折叠得图(3),按图(4)沿折痕中点与重合顶点的连线剪开,得到三个图形,这三个图形分别是
( )
(A)都是等腰梯形 (B)两个直角三角形,一个等腰三角形
(C)两个直角三角形,一个等腰梯形 (D)都是等边三角形。
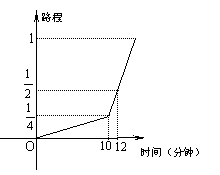 20.一名考生步行前往考场,10分钟走了总路程的
20.一名考生步行前往考场,10分钟走了总路程的![]() ,估计步行不能准时到达,于是他改乘租车赶往考场,他的行程与时间关系如图所示(假定总路程为1),则他到达考场所花的时间比一直步行提前了
( )
,估计步行不能准时到达,于是他改乘租车赶往考场,他的行程与时间关系如图所示(假定总路程为1),则他到达考场所花的时间比一直步行提前了
( )
(A)20分钟
(B)22分钟
(C)24分钟
(D)26分钟
21.已知点I是锐角△ABC的内心,A1、B1、C1分别是点I关于边BC、CA、AB的对称点.若点B在△A1B1C1的外接圆上,则∠ABC的度数是 ( )
(A)90° (B)60° (C)45° (D)30°
三、认真答一答
22.(每小题4分,共8分)计算:
(1)![]() 45°+
45°+![]() 0
(2)
0
(2)![]()
23.(每小题4分,共8分)
(1)解方程:(1)![]() (2)解方程
(2)解方程![]()
24.(6分)我市某中学对学生会倡导的“献爱心”捐款活动进行
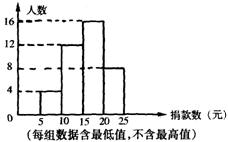 抽样调查,被调查的学生捐款情况如图所示。
抽样调查,被调查的学生捐款情况如图所示。
⑴该校共调查了______名学生.
⑵捐款15元以上(含15元)的学生频率是_______.
⑶若该校共有1800名学生,估计全校学生一共捐款至少
多少元?
25.(6分)已知:如图,正方形ABCD中,E为CD边上一点,F为BC延长线上一点,且CE=CF,
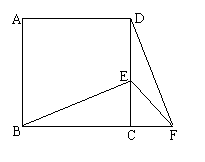 ⑴求证:△BCE≌△DCF;
⑴求证:△BCE≌△DCF;
⑵若∠FDC=30°,求∠BEF的度数.
26.(8分)如图,已知直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点A、B,与双曲线
轴分别交于点A、B,与双曲线![]() (
(![]() <0)分别交于点C、D,且C点的坐标为(
<0)分别交于点C、D,且C点的坐标为(![]() ,2).
,2).
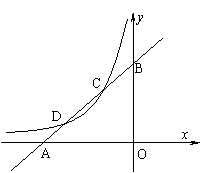 ⑴分别求出直线AB及双曲线的解析式;
⑴分别求出直线AB及双曲线的解析式;
⑵求出点D的坐标;
⑶利用图象直接写出:当x在什么范围内取值时,![]() >
>![]() .
.
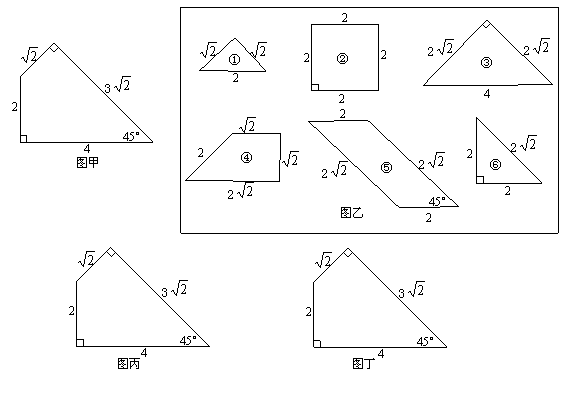
27.(6分)小明家用瓷砖装修卫生间,还有一块墙角面未完工(如图甲所示),他想在现有的六块瓷砖余料中(如图乙所示)挑选2块或3块余料进行铺设.请你帮小明设计两种不同的铺设方案(在下面图丙、图丁中画出铺设示意图,并标出所选用每块余料的编号)
28.(8分)阅读下列材料,解答问题.
饮水问题是关系到学生身心健康的重要生活环节,某中学共有教学班24个,平均每班有学生50人,经估算,学生一年在校时间约为240天(除去各种节假日),春、夏、秋、冬季各为60天.原来学生饮水一般都是购买纯净水(其他碳酸饮料或果汁价格更高),纯净水零售价为1.5元/瓶,每个学生春、秋、冬季平均每天要买1瓶纯净水,夏季平均每天要买2瓶纯净水.学校为减轻学生消费负担,要求每个班自行购买1台冷热饮水机,经调查,购买一台功率为500w的冷热饮水机约为150元,纯净水每桶6元.每班春、秋两季,平均每1.5天购买4桶,夏季平均每天购买5桶,冬季平均每天购买1桶,饮水机每天开10小时,当地民用电价为0.5元/度.
问题:⑴在未购买饮水机之前,全年平均每个学生要花费 元钱来购买纯净水饮用.
⑵请计算:在购买饮水机解决学生饮水问题后,每班当年共花费多少元?
⑶这项便利学生的措施实施后,该中学一年要为全体学生共节省多少元钱?
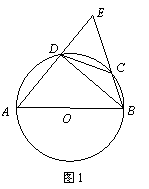 29.(10分)已知:如图1,在⊙O中,弦AB=2,CD=1,AD⊥BD.直线AD,BC相交于点E.
29.(10分)已知:如图1,在⊙O中,弦AB=2,CD=1,AD⊥BD.直线AD,BC相交于点E.
(1)求∠E的度数;
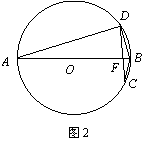 (2)如果点C,D在⊙O上运动,且保持弦CD的长度不变,那么,直线AD,BC相交所成锐角的大小是否改变? 试就以下三种情况进行探究,并说明理由(图形未画完整,请你根据需要补全).
(2)如果点C,D在⊙O上运动,且保持弦CD的长度不变,那么,直线AD,BC相交所成锐角的大小是否改变? 试就以下三种情况进行探究,并说明理由(图形未画完整,请你根据需要补全).
① 如图2,弦AB与弦CD交于点F;
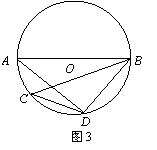 ② 如图3,弦AB与弦CD不相交;
② 如图3,弦AB与弦CD不相交;
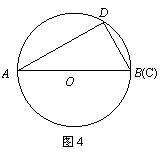 |
③ 如图4,点B与点C重合.
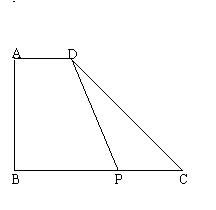
30.(12分)如图,在直角梯形ABCD中,AD∥BC,AD<BC,AB⊥BC,tan∠C=1,其中AD、BC是关于![]() 的一元二次方程
的一元二次方程![]() 的两根,且AB=
的两根,且AB=![]() ,点P在边BC上运动任(与B、C不重合).
,点P在边BC上运动任(与B、C不重合).
⑴求AB的长;
⑵设PC=x,四边形ABPD的面积为y,求y关于x的函数关系式,并写出自变量x的取值范围;
 ⑶若以D为圆心、
⑶若以D为圆心、![]() 为半径作⊙D,以P为圆心、以PC的长为半径作⊙P.当x为何值时,⊙D与⊙P相切?并求出这两圆相切时四边形ABPD的面积.
为半径作⊙D,以P为圆心、以PC的长为半径作⊙P.当x为何值时,⊙D与⊙P相切?并求出这两圆相切时四边形ABPD的面积.