初三年级第一学期数学期中试卷
一、细心填一填(每空2分,共34分)
1. 某种感冒病毒的直径是0.米,用科学记数法表示为_____________ 米.
2. 分式![]() ,当 x=
时此分式值为0;当x=
时此分式无意义.
,当 x=
时此分式值为0;当x=
时此分式无意义.
3.设![]() 是方程
是方程![]() 的两根,则
的两根,则![]() =
,
=
,![]() =
.
=
.
4.因式分解![]() =
;方程
=
;方程![]() 的根为
.
的根为
.
5.某汽车上山速度是![]() km/时,原路下山速度是
km/时,原路下山速度是![]() km/时,则上下山平均速度是______km/时。
km/时,则上下山平均速度是______km/时。
6.已知方程![]() 的一根是
的一根是![]() ,则另一根为
;
,则另一根为
;![]() =
。
=
。
7.使得分式的值为正整数的整数a的值为 。
8.如果圆锥的母线长为6cm,底面圆半径为3cm,则这个圆锥的侧面积为 。
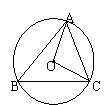
9.如图,⊙O是△ABC的外接圆,连接OA、OC,⊙O的半径R=2,sinB=![]() ,则弦AC的长为 。
,则弦AC的长为 。
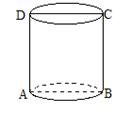
10.如图,已知圆柱体底面圆半径为![]() ,高为2,AB、CD分别是两底面直径,AD、BC是母线。若一只小虫从A点出发,绕侧面爬行到C点,则小虫爬行的最短路线的长度是
(结果用根号表示)
,高为2,AB、CD分别是两底面直径,AD、BC是母线。若一只小虫从A点出发,绕侧面爬行到C点,则小虫爬行的最短路线的长度是
(结果用根号表示)
|
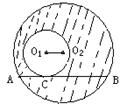
 11.如图⊙O1与⊙O2的弦AB切于点C,且O1O2∥AB,若AB=8,则阴影部分的面积为__________,若⊙O1的半径为2,⊙O2的半径为4,则扇形O2AB的周长为__________。
11.如图⊙O1与⊙O2的弦AB切于点C,且O1O2∥AB,若AB=8,则阴影部分的面积为__________,若⊙O1的半径为2,⊙O2的半径为4,则扇形O2AB的周长为__________。
|
| ||||
 12.英国的一位密码专家发明了一种密码,根据密码图1,则图2表示算式4×6÷2+7=19,请你仔细观察,则图3可表示的算式为
.
12.英国的一位密码专家发明了一种密码,根据密码图1,则图2表示算式4×6÷2+7=19,请你仔细观察,则图3可表示的算式为
.
二、精心选一选(每题3分,共24分)
13.如果把分式![]() 中的x和y的值都扩大3倍,那么分式的
( )
中的x和y的值都扩大3倍,那么分式的
( )
(A)不变 (B)扩大3倍 (C)缩小3倍 (D)缩小6倍
14.若解分式方程=+1时可能会产生增根,则字母k的值为 ( )
(A)2 (B)6 (C)-6 (D)±6
15.在下列四个图案中,既是轴对称图形,又是中心对称图形的是( )




(A) (B) (C) (D)
16.下列命题中,正确的命题是 ( )
(A)有两条边和其中一条边所对的角相等的两个三角形是全等三角形
(B)相似三角形面积之比等于相似比
(C)任意多边形的外角和都等于360°
(D)过切点的直线是圆的切线
17.关于![]() 的方程
的方程![]() 有实数根,则
有实数根,则![]() 的取值范围是 ( )
的取值范围是 ( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
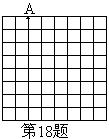 18.一只青蛙在如图8×8的正方形(每个小正方形的边长为1)网格的格点(小正方形的顶点)上跳跃,青蛙每次所跳的最远距离为
18.一只青蛙在如图8×8的正方形(每个小正方形的边长为1)网格的格点(小正方形的顶点)上跳跃,青蛙每次所跳的最远距离为![]() ,青蛙从点A开始连续跳六次正好跳回到点A,则所构成的封闭图形的面积的最大值是________。
,青蛙从点A开始连续跳六次正好跳回到点A,则所构成的封闭图形的面积的最大值是________。
(A)10 (B)8 (C)12 (D)9
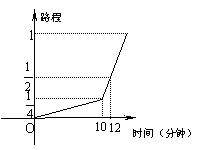 19.一名考生步行前往考场,10分钟走了总路程的
19.一名考生步行前往考场,10分钟走了总路程的![]() ,估计步行不能准时到达,于是他改乘租车赶往考场,他的行程与时间关系如图所示(假定总路程为1),则他到达考场所花的时间比一直步行提前了
( )
,估计步行不能准时到达,于是他改乘租车赶往考场,他的行程与时间关系如图所示(假定总路程为1),则他到达考场所花的时间比一直步行提前了
( )
(A)20分钟
(B)22分钟
(C)24分钟
(D)26分钟
20.已知点I是锐角△ABC的内心,A1、B1、C1分别是点I关于边BC、CA、AB的对称点.若点B在△A1B1C1的外接圆上,则∠ABC的度数是 ( )
(A)90° (B)60° (C)45° (D)30°
三、认真答一答
21.(每小题4分,共8分)计算:
(1)![]() 45°+
45°+![]() 0
(2)
0
(2)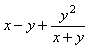
22.(每小题4分,共8分)
(1)解方程:(1)![]() (2)解方程
(2)解方程![]()
 23.(9分)如图9-(1)所示,把一张矩形纸片ABCD沿对角线BD折叠,将重合部分剪去,得到△ABF和△EDF.(1)试判断△ABF与△EDF是否全等?并加以证明.
23.(9分)如图9-(1)所示,把一张矩形纸片ABCD沿对角线BD折叠,将重合部分剪去,得到△ABF和△EDF.(1)试判断△ABF与△EDF是否全等?并加以证明.
|
|
|
 |  |  | |||
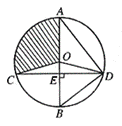
24.(8分)如图,已知⊙O的直径AB垂直于弦CD于E,连结AD、BD、OC、OD,且OD=5。(1)若![]() ,求CD的长;(2)若 ∠ADO:∠EDO=4:1,求扇形OAC(阴影部分)的面积(结果保留
,求CD的长;(2)若 ∠ADO:∠EDO=4:1,求扇形OAC(阴影部分)的面积(结果保留![]() )。
)。
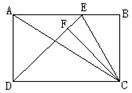
25.(8分)如图,在矩形ABCD中,对角线AC的长为10,且AB、BC(AB>BC)的长是关于![]() 的方程
的方程![]() 的两根。⑴求
的两根。⑴求![]() 的值;
的值;
⑵若E是AB上一点,CF⊥DE于F,求AE为何值时,△CEF的面积是△CED的面积的![]() 。
。
 |
26.(10分)市“健益”超市购进一批![]() 元/千克的绿色食品,如果以
元/千克的绿色食品,如果以![]() 元/千克销售,那么每天可售出
元/千克销售,那么每天可售出![]() 千克.由销售经验知,每天销售量
千克.由销售经验知,每天销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元)(
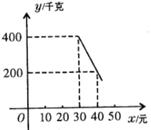
(元)(![]() )存在如下图所示的一次函数关系.(1)试求出
)存在如下图所示的一次函数关系.(1)试求出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)设“健益”超市销售该绿色食品每天获得利润![]() 元,当销售单价为何值时,每天可获得最大利润?最大利润是多少?
元,当销售单价为何值时,每天可获得最大利润?最大利润是多少?
(3)根据市场调查,该绿色食品每天可获利润不超过![]() 元,现该超市经理要求每天利润不得低于
元,现该超市经理要求每天利润不得低于![]() 元,请你帮助该超市确定绿色食品销售单价
元,请你帮助该超市确定绿色食品销售单价![]() 的范围(直接写出).
的范围(直接写出).
 |
27.(本题8分)
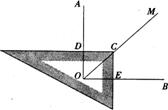
已知∠AOB=900,在∠AOB的平分线OM上有一点C,将一个三角板的直角顶点与C重合,它的两条直角边分别与OA、OB(或它们的反向延长线)相交于点D、E.
当三角板绕点C旋转到CD与OA垂直时(如图1),易证:OD+OE=OC.
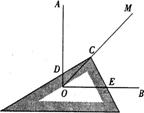
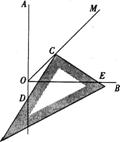
当三角板绕点C旋转到CD与OA不垂直时,在图2、图3这两种情况下,上述结论是否还成立?若成立,请给予证明;若不成立,线段OD、OE、OC之间又有怎样的数量关系?请写出你的猜想,不需证明.
|
|
|
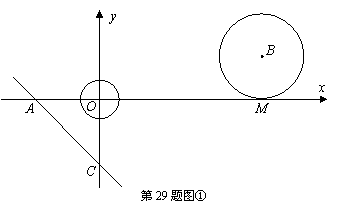
28.(本题13分)如图①,在平面直角坐标系中,以坐标原点O为圆心的⊙O的半径为![]() ,直线l:
,直线l:![]() 与坐标轴分别交于A、C两点,点B的坐标为(4,1),⊙B与x轴相切于点M。
与坐标轴分别交于A、C两点,点B的坐标为(4,1),⊙B与x轴相切于点M。
(1)求点A的坐标及∠CAO的度数;
![]() (2)⊙B以每秒1各单位长度的速度沿x轴负方向平移,同时,直线l绕点A顺时针匀速旋转。当⊙B第一次与⊙O相切时,直线l也恰好与⊙B第一次相切。问:直线AC绕点A每秒旋转多少度?
(2)⊙B以每秒1各单位长度的速度沿x轴负方向平移,同时,直线l绕点A顺时针匀速旋转。当⊙B第一次与⊙O相切时,直线l也恰好与⊙B第一次相切。问:直线AC绕点A每秒旋转多少度?
![]()
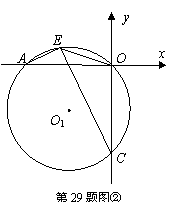 (3)如图②,过A、O、C三点作⊙O1,点E为劣弧AO上一点,连接EC、EA、EO,当点E在劣弧AO上运动时(不与A、O两点重合),
(3)如图②,过A、O、C三点作⊙O1,点E为劣弧AO上一点,连接EC、EA、EO,当点E在劣弧AO上运动时(不与A、O两点重合),![]() 的值是否发生变化?如果不变,求其值;如果变化,说明理由。
的值是否发生变化?如果不变,求其值;如果变化,说明理由。