中考数学冲刺模拟测试题（六）

中考数学冲刺模拟测试题（六）

一，填空题（每小题3分，共计21分）　　　　　　 姓名：　　　　　　　　  总分：　　　　 

1，－0.3的倒数是　　　　　 。　　　　　　 2，把527864保留三位有效数字是　　　　　　　  。

3，函数的自变量x的取值范围是　　　　　　　　　　　 。

4，直角三角形斜边上的高与中线分别是5㎝和6㎝，则它的面积是　　　　　 　　。

5，若方程x²－3x－1=0的两根是x₁，x₂，则=　　　　　　　　　  。

6，如图1，小张在打网球时，击球点距球网的水平距离为8米，已知网高0.8米，要使球恰好能打过网，而且落在离网4米的位置，则球拍击球时的高度h为　　　　　　　　   .  击球点

7，如图2，一个三角形ABC，（∠C=90°）绕斜边AB旋转一周，所得的

h m

几何体的剖面图是下面四个图形中的　　　　 。（填序号）

　 　　　　A

0.8 m

8m

4 m

落点

图1

C

图2　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　　　  B　　　　 ①　　　　　 ②　　　　　　 ③　　　　　 ④　　　　　　　　　　　　　　　　　　　　　　　　

二，选择题（每小题3分,共计24分）

8，计算的结果是（　　  ）A，－9a⁴　　 B，6a⁴　　C，9a⁴　　　 D，9a³　

9，已知a、b在数轴上上的位置如图所示，那么化简的结果是（　　  ）

　　a　　　b　　　0　　　　　　 A，2a　　　　 B，2b　　　　 C，－2a　　　　  D，－2b　　　　　　　　　　　

10，用10根等长的火柴棒拼成一个三角形（火柴棒不允许剩余、折断、重叠），这个三角形一定是（　　 ）　

A，等边三角形　　　　 B，等腰三角形　　　 C，直角三角形　　　　D，不等边三角形　

11，为了鼓励居民节约用水，政府出台新的居民用水收费标准：①若每月每户用水不超过4立方米，则按每立方米2元计算；②若每月每户居民用水超过4立方米，则超过部分按每立方米4.5元计算。现设该市居民某月用水x立方米，水费为y元，则y与x的函数关系式用图象表示正确的是（　　　）　　　

　　  y　　　　 　　　　　 y　　　　　　　　　　　  y　　　　　　　　　　　  y　　　　

　 8　　　　　　　　　  8　　　　　　　　　　　  8　　　　　　　　　　　  8　　　　　　　　　　　　　 

　　　　  4　　 x　 A　　　　 4　　  x　B　　　　　　 4　　 x　 C　　　　　　　4　　 x　 D　　　　　　　　　　 

12，某型号的手机连续两次降价，单台售价由原来的1185元降到580元，设平均每次降价的百分率为x，则列出方程正确的是（　　 ）　A，580（1＋x）²=1185　　B，1185（1＋x）²=580　

B

C

C，580（1－x）²=1185　　　　D，1185（1－x）²=580

13，某工件形状如图3所示，圆弧BC的度数为60°，AB=BC=6，∠BAC=30°，

图3

则工件的面积为（　　 ）　 A，6π　　B，4π　　C，8π　　 D，10π

A

14将函数y=x²＋6x＋7进行配方，正确的结果应为（　　　 ）

A，y=（x＋3）²＋2　　　　　 B，y=（x－3）²＋2

C，y=（x＋3）²－2　　　　　 D，y=（x－3）²－2　　

15，已知圆锥的底面直径为80㎝，母线长90㎝，则它的表面积为（　　　）㎝²。

A，3600π　　　　B，3600　　　 C，5200　　　　D，5200π

三，解答题（共75分）

16，（7分）化简求值：，其中x=。

17，（7分）解方程：。

18，（7分）如图，在梯形ABCD中，AD∥BC，AB=CD，BD⊥DC，且BD平分∠ABC，若梯形的周长为20㎝，求此梯形的中位线长。　　　　　　　　　　　　　　　　　　　　 A　　　　　　 D　　　　　　　

　　　　　　　　　　　　　　　　　  　　　　　　　　　　　　　B　　　　　　　　　　　　 C　　　　　

一个月内每天买进报纸份数	100	150
当月利润（单位：元）

19，（7分）某下岗工人在再就业中心扶持下，创办了一个报刊零售点，对经营的某种晚报这位再就业人员提供如下信息：①买进每份0.2元,卖出每份0.3元；②一个月内（以30天计）,有20天每天可卖出200份,其余10天每天只能卖出120份；③一个月内,每天从报社买进的报纸份数必须相同,当天卖不掉的报纸,以每份0.1元退还给报社.（1）填空表：

（2）设每天从报社买进该种晚报x份（120≤x≤200）时，月利润为y元，试求出y与x的函数关系式，并求出月利润的最大值。

　　　　　　　　　　　　　　　　　　

20，（8分）如图，某客机在海上失事，海上搜救中心立即通知位于A、B两处的专业救助轮甲和乙前往出事点协助搜救，接到通知后，甲轮测得出事地点C在A的南偏东60°，乙轮测得出事地点C在B的南偏东30°，已知B在A的正东方向，且相距100海里，分别求出这两艘船到达出事地点C的距离。

　　　　　　　　　　　　　　　　　　　　　　　　　　　 北　　　　　　　  北　　　　　　　　 

　　　　　　　　　　　　　　　　　　　　　　　　　 A　　　　　　　　　　 B　　　　

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 C　　　　

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 

 

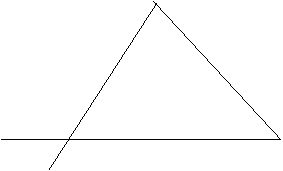
21，（9分）已知如图是某汽车行驶的路程S（千米）与时间t（分钟）的函数关系图。观察图中所提供的信息，解答下列问题。　　　　　　　　　　　　　　　　　　　  S（千米）　　

（1）汽车在前9分钟的平均速度是多少？　　　　　　　  40

12

（2）汽车在途中停了多长时间？　　　　　　　　　　　　　　 

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

0　　　9　　　16　　30　　　　t（分钟）

（3）当16≤t≤30时，求S与t的函数关系式。

22，（9分）某公司需在一个月（31天）内完成新建办公楼的装修工程，如果由甲、乙两工程队合做，12天可完成；如果由甲、乙两队单独做，甲队比乙队少用10完成。

（1），求甲、乙两工程队单独完成此项工程所需的天数；

（2）如果请甲工程队施工，公司每日需支付费用2000元；如果请乙队施工，公司每日需支付1400元，在规定时间内：A，请甲队单独完成此项工程；B，请乙队单独完成此项工程；C，请甲、乙队两队合作完成此项工程。以上三种方案哪一种花钱最少？

23，（10分）如图，已知PA切⊙O于点A，PBC是割线，弦CD∥AP，AD交BC于点E，点F在CE上，且ED²=EF·EC。

（1）求证：∠EDF=∠P；

A

O

F

E

C

（2）求证：CE·EB=EF·EP；

D

（3）若CE：EB=3：2，DE=6，EF=4，求PA的长。

24，（11分）已知抛物线的顶点在直线上，与x轴交于B（，0），C（，0）两点，其中＜，且。

（1）求这个函数的解析式；

P

B

（2）设这个抛物线与y轴交点为P，H是线段BC上一动点，过H作HK∥PB，交PC于K，连接PH，记线段BH的长为t，△PHK的面积S，试将S表示成t的函数。