二00七年高中阶段学校招生统一考试数学试卷
（满分100分，考试时间90分钟）
一、选择题（本大题8个小题，每小题3分，共24分）
1．计算
的结果是（ ）
（A） 0 (B) －2 （C） －4 (D) 4
2．下面调查中，适合做全面调查的是（ ）
(A)雪花牌电冰箱的市场占有率 (B)蓓蕾专栏电视节目的搜视率
(C)飞马牌汽车每百公里的耗油量 (D)今天班主任张老师与几名同学谈话
3．如图，立体图形由小正方体组成，这个立体图形中有小正方体（ ）
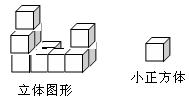(A) 9个
(B) 10个
(C) 11个 (D)12个
4．如果分式
的值为0，那么x为（ ）
(A) －2 (B) 0 (C) 1 (D) 2
5．一家鞋店在一段时间内销售了某种女鞋30双，各种尺码的销售如下表：
| 尺码/厘米 | 22 | 22．5 | 23 | 23．5 | 24 | 24．5 | 25 |
| 销售量/双 | 1 | 2 | 5 | 12 | 6 | 3 | 1 |
如果鞋店要购进100双这种女鞋，那么购进24厘米、24.5厘米和25厘米三种女鞋数量之和最合适的是（ ）
(A) 20双 (B)30双 (C)50双 (D)80双
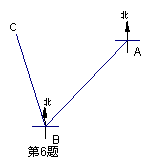
6．如图，一艘轮船由海平面上A地出发向南偏西40°的方向行驶40海里到达B地，再由B地向北偏西20°的方向行驶40海里达到C地，则A、C两地相距（ ）
(A)30海里 (B)40海里 (C)50海里 (D)60海里
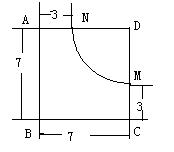
7．如图是一个零件示意图，A、B、C处都是直角，
是圆心角为90°的弧，其大小尺寸如图所示。则的长是（ ）
(A) 
(B)
(C)
(D)
8．如图是二次函数
图象的一部分，图象过点A（－3，0），对称轴为x＝－1。给出四个结论：①
＞4ac;②2a+b=0
;③a-b+c=0;④5a＜b。其中正确结论是（ ）
(A) ②④ (B) ①④ (C) ②③ (D) ①③
二、填空题（本大题共4个小题，每小题3分，共12分）
9．计算：
＝________________。
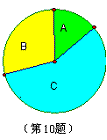10．据四川省统计信息网《2007年1季度四川民营经济发展状况分析》，2007年1季度四川民营经济增加分类统计如下表。根据此表作出的扇形统计图如图。请判断扇形统计图中对应
| 组别 | 增加值（亿元） |
| 第一产业 | 146．50 |
| 第二产业 | 521．39 |
| 第三产业 | 315．94 |
组别名称：
A对应_____________，B对应________，C对应___________。
11．已知反比例函数的图象经过（3，2）和（m，－2），则m的值是___________.
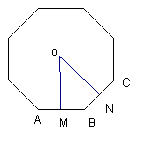
12．点M、N分别是正八边形相邻两边AB、BC上的点，且AM=BN，则∠MON＝_______度。
三、（本大题共2个小题，每小题6分，共12分）
13．化简：
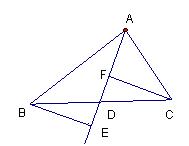
14．如图，已知BE⊥AD，CF⊥AD，且BE=CF，请判断AD是△ABC的中线还是角平分线？请说明你判断的理由。
四、（本大题共2个小题，每小题6分，共12分）
15．某商场举行“庆元旦，送惊喜”抽奖活动，10000个奖劵中设有中奖奖劵200个。
（1）小红第一个参与抽奖且抽取一张奖劵，她中奖的概率有多大？
（2）元旦当天在商场购物的人中，估计有2000人次参与抽奖，商场当天准备多少个奖品比较合适？
16．在一幅长8分米，宽6分米的矩形风景画（如图（1））的四周镶宽度相同的金色纸边，制成一幅矩形挂图（如图92）。如果要使整个挂图的面积是80平方米，求金色纸边的宽。
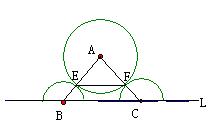17．如图是某城市一个主题雕塑的平面示意图，它由置放于地面l上两个半径均为2米的半圆与半径为4米的⊙A构成，点B、C分别是两个半圆的圆心，⊙A分别与两个半圆相切于点E、F，BC长为8米。求EF的长。
18．平面直角坐标系中，点A的坐标是（4，0），点P在直线y=－x＋m上，且AP=OP=4，求m的值。
19．某商店需要购进一批电视机和洗衣机，根据市场调查，决定电视机进货量不少于洗衣机进货量的一半。电视机与洗衣机的进价和售价如下表：
| 类别 | 电视机 | 洗衣机 |
| 进价（元/台） | 1800 | 1500 |
| 售价（元/台） | 2000 | 1600 |
商店计划购进电视机和洗衣机共100台，最多可筹集资金161800元。
（1） 请你帮助商店算一算有多少种进货方案？（不考虑除进价之外的其它费用）
（2） 哪种进货方案待商店销售完购进的电视机与洗衣机后获得利润最多？并求出最多利润，（利润＝售价－进价）
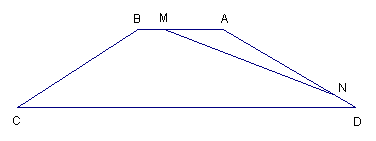
20．如图，等腰梯形ABCD中，AB=15,AD=20,∠C＝30°，点M、N同时以相同的速度分别从点A、点B开始在AB、AD（包括端点）上运动。
（1）设ND的长为x，用x表示出点N到AB的距离，并写出x的取值范围。
（2）当五边形BCDNM面积最小时，请判断△AMN的形状。
八、（本题满分8分）
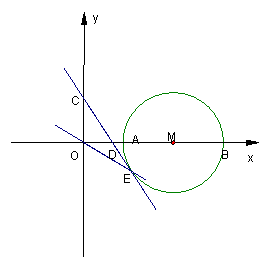21、如图，点M（4，0），以点M为圆心。2为半径的圆与x轴交于点A、B。已知抛物线
过点A和B，与y轴交于点C。
（1）求点C的坐标，并在图中画出抛物线的大致图象；
（2）点Q（8，m）在抛物线上，点P为此抛物线对称轴上一个动点，求PQ＋PB的最小值。
（3）CE是过点C的⊙M的切线，点E是切点，求OE所在直线的解析式。