第26章 二次函数单元检测 (A) 姓名___ ____
一、填空题：
1、函数
是抛物线，则
＝ .
2、抛物线
与
轴交点为 ，与
轴交点为 .
3、二次函数
的图象过点（－1，2），则它的解析式是
，
当 时，随的增大而增大.
4．抛物线
可由抛物线
向 平移 个单位得到．
5．抛物线
在轴上截得的线段长度是
．
6．抛物线
的图象经过原点，则
．
7．抛物线
，若其顶点在轴上，则 ．
8. 如果抛物线
的对称轴是x＝－2，且开口方向与形状与抛物线
相同，又过原点，那么a＝ ，b＝ ，c＝ .
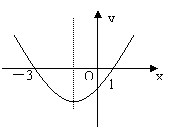
9、二次函数
的图象如下左图所示，则对称轴是
，当函数值
时，
对应的取值范围是 .
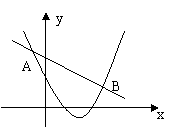
10、已知二次函数
与一次函数
的图象相交于点
A（－2，4）和B（8，2），如上右图所示，则能使
成立的的取值范围
.
二、选择题：
11.下列各式中,是的二次函数的是 ( )
A．
B．
C． 
D．
12．在同一坐标系中，作
、
、
的图象，它们共同特点是
( )
A． 都是关于轴对称，抛物线开口向上 B．都是关于轴对称，抛物线开口向下
B． 都是关于原点对称，顶点都是原点 D．都是关于轴对称，顶点都是原点
13．抛物线
的图象过原点，则为（ ）
A．0 B．1 C．－1 D．±1
14．把二次函数
配方成为（ ）
A．
B． 
C．
D．
15．已知原点是抛物线
的最高点，则的范围是( )
A． 
B． 
C．
D．
16、函数
的图象经过点( )
A、（－1，1） B、（1 ，1） C、（0 , 1） D 、(1 , 0 )
17、抛物线
向右平移1个单位，再向下平移2个单位，所得到的抛物线是( )
A、
B、
C、
D、
18、已知
关于
的函数关系式
（ 
为正常数，为时间）如图，则函数图象为 ( )
h
h
h
h
o
o
t
t
o
t
o
t
A B C D
19、下列四个函数中, 图象的顶点在y轴上的函数是（ ）
A、
B、
C、
D、
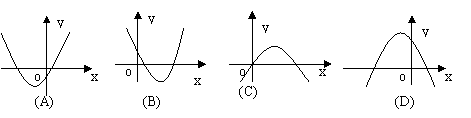20、已知二次函数
，若
，
，那么它的图象大致是（ ）
三、解答题：
21、根据所给条件求抛物线的解析式：
（1）、抛物线过点（0，2）、（1，1）、（3，5）
（2）、抛物线关于轴对称，且过点（1，－2）和（－2，0）
22．已知二次函数
的图像经过A（0，1），B（2，－1）两点.
(1)求
和
的值； (2）试判断点P（－1，2）是否在此函数图像上？
23、某广告公司设计一幅周长为12米的矩形广告牌，广告设计费为每平方米1000元，设矩形一边长为米，面积为S平方米.
（1）
求出S与之间的函数关系式，并确定自变量的取值范围；
（2） 请你设计一个方案，使获得的设计费最多，并求出这个费用.
24、某工厂现有80台机器，每台机器平均每天生产384件产品，现准备增加一批同类机器以提高生产总量，在试生产中发现，由于其他生产条件没变，因此每增加一台机器，每台机器平均每天将少生产4件产品．
（1）如果增加x台机器，每天的生产总量为y件，请你写出y与x之间的关系式；
（2）增加多少台机器，可以使每天的生产总量最大？最大生产总量是多少？
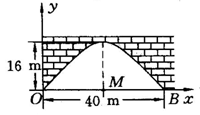
25、如图，有一个抛物线的拱形立交桥，这个桥拱的最大高度为16m，跨度为40m，现把它放在如图所示的直角坐标系里，若要在离跨度中心点M5m处垂直竖一根铁柱支撑这个拱顶，铁柱应取多长？
 |
24、如图，抛物线
经过点A(1，0)，与y轴交于点B.
⑴求抛物线的解析式；
⑵P是y轴正半轴上一点，且△PAB是以AB为腰的等腰三角形，试求P点坐标.
 |
第26章 二次函数单元检测 （B） 姓名___ ____
一、新课标基础训练
1．下列二次函数的图象的开口大小，从大到小排列依次是（ ）
①y=
x2；②y=
x2+3；③y=-
（x-3）2-2；④y=-
x2+5x-1．
A．④②③① B．①③②④ C．④②①③ D．②③①④
2．将二次函数y=3（x+2）2-4的图象向右平移3个单位，再向上平移1个单位，所得的图象的函数关系式（ ）
A．y=3（x+5）2-5； B．y=3（x-1）2-5；C．y=3（x-1）2-3； D．y=3（x+5）2-3
3．将进货单价为70元的某种商品按零售价100元一个售出时，每天能卖出20个，若这种商品的零售价在一定范围内每降价1元，其日销量就增加1个，为了获取最大利润，则应降价（ ）
A．5元 B．10元 C．15元 D．20元
4．若直线y=ax+b（ab≠0）不过第三象限，则抛物线y=ax2+bx的顶点所在的象限是（ ）
A．一 B．二 C．三 D．四
5．已知二次函数y=x2+x+m，当x取任意实数时，都有y>0，则m的取值范围是（ ）
A．m≥
B．m> C．m≤ D．m<
6．二次函数y=mx2-4x+1有最小值-3，则m等于（ ）
A．1 B．-1 C．±1 D．±
二、新课标能力训练
7．如图，用2m长的木条，做一个有横档的矩形窗子，为使透进的
光线最多，那么这个窗子的面积应为_______m2．
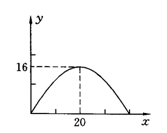8．如图，有一个抛物线型拱桥，其最大高度为16m，
跨度为40m， 现把它的示意图放在平面直角坐标系
中，则此抛物线的函数关系式为__________．
9、已知函数
是关于x的二次函数，
求：(1)满足条件的m值；
(2)m为何值时，抛物线有最低点?求出这个最低点．这时当x为何值时，y随x的增大而增大?
（3）m为何值时，函数有最大值?最大值是什么?这时当x为何值时，y随x的增大而减小?
10、观察表格：
| x | 0 | 1 | 2 |
| ax2 | 1 | ||
| ax2+bx+c | 3 | 3 |
（1）求a，b，c的值，并在表内空格处填入正确的数．
（2）画出函数y=ax2+bx+c的图象，由图象确定，当x取什么实数时，ax2+bx+c>0．
11、如图(2)，已知平行四边形ABCD的周长为8cm，∠B＝30。 若边长AB＝x(cm)。
(1) 
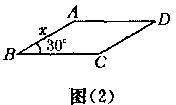求□ABCD的面积y(cm2)与x的函数关系式，并写出自变量x的取值范围。
(2)当x取什么值时，y的值最大?并求最大值。
三、新课标理念中考题
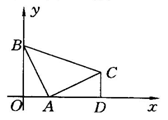12．如图，已知直线y=-2x+2分别与x轴、y轴交于点A、B，以线段AB为直角边在第一象限内作等腰直角三角形ABC，∠BAC=90°，过C作CD⊥x轴，D为垂足．
（1）求点A、B的坐标和AD的长；
（2）求过B、A、C三点的抛物线的解析式．
13、如图，二次函数的图象经过点M（1，—2）、N（—1，6）．
（1）求二次函数的关系式．
（2）把Rt△ABC放在坐标系内，其中∠CAB = 90°，点A、B的坐标分别为（1，0）、（4，0），
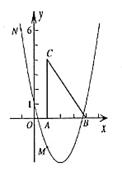BC = 5。将△ABC沿x轴向右平移，当点C落在抛物线上时，求△ABC平移的距离．
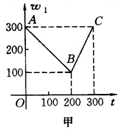
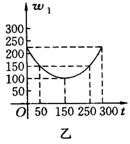
14、黄冈市某蔬菜基地种植西红柿，由历年市场行情得知，从2月1日起的300天内，西红柿市场售价与上市时间的关系用图甲的一条折线表示；西红柿的种植成本与上市时间的关系用图乙表示的抛物线段表示．
（1）写出图甲表示的市场售价与时间的函数关系式；
（2）写出图乙表示的种植成本与时间的函数关系式；
（3）设定市场售价减去种植成本为纯收益，问何时上市的西红柿纯收益最大？
（注：市场售价和种植成本的单位：元/102kg，时间单位：天）
15、已知： ABCD在直角坐标系中的位置如图，O是坐标原点，OB：OC：OA＝1：3：5，
S ABCD＝12，抛物线经过D、A、B三点。
①求A、C两点的坐标；
②求抛物线解析式；
16、已知二次函数y=ax2+bx+c的图象经过点A（2，4），其顶点横坐标为，且(
)2-
=13．
（1）求此二次函数的解析式；
（2）抛物线与x轴交于B，C两点，在x轴上方的上，是否存在点P，使得S△ABC=2S△PBC，如存在，请求出所有满足条件的点P的坐标；如不存在，请说明理由．
