二〇〇七年高中阶段教育数学招生考试试卷
(全卷满分150分,120分钟完卷)
第I卷 选择题(共30分)
注意事项:1.考生姓名、考号、考试科目,应在答题卡上“先填后涂”.
2.每小题选出的答案,必须用2B铅笔在答题卡上“对应涂黑”.
3.答题卡上答案项需改动,应用橡皮擦擦干净后再涂.
一、选择题:每小题给出的四个选项中,只有一项是符合题目要求的,请将正确的选项填入题后的括号内.(本题共10个小题,每小题3分,共30分)
1.下列各式计算正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.2007年我市初中毕业生约为![]() 万人,把
万人,把![]() 万用科学记数表示且保留两个有效数字为( )
万用科学记数表示且保留两个有效数字为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 万
万
3.李明为好友制作一个(图1)正方体礼品盒,六面上各有一字,连起来就是“预祝中考成功”,其中“预”的对面是“中”,“成”的对面是“功”,则它的平面展开图可能是( )
 |
4.下列说法正确的是( )
A.要想了解![]() 各球队在
各球队在![]() 赛季的比赛结果,应采用民意调查法
赛季的比赛结果,应采用民意调查法
B.某工厂质检人员检测灯泡的使用寿命采用普查法
C.要了解某小组各学生某次数学测试成绩采用抽样调查法
 D.了解我市中学生的身体素质状况采用抽样调查法
D.了解我市中学生的身体素质状况采用抽样调查法
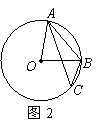
5.如图2,![]() 是
是![]() 的外接圆,已知
的外接圆,已知![]() ,则
,则![]() 的大小为( )
的大小为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.下列说法错误的是( )
A.同时抛两枚普通正方体骰子,点数都是4的概率为![]()
B.不可能事件发生机会为![]()
C.买一张彩票会中奖是可能事件
D.一件事发生机会为![]() ,这件事就有可能发生
,这件事就有可能发生
7.一元二次方程![]() 的根的情况为( )
的根的情况为( )
A.有两个相等的实数根 B.有两个不相等的实数根
C.只有一个实数根 D.没有实数根
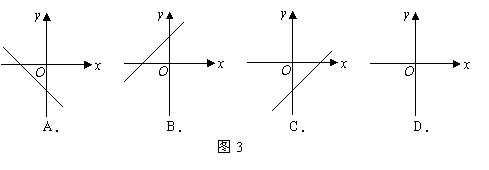 8.函数
8.函数![]() 在直角坐标系中的图象可能是( )
在直角坐标系中的图象可能是( )
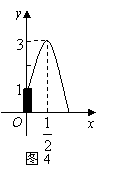 9.巴人广场中心标志性建筑处有高低不同的各种喷泉,其中一支高度为1米的喷水管最大高度为3米,此时喷水水平距离为
9.巴人广场中心标志性建筑处有高低不同的各种喷泉,其中一支高度为1米的喷水管最大高度为3米,此时喷水水平距离为![]() 米,在如图4所示的坐标系中,这支喷泉的函数关系式是( )
米,在如图4所示的坐标系中,这支喷泉的函数关系式是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
10.“五一”黄金周,巴中人民商场“女装部”推出“全部服装八折”,男装部推出“全装八五折”的优惠活动,某顾客在女装部购买了原价![]() 元,男装部购买了原价为
元,男装部购买了原价为![]() 元服装各一套,优惠前需付700元,而他实际付款580元,则可列方程组为( )
元服装各一套,优惠前需付700元,而他实际付款580元,则可列方程组为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
二〇〇七年高中阶段教育招生考试
数学试卷
说明:1.全卷满分为150分,120分钟完卷.
2.本试卷分为第I卷和第II卷,第I卷为选择题,答案涂卡,第II卷为非选择题,考生用蓝、黑墨水钢笔或圆珠笔在试卷上做答
3.考试结束后监考老师将答题卡装入专用袋,不装订第I卷,只装订第II卷.
第II卷 非选择题(共120分)
二、填空题(每小题3分,共30分,把答案直接填写在题中横线上)
11.![]() 的相反数是 ,倒数是 ,平方等于 .
的相反数是 ,倒数是 ,平方等于 .
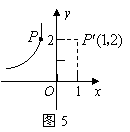 12.函数
12.函数![]() 的自变量
的自变量![]() 的取值范围为 .
的取值范围为 .
13.如图5,点![]() 在双曲线
在双曲线![]() 上,点
上,点![]() 与点
与点![]() 关于
关于![]() 轴对称,则此双曲线的解析式为 .
轴对称,则此双曲线的解析式为 .
14.分解因式:![]() .
.
15.三角形一边长为![]() ,另两边长是方程
,另两边长是方程![]() 的两实根,则这是一个 三角形.
的两实根,则这是一个 三角形.
16.某承陶瓷市场现出售的有边长相等的正三角形、正方形、正五边形的地板砖,某顾客想买其中的两种镶嵌着铺地板,则他可以选择的是 .
17.2007年4月,巴中市出租车收经费方式全面调整,具体收费方式如下,行驶距离在3千米以内(包括3千米)付起步价3元,超过3千米后,每多行驶1千米加收![]() 元,试写出乘车费用
元,试写出乘车费用![]() (元)与乘车距离
(元)与乘车距离![]() (千米)
(千米)![]() 之间的函数关系式为 .
之间的函数关系式为 .
18.某射击运动员五次射击成绩分别为![]() 环,
环,![]() 环,
环,![]() 环,
环,![]() 环,
环,![]() 环,则他这五次成绩的平均数为 ,方差为 .
环,则他这五次成绩的平均数为 ,方差为 .
19.2007年10月1日是中华人民共和国成立58周年纪念日,要在某校选择256名身高基本相同的女同学组成表演方体,在这个问题中我们最值的关注的是该校所有女生身高的 (填“平均数”或“中位数”或“众数”).
20.先阅读下列材料,然后解答问题:
从![]() 三张卡片中选两张,有三种不同选法,抽象成数学问题就是从3个元素中选取2个元素组合,记作
三张卡片中选两张,有三种不同选法,抽象成数学问题就是从3个元素中选取2个元素组合,记作![]() .
.
一般地,从![]() 个元素中选取
个元素中选取![]() 个元素组合,记作:
个元素组合,记作:![]()
例:从7个元素中选5个元素,共有![]() 种不同的选法.
种不同的选法.
问题:从某学习小组10人中选取3人参加活动,不同的选法共有 种.
三、解答题(每小题6分,共18分)
21.计算:![]()
22.计算: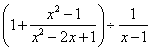
23.解不等式组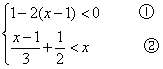
四、解答题(24题9分,25题10分,26题12分,共31分)
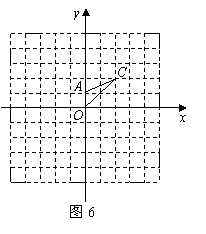 24.如图6,将
24.如图6,将![]() 各顶点的横纵坐标分别乘以
各顶点的横纵坐标分别乘以![]() 作为对应顶点的横纵坐标,得到所得的
作为对应顶点的横纵坐标,得到所得的![]() .
.
①在图中画出所得的![]() (4分)
(4分)
②猜想![]() 与
与![]() 的关系,并说明理由(5分)
的关系,并说明理由(5分)
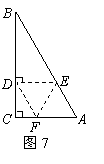 25.如图7,在
25.如图7,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上,把
上,把![]() 沿着
沿着![]() 对折,使点
对折,使点![]() 落在
落在![]() 上点
上点![]() 处,且使
处,且使![]() .
.
(1)猜测![]() 与
与![]() 的数量关系,并说明理由.(5分)
的数量关系,并说明理由.(5分)
(2)求证:四边形![]() 是菱形(5分)
是菱形(5分)
26.巴中市进行课程改革已经五年了,为了了解学生对数学实验教材的喜欢程度,现对某中学初中学生进行了一次问卷调查,具体情况如下:

| 喜欢程序 | 非常喜欢 | 喜欢 | 不喜欢 |
| 人数 |
|
|
①已知该校初一共月480人,求该校初中学生总数.(2分)
②求该校初二学生人数及其扇形的圆心角度数.(3分)
③请补全统计表,并制作条形统计图来反映统计表中的内容.(5分)
④请计算不喜欢此教材的学生的频率,并对不喜欢此教材的同学提出一条建议,希望能通过你的建议让他喜欢上此教材.(2分)
五、(10分)
27.赵明暑假到光雾山旅游,从地理课上知道山区气温会随着海拔高度的增加而下降,沿途他利用随身所带的登山表,测得以下数据:
| 海拔高度 |
|
|
|
|
|
| 气温 |
|
|
|
|
|
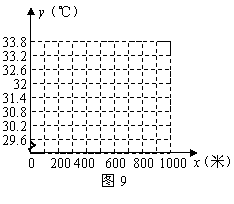
(1)现以海拔高度为![]() 轴,气温为
轴,气温为![]() 轴建立平面直角坐标系(如图9),根据上表中提供的数据描出各点.(3分)
轴建立平面直角坐标系(如图9),根据上表中提供的数据描出各点.(3分)
(2)已知![]() 与
与![]() 之间是一次函数关系,求出这个关系式.(5分)
之间是一次函数关系,求出这个关系式.(5分)
 (3)若赵明到达光雾山山巅时,测得当时气温为
(3)若赵明到达光雾山山巅时,测得当时气温为![]() ,请求出这里的海拔高度.(2分)
,请求出这里的海拔高度.(2分)
六、(10分)
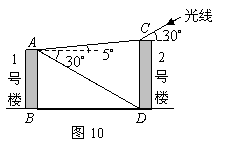 28.如图10所示,某学校拟建两幢平行的教学楼,现设计两楼相距30米,从
28.如图10所示,某学校拟建两幢平行的教学楼,现设计两楼相距30米,从![]() 点看
点看![]() 点,仰角为
点,仰角为![]() ;从
;从![]() 点看
点看![]() 点,俯角为
点,俯角为![]() ,解决下列问题:
,解决下列问题:
(1)求两幢楼分别高多少米?(结果精确到1米)(6分)
(2)若冬日上午![]() 太阳光的入射角最低为
太阳光的入射角最低为![]() (光线与水平线的夹角),问一号楼的光照是否会有影响?请说明理由,若有,则两楼间距离应至少相距多少米时才会消除这种影响?(结果精确到1米)(4分)
(光线与水平线的夹角),问一号楼的光照是否会有影响?请说明理由,若有,则两楼间距离应至少相距多少米时才会消除这种影响?(结果精确到1米)(4分)
(参考数据:![]()
![]()
![]() )
)
七、(10分)
29.在学习勾股定理时,我们学会运用图(I)验证它的正确性;图中大正方形的面积可表示为![]() ,也可表示为
,也可表示为![]() ,即
,即![]() 由此推出勾股定理
由此推出勾股定理![]() ,这种根据图形可以极简单地直观推论或验证数学规律和公式的方法,简称“无字证明”.
,这种根据图形可以极简单地直观推论或验证数学规律和公式的方法,简称“无字证明”.
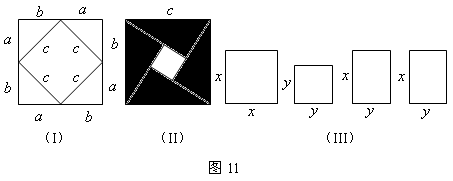
(1)请你用图(II)(2002年国际数字家大会会标)的面积表达式验证勾股定理(其中四个直角三角形全等).(3分)
(2)请你用(III)提供的图形进行组合,用组合图形的面积表达式验证![]() (3分)
(3分)
(3)请你自己设计图形的组合,用其面积表达式验证:
![]() (4分).
(4分).
八、(11分)
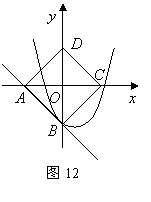 如图12,以边长为
如图12,以边长为![]() 的正方形
的正方形![]() 的对角线所在直线建立平面直角坐标系,抛物线
的对角线所在直线建立平面直角坐标系,抛物线![]() 经过点
经过点![]() 且与直线
且与直线![]() 只有一个公共点.
只有一个公共点.
(1)求直线![]() 的解析式.(3分)
的解析式.(3分)
(2)求抛物线![]() 的解析式.(3分)
的解析式.(3分)
(3)若点![]() 为(2)中抛物线上一点,过点
为(2)中抛物线上一点,过点![]() 作
作![]() 轴于点
轴于点![]() ,问是否存在这样的点
,问是否存在这样的点![]() ,使
,使![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.(5分)
的坐标;若不存在,请说明理由.(5分)