高中、中专、中师招生统一考试数学试卷
(非课改实验区)(黔南)
注意事项:
1.本试卷共8页,26个小题,满分150分,考试时间120分
2.请用蓝黑墨水的钢笔或圆珠笔在试卷上答题,作图用铅笔,可使用不带储存功能的科学计算器
一、填空题(本大题共10小题,每小题3分,满分30分)
1.黔南州人口总数约为,用科学记数法表示为 .
2.不等式![]() 的解集是 .
的解集是 .
3.计算:![]() .
.
4.因式分解:![]() .
.
5.已知点![]() 是函数
是函数![]() 图象上的三点,且
图象上的三点,且![]() ,则
,则![]() 的大小关系是 .
的大小关系是 .
6.当![]() 时,分式
时,分式![]() 的值为零.
的值为零.
7.科学家发现:植物的花瓣,萼片,果实的数目以及其它方面的特征,都非常吻合一个奇待的数列——著名的斐波那契数列:1,1,2,3,5,8,13,21,34,55,……,仔细观察以上数列,则它的第11个数应该是 .
 8.如图1,
8.如图1,![]() 分别是
分别是![]() 的边
的边![]() 上的点,请你添加一个条件,使
上的点,请你添加一个条件,使![]() 与
与![]() 相似,你添加的条件是 .
相似,你添加的条件是 .
9.若将二次函数![]() ,配方成为
,配方成为![]() 的形式(其中
的形式(其中![]() 为常数),则
为常数),则![]() .
.
10.如图2,围棋盘放置在某个平面直角坐标系内,白棋②的坐标为![]() ,白棋④的坐标为
,白棋④的坐标为![]() ,那么黑棋的坐标应该是 .
,那么黑棋的坐标应该是 .
二、单项选择题(每小题4分,共6小题,满分24分)
11.现规定一种运算:![]() ,其中
,其中![]() 为实数,则
为实数,则![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.下列图形中,面积最大的是( )
A.边长为5的正方形
B.半径为![]() 的圆
的圆
C.边长为6,8,10的三角形 D.对角线长为6和8的菱形
13.如果代数式![]() 的值为18,那么代数式
的值为18,那么代数式![]() 的值等于( )
的值等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 14.向一空容器内均匀注水,最后把容器注满,在注水过程中,容器的水面高度与时间的关系如图3所示,图中
14.向一空容器内均匀注水,最后把容器注满,在注水过程中,容器的水面高度与时间的关系如图3所示,图中![]() 为线段,则这个容器是( )
为线段,则这个容器是( )
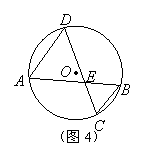 15.如图4,
15.如图4,![]() 的弦
的弦![]() 相交于
相交于![]() ,已知
,已知![]() ,
,![]() ,那么
,那么![]() 的度数是( )
的度数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
16.秋千拉绳长3米,静止时踩板离地面0.5米,某小朋友荡秋千时,秋千在最高处踩板离地面2米(左右对称),如图5所示,则该秋千所荡过的圆弧长为( )
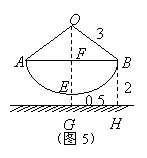 A.
A.![]() 米 B.
米 B.![]() 米 C.
米 C.![]() 米 D.
米 D.![]() 米
米
三、解答题(本大题共10小题,满分96分)
17.(本题满分10分,(1)小题5分,(2)小题5分)
(1)计算:![]()
(2)用换元法解方程:![]() .
.
18.(本题满分6分)
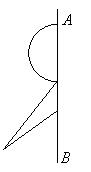 如图,是由半圆和三角形组成的图形,请以
如图,是由半圆和三角形组成的图形,请以![]() 为对称轴,作出图形的另一半(用尺规作图,只保留作图痕迹,不写作法和证明)
为对称轴,作出图形的另一半(用尺规作图,只保留作图痕迹,不写作法和证明)
19.(本题满分10分)
 如图,梯形
如图,梯形![]() 中,
中,![]() ,
,![]() ,
,![]() 为梯形
为梯形![]() 外一点,
外一点,![]() 分别交线段
分别交线段![]() 于点
于点![]() ,且
,且![]() .
.
(1)写出图中三对你认为全等的三角形(不再添加辅助线)
(2)选择你在(1)中写出全等三角形中任意一对进行证明.
20.(本题满分7分)阅读材料题:
在平面直角坐标系中,已知![]() 轴上两点
轴上两点![]() ,
,![]() 的距离记作
的距离记作![]() ,如
,如![]() ,
,![]() 是平面上任意两点,我们可以通过构造直角三角形来求
是平面上任意两点,我们可以通过构造直角三角形来求![]() 间距离,如图,过
间距离,如图,过![]() 分别向
分别向![]() 轴,
轴,![]() 轴作垂线,
轴作垂线,![]() 和
和![]() ,垂足分别是
,垂足分别是![]() ,
,![]() ,
, ![]() ,
,![]() ,直线
,直线![]() 交
交![]() 于
于![]() ,在
,在![]() 中,
中,![]() .
.
![]() ,
,![]()
![]() .
.
由此得任意两点![]() 间距离公式
间距离公式![]()
(1)直接应用平面内两点间距离公式,求点![]() 之间的距离;
之间的距离;
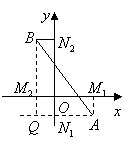 (2)若
(2)若![]() 是平面上一定点,
是平面上一定点,![]() 是平面上一动点,且
是平面上一动点,且![]() 间的距离恒为2,运用平面内两点间距离公式,写出关于
间的距离恒为2,运用平面内两点间距离公式,写出关于![]() 满足的方程,并说出此方程的图像是什么?
满足的方程,并说出此方程的图像是什么?
21.(本题满分10分)
已知:三角形![]() 内接于
内接于![]() ,过
,过![]() 作直线
作直线![]()
(1)如图,![]() 为直径,要使得
为直径,要使得![]() 是
是![]() 的切线,还需添加的条件是(只需写出三种情况)
的切线,还需添加的条件是(只需写出三种情况)
①_______________②_______________③_______________
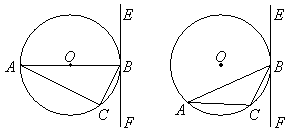 (2)如图,
(2)如图,![]() 为非直径的弦,已知
为非直径的弦,已知![]()
求证:![]() 是
是![]() 的切线
的切线
22.(本题满分10分)
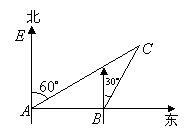 某船以每小时
某船以每小时![]() 海里的速度向正东方向航行,在点
海里的速度向正东方向航行,在点![]() 测得某岛
测得某岛![]() 在北偏东
在北偏东![]() 方向上,航行半小时后到达点
方向上,航行半小时后到达点![]() ,测得该岛在北偏东
,测得该岛在北偏东![]() 方向上,已知该岛周围
方向上,已知该岛周围![]() 海里内有暗礁
海里内有暗礁
(1)试说明点![]() 是否在暗礁区域外?
是否在暗礁区域外?
(2)若继续向东航行有无触礁危险?请说明理由.
23.(本题满分11分)
一农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出土豆千克数与他手中持有的钱数(含备用零钱)的关系如图所示,结合图像解答下列问题.
(1)农民自带的零钱是多少?
(2)降价前他每千克土豆出售价格是多少?
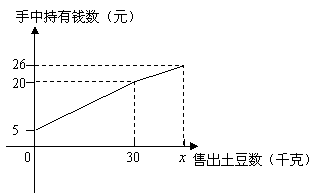 (3)降价后他按每千克
(3)降价后他按每千克![]() 元将剩余土豆售完,这时他手中的钱(含备用零钱)是
元将剩余土豆售完,这时他手中的钱(含备用零钱)是![]() 元,问他一共带了多少千克土豆.
元,问他一共带了多少千克土豆.
24.(本题满分10分)
如图,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 从
从![]() 点开始,沿
点开始,沿![]() 边向
边向![]() 运动,速度为
运动,速度为![]() 厘米/秒,点
厘米/秒,点![]() 从点
从点![]() 开始沿
开始沿![]() 边向点
边向点![]() 运动,速度为
运动,速度为![]() 厘米/秒,设四边形
厘米/秒,设四边形![]() 的面积为
的面积为![]() .
.
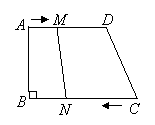 (1)写出面积
(1)写出面积![]() 与时间
与时间![]() 之间的函数关系式;
之间的函数关系式;
(2)当![]() 为何值时,四边形
为何值时,四边形![]() 是平行四边形?
是平行四边形?
(3)当![]() 为何值时,四边形
为何值时,四边形![]() 是等腰梯形?
是等腰梯形?
25.(本题满分10分)
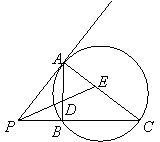 如图,
如图,![]() 为圆的切线,
为圆的切线,![]() 为切点,
为切点,![]() 为割线,
为割线,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
求证:(1)![]() ;(2)
;(2)![]() .
.
26.(本题满分12分)一座隧道的截面由抛物线和长方形构成,长方形的长为![]() ,宽为
,宽为![]() ,隧道最高点
,隧道最高点![]() 位于
位于![]() 的中央且距地面
的中央且距地面![]() ,建立如图所示的坐标系
,建立如图所示的坐标系
(1)求抛物线的解析式;
(2)一辆货车高![]() ,宽
,宽![]() ,能否从该隧道内通过,为什么?
,能否从该隧道内通过,为什么?
 (3)如果隧道内设双行道,那么这辆货车是否可以顺利通过,为什么?
(3)如果隧道内设双行道,那么这辆货车是否可以顺利通过,为什么?
高中、中专、中师招生统一考试
数学试卷(非课改实验区)参考答案
一、1.![]() 2.
2.![]() 3.
3.![]() 4.
4.![]() 5.
5.![]()
6.![]() 7.
7.![]() 8.
8.![]() 或
或![]() 或
或![]()
9.![]() 10.
10.![]()
二、
| 题号 | 11 | 12 | 13 | 14 | 15 | 16 |
| 答案 | C | B | C | C | C | B |
三、17.(1)原式![]() ······ 4分(计算每1项正确给1分,如计算
······ 4分(计算每1项正确给1分,如计算![]() (给1分))
(给1分))
![]() ············································································· 5分
············································································· 5分
(2)![]()
设![]() ················································································· 1分
················································································· 1分
则原方程化为![]()
解得![]() ···································································· 2分
···································································· 2分
当![]() 时,解得
时,解得![]() ································· 3分
································· 3分
当![]() 时,
时,![]()
即![]()
![]()
![]() 方程无解 ······································ 4分
方程无解 ······································ 4分
![]() 原方程的根为
原方程的根为![]() ··································· 5分
··································· 5分
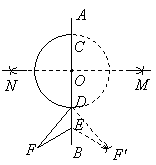 18.(1)分别以
18.(1)分别以![]() 为端点,大于
为端点,大于![]() 作弧,两弧交于
作弧,两弧交于![]() (1分)
(1分)
(2)作直线![]() ,交
,交![]() 于
于![]() (给1分)
(给1分)
(3)以![]() 为半径作已知半圆的另一半(给1分)
为半径作已知半圆的另一半(给1分)
(4)以![]() 点为圆心,
点为圆心,![]() 为半径作弧,然后以
为半径作弧,然后以![]() 点为圆心
点为圆心![]() 为半径作弧,两弧交于点
为半径作弧,两弧交于点![]() (给2分)
(给2分)
(5)连结![]() 和
和![]() (给1分)
(给1分)
19.(1)![]() ,
,![]() (每写对一对给1分,满分3分)
(每写对一对给1分,满分3分)
(2)假设是![]()
证明:![]()
![]() 点在线段
点在线段![]() 的中垂线上 ·············································· 2分
的中垂线上 ·············································· 2分
又![]() 为等腰梯形,
为等腰梯形,![]() 分别为上下底,由对称性可知
分别为上下底,由对称性可知![]() 点也是在
点也是在![]() 的中垂线上 4分
的中垂线上 4分
![]() ········································································· 5分
········································································· 5分
![]() ···························································· 7分(其它证法该相应步骤给分)
···························································· 7分(其它证法该相应步骤给分)
20.(1)解:利用![]()
把![]() 代入上式
代入上式
![]() ················································· 3分
················································· 3分
(2)据题意有:![]() ·········································· 4分
·········································· 4分
则:![]() ························································ 5分
························································ 5分
根据圆的定义可知该图象是一个圆 ············································· 7分
21.(1)①![]() ②
②![]() ③
③![]() ④
④![]()
⑤![]() 以上答案均可选择,与序号无关(只要写对一个给1分,满分3分)
以上答案均可选择,与序号无关(只要写对一个给1分,满分3分)
(2)证明:连结![]() 并延长
并延长![]() 交
交![]() 于
于![]() ,连结
,连结![]() ····················· 1分
····················· 1分
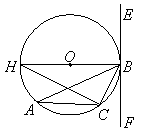
![]() ,
,![]() ····························· 2分
····························· 2分
又![]() 是直径,
是直径,![]() ···················· 3分
···················· 3分
![]() ····································· 4分
····································· 4分
又![]()
![]() ···························································· 5分
···························································· 5分
![]() ················································································· 6分
················································································· 6分
又![]() 是半径,
是半径,![]() 是
是![]() 的切线 ·········································· 7分
的切线 ·········································· 7分
22.(1)过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ········································ 1分
········································ 1分
![]() (海里) ···················································· 2分
(海里) ···················································· 2分
![]()
![]() ··········································································· 3分
··········································································· 3分
又![]() ······················································ 4分
······················································ 4分
即![]()
![]() 点
点![]() 在暗礁区域外 ··································································· 5分
在暗礁区域外 ··································································· 5分
(2)过点![]() 作
作![]() ,垂足为
,垂足为![]() ················································· 6分
················································· 6分
在![]() 中,
中,![]()
令![]() ,则
,则![]() ························································· 7分
························································· 7分
在![]() 中,
中,![]()
![]() ······························· 8分
······························· 8分
![]() ,
,![]()
解得![]() ··················································································· 9分
··················································································· 9分
![]()
![]() 船继续向东航行有触礁的危险 ························· 10分(其它解法相应给分)
船继续向东航行有触礁的危险 ························· 10分(其它解法相应给分)
23.(1)农民自带的零钱为![]() 元 ······························································· 2分
元 ······························································· 2分
(2)设降价每千克售价的价格为![]() 元,据题意 ·································· 3分
元,据题意 ·································· 3分
![]() 元/千克 ························································ 6分
元/千克 ························································ 6分
(3)设他一共带了![]() 斤土豆,根据题意 ············································· 7分
斤土豆,根据题意 ············································· 7分
![]() ······································································ 10分
······································································ 10分
解得![]() (千克)
(千克)
答:他一共带了![]() 千克的土豆. ·············································· 11分
千克的土豆. ·············································· 11分
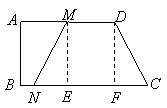
24.(1)根据题意![]()
又![]() ··················································· 1分
··················································· 1分
![]() ····················································································· 2分
····················································································· 2分
而![]()
![]()
![]() ······················································· 3分
······················································· 3分
(2)假设当![]() 时,四边形
时,四边形![]() 为平行四边形,根据平行四边形的判定定理有
为平行四边形,根据平行四边形的判定定理有![]() 5分
5分
即:![]()
解得![]() ··················································································· 6分
··················································································· 6分
![]() 当
当![]() 秒时,四边形为平行四边形.
秒时,四边形为平行四边形.
(3)假设当![]() 时,四边形
时,四边形![]() 是等腰梯形,则
是等腰梯形,则![]() (如右下图)
(如右下图)
···················································· 7分
又作![]() 分别垂直于
分别垂直于![]() ,则
,则
![]()
![]() ················································································ 8分
················································································ 8分
![]() ··················································································· 9分
··················································································· 9分
![]() ,解得
,解得![]() (秒). ·································· 10分
(秒). ·································· 10分
25.证法一:(1)![]() 平分
平分![]() ,
,![]() ···················· 1分
···················· 1分
![]() 为圆的切线,
为圆的切线,![]() . ··············· 2分
. ··············· 2分
![]() ,
,
![]() , ······························· 3分
, ······························· 3分
![]() . ·········································· 4分
. ·········································· 4分
(2)![]() ,且
,且![]() ,
,
![]() , ········································· 5分
, ········································· 5分
![]() . ················································································ 7分
. ················································································ 7分
![]() ,且
,且![]() ,
,
![]() , ······································································ 8分
, ······································································ 8分
![]() . ················································································ 9分
. ················································································ 9分
![]() ,
,![]() . ··········································· 10分
. ··········································· 10分
证法二:(1)同上
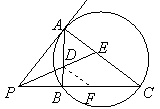 (2)过点
(2)过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,
,
![]() ,
,![]() .
.
![]() ,且
,且![]() .
.
又![]() ,
,
![]() .
.
由(1)知:![]() ,
,
![]() ,
,![]() .(按相应的给分)
.(按相应的给分)
26.(1)由题意可知抛物线经过点![]() ················ 2分
················ 2分
设抛物线的方程为![]() ············································· 3分
············································· 3分
将![]() 三点的坐标代入抛物线方程.
三点的坐标代入抛物线方程.
解得抛物线方程为![]() ········································· 5分(解出
········································· 5分(解出![]() 的值可分别给1分)
的值可分别给1分)
(2)令![]() ,则有
,则有![]() ··········································· 6分
··········································· 6分
解得![]() ················································ 7分
················································ 7分
![]() ····································································· 8分
····································································· 8分
![]() 货车可以通过. ······································································· 9分
货车可以通过. ······································································· 9分
(3)由(2)可知![]() ············································· 11分
············································· 11分
![]() 货车可以通过. ····································································· 12分
货车可以通过. ····································································· 12分