高中阶段学校招生考试数学试卷课改实验区
说明:全卷共8页,考试时间90分,满分150分.
一、选择题(每小题3分,共36分,每小题给出4个答案,其中只有一个正确,把所选答案的编号写在题目后面的括号内)
1.![]() 的相反数是( )
的相反数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.今年我市参加中考的人数约是![]() ,数据
,数据![]() 用科学记数法表示为( )
用科学记数法表示为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.在下列长度的四根木棒中,能与3cm,7cm两根木棒围成一个三角形的是( )
A.7cm B.4cm C.3cm D.10cm
4.下列运算正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.点![]() 关于
关于![]() 轴对称的点的坐标是( )
轴对称的点的坐标是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.下图中所示的几何体的主视图是( )
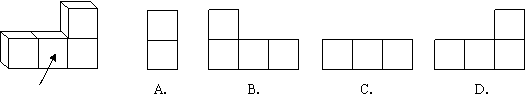 |
7.下列事件是必然事件的是( )
A.今年10月1日湛江的天气一定是晴天
B.2008年奥运会刘翔一定能夺得110米跨栏冠军
C.当室外温度低于![]() ℃时,将一碗清水放在室外会结冰
℃时,将一碗清水放在室外会结冰
D.打开电视,正在播广告
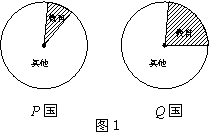 8.图1是
8.图1是![]() 两国2005年财政经费支出情况的扇形统计图.根据统计图,下面对两国全年教育经费支出判断正确的是( )
两国2005年财政经费支出情况的扇形统计图.根据统计图,下面对两国全年教育经费支出判断正确的是( )
A.![]() 国比
国比![]() 国多
国多
B.![]() 国比
国比![]() 国多
国多
C.![]() 国与
国与![]() 国一样多
国一样多
D.无法确定哪国多
9.数据12,10,13,8,17,10,21的中位数是( )
A.8 B.10 C.13 D.12
10.在一个不透明的口袋中,有大小、形状完全相同,颜色不同的球15个,从中摸出红球的概率为![]() ,则袋中红球的个数为( )
,则袋中红球的个数为( )
A.10 B.15 C.5 D.3
11.小颖从家出发,直走了20分钟,到一个离家1000米的图书室,看了40分钟的书后,用15分钟返回到家,下图中表示小颖离家时间与距离之间的关系的是( )
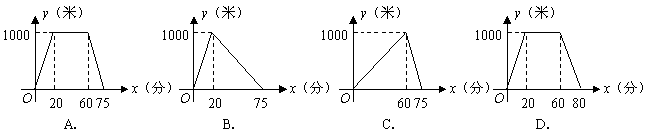
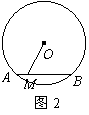 12.如图2,
12.如图2,![]() 的半径为5,弦
的半径为5,弦![]() 的长为8,点
的长为8,点![]() 在线段
在线段![]() (包括端点
(包括端点![]() )上移动,则
)上移动,则![]() 的取值范围是( )
的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
二、填空题(每小题3分,共24分,请把答案填在横线上)
13.分解因式:![]() .
.
14.请写出一个图象位于第二、四象限的反比例函数: .
15.数据100,99,99,100,102,100的方差![]() .
.
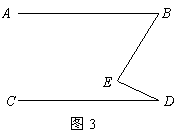
16.如图3,已知直线![]() ,
,![]() ,
,![]() ,则
,则![]() 度.
度.
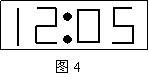
17.图4是平面镜里看到背向墙壁的电子钟示数,这时的实际时间应该是 .
 | |||
 | |||
18.下面是一个简单的数值运算程序,当输入![]() 的值为2时,输出的数值是 .
的值为2时,输出的数值是 .
19.如果一个扇形的圆心角为![]() ,半径为
,半径为![]() ,那么该扇形的弧长是 .
,那么该扇形的弧长是 .
20.观察下列顺序排列的等式:![]() ,….试猜想第
,….试猜想第![]() 个等式(
个等式(![]() 为正整数):
为正整数):![]() .
.
三、解答题(每小题6分,共30分)
21.计算:![]() .
.
22.先化简,再求值:![]() ,其中
,其中![]() .
.
23.如图5,请你画出方格纸中的图形关于点![]() 的中心对称图形,并写出整个图形的对称轴的条数.
的中心对称图形,并写出整个图形的对称轴的条数.
 |
24.近年来,我市开展以“四通五改六进村”为载体,以生态文明为主要特色的新农村建设活动取得了明显成效.下面是市委领导和市民的一段对话,请你根据对话内容,替市领导回答市民提出的问题(结果精确到0.1%).
 |


领导

市民
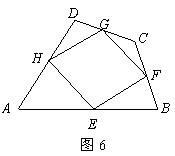
25.如图6,点![]() 分别为四边形
分别为四边形![]() 的边
的边![]() 的中点,试判断四边形
的中点,试判断四边形![]() 的形状,并证明你的结论.
的形状,并证明你的结论.
 |
四、解答题(每小题9分,共36分)
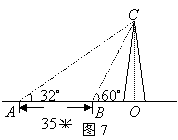
26.小刘同学为了测量雷州市三元塔的高度,如图7,她先在![]() 处测得塔顶
处测得塔顶![]() 的仰角为
的仰角为![]() ,再向塔的方向直行35米到达
,再向塔的方向直行35米到达![]() 处,又测得塔顶
处,又测得塔顶![]() 的仰角为
的仰角为![]() ,请你帮助小刘计算出三元塔的高度(小刘的身高忽略不计,结果精确到1米).
,请你帮助小刘计算出三元塔的高度(小刘的身高忽略不计,结果精确到1米).
 |
27.为了让学生了解安全知识,增强安全意识,我市某中学举行了一次“安全知识竞赛”.为了了解这次竞赛成绩情况,从中抽取了部分学生的成绩(得分取整数,满分为100分)为样本,绘制成绩统计图,如图8所示,请结合统计图回答下列问题:
(1)本次测试的样本容量是多少?
(2)分数在80.5~90.5这一组的频率是多少?
(3)若这次测试成绩80分以上(含80分)为优秀,则优秀人数不少于多少人?
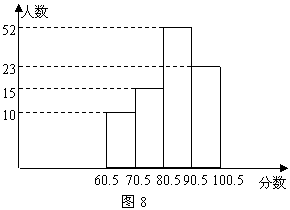 |
28.某工厂现有甲种原料280kg,乙种原料190kg,计划用这两种原料生产![]() 两种产品50件,已知生产一件
两种产品50件,已知生产一件![]() 产品需甲种原料7kg、乙种原料3kg,可获利400元;生产一件
产品需甲种原料7kg、乙种原料3kg,可获利400元;生产一件![]() 产品需甲种原料3kg,乙种原料 5kg,可获利350元.
产品需甲种原料3kg,乙种原料 5kg,可获利350元.
(1)请问工厂有哪几种生产方案?
(2)选择哪种方案可获利最大,最大利润是多少?
29.如图9,![]() 是
是![]() 的直径,
的直径,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作直线
作直线![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
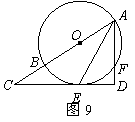 (2)若
(2)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
五、解答题(每小题12分,共24分)
30.如图10,在![]() 中,
中,![]() ,
,![]() ,把边长分别为
,把边长分别为![]() 的
的![]() 个正方形依次放入
个正方形依次放入![]() 中,请回答下列问题:
中,请回答下列问题:
(1)按要求填表
|
| 1 | 2 | 3 |
|
|
(2)第![]() 个正方形的边长
个正方形的边长![]() ;
;
(3)若![]() 是正整数,且
是正整数,且![]() ,试判断
,试判断![]() 的关系.
的关系.
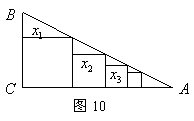 |
31.已知抛物线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,
,![]()
![]() ,且
,且![]() 是方程
是方程![]() 的两个实数根,点
的两个实数根,点![]() 为抛物线与
为抛物线与![]() 轴的交点.
轴的交点.
(1)求![]() 的值;
的值;
(2)分别求出直线![]() 和
和![]() 的解析式;
的解析式;
(3)若动直线![]() 与线段
与线段![]() 分别相交于
分别相交于![]() 两点,则在
两点,则在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 为等腰直角三角形?若存在,求出点
为等腰直角三角形?若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
 |
高中阶段学校招生考试数学试题课改实验区
参考答案及评分标准
一、选择题(每小题3分,共36分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | C | A | B | D | D | C | D | D | C | A | A |
二、填空题(每小题3分,共24分)
13.![]() 14.
14.![]() 等 15.1 16.80 17.
等 15.1 16.80 17.![]()
18.1 19.![]() 20.
20.![]()
三、解答题(每小题6分,共30分)
21.解:原式![]() ··························································································· 4分
··························································································· 4分
![]() .······································································································ 6分
.······································································································ 6分
22.解:原式![]() ························································································· 2分
························································································· 2分
![]() ······························································································ 3分
······························································································ 3分
![]() ··································································································· 4分
··································································································· 4分
当![]() 时,原式
时,原式![]() ························································································ 5分
························································································ 5分
![]() ························································································· 6分
························································································· 6分
23.解:如图1,·········································································································· 4分
共有4条对称轴.········································································································· 6分
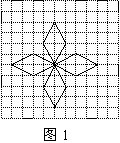 |
24.解:设平均每年生态文明村增长率是![]() ,根据题意,得·········································· 1分
,根据题意,得·········································· 1分
![]() ····················································································· 3分
····················································································· 3分
解得:![]() (不合题意,舍去)·················································· 5分
(不合题意,舍去)·················································· 5分
答:平均每年生态文明村增长率约是18.1%.································································ 6分
25.解:四边形![]() 是平行四边形··········································································· 1分
是平行四边形··········································································· 1分
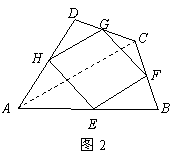 证明:连结
证明:连结![]() ,如图2.
,如图2.
![]() 分别是
分别是![]() 的中点,
的中点,
![]() 是
是![]() 的中位线,……………………2分
的中位线,……………………2分
![]() ,且
,且![]() .………………3分
.………………3分
同理:![]() ,且
,且![]() ,…………4分
,…………4分
![]() .……………………………………5分
.……………………………………5分
![]() 四边形
四边形![]() 是平行四边形.·················································································· 6分
是平行四边形.·················································································· 6分
26.解:在![]() 中,
中,
![]() .············································································································ 2分
.············································································································ 2分
在![]() 中,
中,
![]() .············································································································ 4分
.············································································································ 4分
![]() ,
,
![]() ,··························································································· 6分
,··························································································· 6分
 (米)········································································ 8分
(米)········································································ 8分
答:三元塔的高度约是34米.······················································································ 9分
27.解:(1)![]() ,
,
![]() 本次测试的样本容量是100.····················································································· 3分
本次测试的样本容量是100.····················································································· 3分
(2)![]() .
.
![]() 分数在80.5~90.5这一组的频率是0.52.···································································· 6分
分数在80.5~90.5这一组的频率是0.52.···································································· 6分
(3)![]() ,
,
![]() 优秀人数不少于75人.····························································································· 9分
优秀人数不少于75人.····························································································· 9分
28.解:(1)设生产![]() 产品
产品![]() 件,生产
件,生产![]() 产品
产品![]() 件,则······································· 1分
件,则······································· 1分
![]() ································································································· 2分
································································································· 2分
解得:![]() .······························································································· 3分
.······························································································· 3分
![]() 为正整数,
为正整数,![]()
![]() 可取30,31,32.
可取30,31,32.
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,·························································································· 4分
,·························································································· 4分
所以工厂可有三种生产方案,分别为:
方案一:生产![]() 产品30件,生产
产品30件,生产![]() 产品20件;
产品20件;
方案二:生产![]() 产品31件,生产
产品31件,生产![]() 产品19件;
产品19件;
方案三:生产![]() 产品32件,生产
产品32件,生产![]() 产品18件;··························································· 5分
产品18件;··························································· 5分
(2)方案一的利润为:![]() 元;
元;
方案二的利润为:![]() 元;
元;
方案三的利润为:![]() 元.······················································ 8分
元.······················································ 8分
因此选择方案三可获利最多,最大利润为19100元.····················································· 9分
29.(1)证明:连结![]() ,如图3.
,如图3.
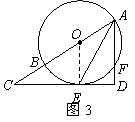
![]() 平分
平分![]() ,
,
![]() .……………………1分
.……………………1分
![]() ,
,
![]() ,……………………2分
,……………………2分
![]() ,
,
![]() .……………………………3分
.……………………………3分
![]() ,
,
![]() ,
,
![]() 是
是![]() 的切线.·································································································· 4分
的切线.·································································································· 4分
(2)设![]() 是
是![]() 的半径,
的半径,
在![]() 中,
中,![]() ············································································ 5分
············································································ 5分
即![]() .
.
解得![]() .·················································································································· 6分
.·················································································································· 6分
![]() ,
,
![]() ,
,
![]() .·································································································· 7分
.·································································································· 7分
即![]() .
.
解得![]() .·························································································· 8分
.·························································································· 8分
![]()
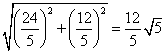 .························································································ 9分
.························································································ 9分
30.(1)![]() ········································································································ 6分
········································································································ 6分
(2)![]() .················································································································ 8分
.················································································································ 8分
(3)![]()
![]() ······················································································· 10分
······················································································· 10分
![]() .································································································· 11分
.································································································· 11分
![]() .······································································································· 12分
.······································································································· 12分
31.解:(1)由![]() ,得
,得![]() .
.
![]() ,··································································································· 1分
,··································································································· 1分
把![]() 两点的坐标分别代入
两点的坐标分别代入![]() 联立求解,得
联立求解,得
![]() .······································································································ 2分
.······································································································ 2分
(2)由(1)可得![]() ,
,![]() 当
当![]() 时,
时,![]() ,
,![]() .
.
设![]() ,把
,把![]() 两点坐标分别代入
两点坐标分别代入![]() ,联立求得
,联立求得
![]() .
.![]() 直线
直线![]() 的解析式为
的解析式为![]() .····················································· 3分
.····················································· 3分
同理可求得直线![]() 的解析式是
的解析式是![]() .···························································· 4分
.···························································· 4分
(3)假设存在满足条件的点![]() ,并设直线
,并设直线![]() 与
与![]() 轴的交点为
轴的交点为![]() .
.
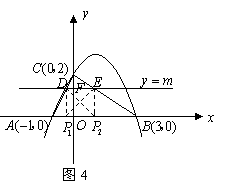 ①当
①当![]() 为腰时,分别过点
为腰时,分别过点![]() 作
作![]() 轴于
轴于![]() ,作
,作![]() 轴于
轴于![]() ,如图4,则
,如图4,则![]() 和
和![]() 都是等腰直角三角形,
都是等腰直角三角形,
![]() ,
,
![]() .
.
![]() ,
,![]() ,
,
![]() ,即
,即![]() .
.
解得![]() .················································································································ 6分
.················································································································ 6分
![]() 点
点![]() 的纵坐标是
的纵坐标是![]() ,
,![]() 点
点![]() 在直线
在直线![]() 上,
上,
![]() ,解得
,解得![]() ,
,![]() .
.
![]()
![]() ,同理可求
,同理可求![]() .··············································································· 8分
.··············································································· 8分
②当![]() 为底边时,
为底边时,
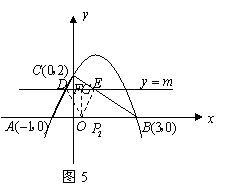 过
过![]() 的中点
的中点![]() 作
作![]() 轴于点
轴于点![]() ,如图5,
,如图5,
则![]() ,
,
由![]() ,
,
得![]() ,即
,即![]() ,
,
解得![]() .…………………………………………9分
.…………………………………………9分
同1方法.求得![]() ,
,
![]()
![]() ,
,![]() .····························································· 11分
.····························································· 11分
结合图形可知,![]() ,
,
![]() ,
,
![]() 是
是![]() ,
,![]() 也满足条件.
也满足条件.
综上所述,满足条件的点![]() 共有3个,即
共有3个,即![]() .················ 12分
.················ 12分
说明:以上各题如有其他解(证)法,请酌情给分.