初三数学期中试卷2
一、填空题（每空2分，共40分）
1、
=__________，
__________；
2、
， ， 
；
3、某汽车上山的速度是
千米/时，原路下山的速度是
千米/时，则该汽车上下山的平均速度是__________千米/时。
4、当
__________时，分式
无意义，当__________时，分式
有意义，当__________时，分式
的值为零；
5、方程
化成一元二次方程的一般形式为_______，其中二次项系数，一次项系数，常数项分别为________；
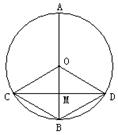
6、如图，AB是⊙O的直径，弦CD⊥AB于M，∠COD=120°，⊙O的半径为6，则CD=__________，四边形OCBD是怎样的特殊四边形__________（选填平行四边形、矩形、菱形、正方形）；
7、Rt△ABC中，AB=4，AC=3，∠A=90°，以A为圆心，R为半径作圆，当R=_________时，⊙A与BC相切。当R满足__________条件时，点C在⊙A内，但点B在⊙A外；
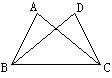8、已知AB是⊙O的直径，且AB=12，C、D在⊙O上，且∠BAC=60°,∠BAD=30°，则∠ACD=__________，CD=__________；
9、如图，当__________________或___________________时，
△ABC≌△DCB（一条横线上只能补充两个条件）。
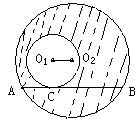10、如图⊙O1与⊙O2的弦AB切于点C，且O1O2∥AB，若AB=8，则阴影部分的面积为__________，若⊙O1的半径为2，⊙O2的半径为4，则扇形O2AB的周长为__________。
二、选择题（每题3分，共24分）
11、下列变形正确的是………………………………………………………………（ ）
A、
B、
C、
D、
12、将分式
用含
的代数式表示，则得……………………………（ ）
A、
B、
C、
D、
13、若关于的一元二次方程
的根的判别式△=4，则这个方程的两个根为………………………………………………………………………………………（ ）
A、2，2 B、5，－1 C、1，3 D、－1，－3
14、若一个一元二次方程的根分别是
各根的平方，则这个方程是………………………………………………………………………………………（ ）
A、
B、
C、
D、
15、在⊙O中，如果⌒ AB=2⌒ CD，那么弦AB与2CD的大小关系是……………（ ）
A、AB=2CD B、AB＞2CD C、AB＜2CD D、不能确定
16、从圆外一点作圆的两条切线，如果两切线的夹角为60°，两切点间的距离为，那么圆的半径为…………………………………………………………………………（ ）
A、
B、
C、
D、
17、在长度分别是3，4，8的三条线段中，任取两条线段作两圆的半径，第三条线段作圆心距，则两圆的位置关系是………………………………………………………（ ）
A、外离或相交 B、内含或相交 C、外离或内含 D、外离或内含或相交
18、△ABC中，AB=4，AC=6，M为BC边上的中点，则AM的长度取值范围是………………………………………………………………………………………（ ）
A、1＜AM＜5 B、2＜AM＜10 C、4＜AM＜6 D、6＜AM＜10
三、解答题
19、解方程
（4分）
20、解方程
（4分）
21、解方程
（4分）
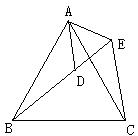22、已知：如图△ABC和△ADE都是等边三角形，图中哪个三角形与△ABD全等？证明你的结论。（4分）
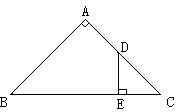23、如图Rt△ABC中，∠A=90°，AB=AC，D是∠B的平分线与AC的交点，DE⊥BC于E。请猜想△DEC的周长与BC的关系？并证明你的猜想。（4分）
24、已知：如图，两个等圆⊙O1和⊙O2相交于A、B两点，过A作⊙O1的直径AC，与⊙O2交于点D，E为DC中点，
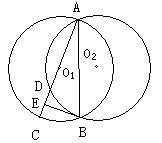⑴求证：AC⊥BE；⑵若两圆的半径都是5㎝，且AD∶DC=3∶2，求AB的长。（6分）
25、已知关于的方程
，⑴当
为何值时，此方程有实数根；⑵若此时方程的两实数根为
，
，满足：
，求的值。（6分）
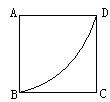
26、某个体生产厂想利用边长为8㎝的正方形做一批工艺品，设计方案如下：以A为圆心，8㎝长为半径裁扇形ABD，把扇形ABD卷成一个圆锥，正方形余下的部分裁出一个圆，问这个圆能否做上述卷成圆锥的底？若能，请计算出这个圆锥工艺品的高。若不能，请说明为什么？并帮这个生产厂提出一个改进的设计方案。（8分）
 |
27、小明为书房买灯，现有两种灯可供选购，其中一种是9W（即0.009KW）的节能灯，售价为49元/盏；另一种是40W的白炽灯，售价为18元/盏。假设两种灯的照明亮度一样，使用寿命都可以达到2800小时，已知小明家所在地的电价为每KW0.5元。
⑴设照明时间为小时，请用含的代数式分别表示一盏节能灯和一盏白炽灯的费用。
⑵小明想在这两种灯中选购一盏，问选哪一种灯合算？
⑶小明想在这两种灯中选两盏，假定照明时是3000小时，请你帮助他设计费用最低的选灯方案，并说明理由。（9分）
28、如图，在矩形ABCD中，对角线AC的长为10，且AB、BC（AB＞BC）的长是关于的方程
的两根。
⑴求
的值；
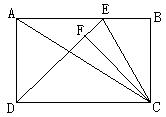⑵若E是AB上一点，CF⊥DE于F，求AE为何值时，△CEF的面积是△CED的面积的
。（8分）
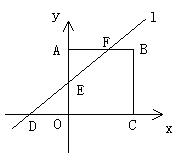29、如图，ABCO是正方形，B（2，2），过D（－2，0）作直线
交OA于E，AB于F，若△DOE≌△FAE，求直线的解析式。若把正方形改为正三角形，即△AOB是正三角形，点B（2，0），过点C（－2，0）作直线交AO于D，交AB于E，且使△ADE的面积和△DCO的面积相等，求直线的解析式。（9分）