中考数学试卷（课改实验区用）
（考试时间共120分钟，全卷满分120分）
一、选择题（本大题共8小题，每小题3分，满分24分）
1．点P（
，1）在（ ）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
2．计算
所得的正确结果是（ ）
A．9 B．
C．
D．6
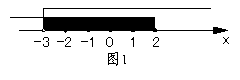
3．如图1所示，图中阴影部分表示
的取值范围，则下列表示中正确的是（ ）
A．
B．
C．
D．
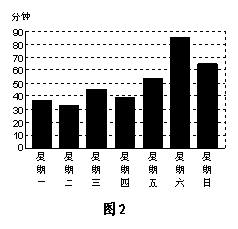
4．小红为了了解自己的学习效率，对每天在家
完成课外作业所用的时间做了一周的记录，并用
图表的形式表示了出来，如图2所示，那么，她
用时最多的一天是（ ）
A．星期一 B．星期三
C．星期四 D．星期六
5．在下列的计算中，正确的是（ ）
A．
B．
C．
D．
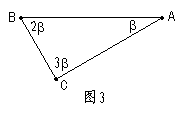
6．如图3所示，则△ABC的形状是（ ）
A．锐角三角形 B．钝角三角形 C．直角三角形 D．等腰三角形
7．把一张形状是多边形的纸片剪去其中某一个角，剩下的部分是一个四边形，那么这张纸片原来的形状不可能是（ ）
A．六边形 B．五边形 C．四边形 D．三角形
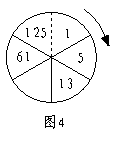
8．请你认真观察和分析图4中数字变化的规律，
由此得到图中所缺的数字应为（ ）
A．32 B．29 C．25 D．23
二、填空题（本大题共10小题，每小题2分，满分20分）
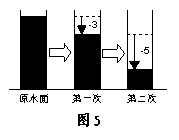
9．水位上升用正数表示，水位下降用负数表示．
如图5所示，水面从原来的位置到第二次变化
后的位置，其变化值是______．
10．化简：
___________．
11．计算：
______________．
12．分解因式：
_____________．
13．如果
，那么
__________．
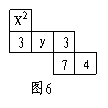
14．如图6是一个正方体的侧面展开图，如果将它折叠成一个
正方体后相对的面上的数相等．则图中的值为______________．
15．请你写出一个图象位于第二和第四象限的反比例函数的
表达式：______________________________．
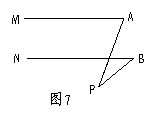
16．如图7，直线MA∥NB，∠A=70°，∠B=40°．
则∠P=____________．
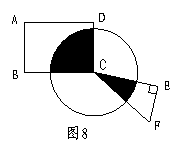
17．如图8，四边形ABCD是一个矩形，⊙C的半径是
2cm，CF=4cm，EF=2cm．则图中阴影部分的面积约
为___________cm2（精确到0.1cm2）．
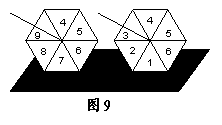18．如图9所示，小李和小陈做转陀螺游戏，他们
同时分别转动一个陀螺，当两个陀螺都停下来时，
与桌面相接触的边上的数字都是奇数的概率是_____．
三、（本大题共2小题，每小题6分，满分12分）
19．（本题满分6分）
解分式方程：
．
20．（本题满分6分）
如图10，PA、PB是圆O的两条切线，A、B是切点，连结AB，直线PO交AB于点M．
请你根据圆的对称性，写出△PAB的三个正确的结论．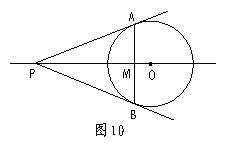
结论⑴：
结论⑵：
结论⑶：
四、（本大题共4小题，每小题8分，满分32分）
21．（本题满分8分）
今年体育中考前，03（2）班的小李、小黄两位同学进行了8次立定跳远训练测试，她们的成绩分别如下：（单位：m）
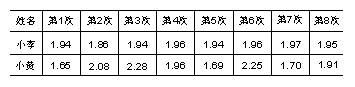
⑴小李和小黄这8次训练的平均成绩分别是多少？
⑵按规定，女同学立定跳远达到1.94m 就可以得到该项目满分6分．如果按她们目前的水平参加考试，你认为小李与小黄在该项目上谁得6分的可能性更大些？请说明理由．
22．（本题满分8分）
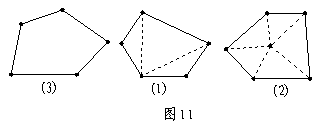
小明和小亮分别利用图11中⑴、⑵的不同方法求出了五边形的内角和都是540°．请你考虑在图⑶中再用另外一种方法求五边形的内角和，并写出求解的过程．
23．（本题满分8分）
某校八年级在学校团委的组织下，围绕“八荣八耻”开展了一次知识竞赛活动．竞赛规则：每班代表队都必须回答27道题，答对一题得5分，答错或不答都倒扣1分．
⑴在比赛到第18题结束时，03（3）班代表队得分为78分，这时03（3）班代表队答对了多少道题？
⑵比赛规定，只有得分超过100分（含100分）时才能获奖．03（3）班代表队在比赛到第18题结束时得分为78分，那么在后面的比赛中至少还要答对多少道题才有可能获奖？请简要说明理由．
24．（本题满分8分）
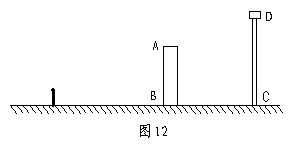
如图12，一天早上，小张正向着教学楼AB走去，他发现教学楼后面有一水塔DC，可过了一会抬头一看：“怎么看不到水塔了？”心里很是纳闷．经过了解，教学楼、水塔的高分别是20m和30m，它们之间的距离为30m，小张身高为1.6m．小张要想看到水塔，他与教学楼之间的距离至少应有多少米？
五、（本大题共2小题，每小题10分，满分20分）
25．（本题满分10分）
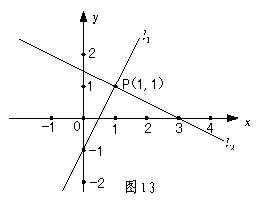
请你根据图13中图象所提供的信息，解答下面问题：
⑴分别写出
、
中变量
随变化而变化的情况；
⑵求出一个二元一次方程组，使它满足图象中的条件．
26．（本题满分10分）
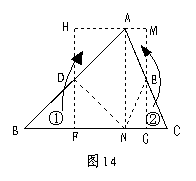
任意剪一个三角形纸片，如图14中的△ABC，不妨设它的一个锐角为∠A，首先利用对折的方法得到高AN．然后按图中所示的方法分别将含有∠B、∠C的部分向里折，找出AB、AC的中点D、E，同时得到两条折痕DF、EG，分别沿折痕DF、EG剪下图中的三角形①、②，并按图中箭头所指的方向分别旋转180°．
⑴你能拼成一个什么样的四边形？并说明你的理由；
⑵请你利用这个图形，证明三角形的面积公式：
．
六、（本大题共1题，满分12分）
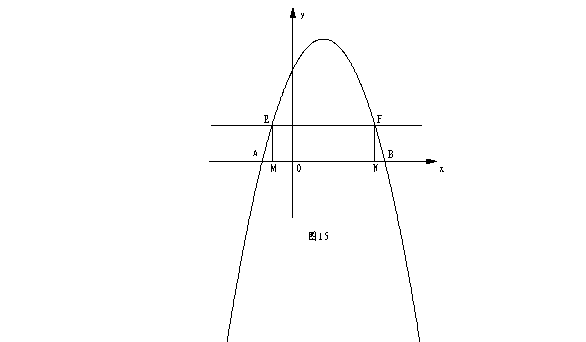
27．如图15，抛物线
的图象与轴交于A（
，0）、B两点，在轴上方且平行于轴的直线EF与抛物线交于E、F两点，E在F的左侧，过E、F分别作轴的垂线，垂足是M、N．
⑴求m的值及抛物线的顶点坐标；
⑵设BN = t ，矩形EMNF的周长为C，求C与t的函数表达式；
⑶当矩形EMNF的周长为10时，将△ENM沿EN翻折，点M落在坐标平面内的点记为M′，试判断点M′是否在抛物线上？并说明理由．
