《一次函数》单元考试卷
班级： 姓名： 座号： 评分：
说明：本卷满分100分，另外附加题20分
一、选择题（6×4=24分）
1、下面哪个点不在函数
的图象上（ ）
A.（-5，13） B.（0.5，2） C（3，0） D（1，1）
2、下列关系式中，表示y是x的正比例函数的是（ ）
A、 y=
B、 y=2x
C、 y=x＋1 D、 y=2x
3、直线y=kx＋b经过二、三、四象限,则k、b应满足( )
A、k>0, b<0; B、k>0,b>0; C、k<0, b<0; D、k<0, b>0.
4、函数y=4x－2与y=－4x－2的交点坐标为（ ）
A、（－2，0） B、（0，－2） C、（0，2） D、（2，0）
|
|
|
|
 |
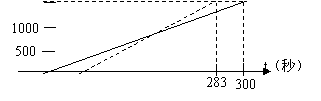（图中实线为甲的路程与时间的关系图象，虚线为乙的路程与时间的关系图象）小王根据图象得到如下四个信息，其中错误的是（ ）
A 这是一次1500米的赛跑 B 甲、乙两人中乙先到达终点
C 甲、乙同时起跑 D 甲的这次赛跑中的速度为5米/秒
6、已知点A（-2，y1）、B（2，y2）在同一条直线y=-2x+b上，则y1 与 y2的关系为（ ）
A、 y1 ＜ y2 B 、 y1 ＞ y2 C 、 y1 =y 2 D、无法确定
二、填空题（每空3分，共48分）
1、关系式y=43x+1的变量是 ，常量是 。
2、正比例函数y=kx的图象经过点（3，6）,则k= 。
3、函数y=－
的自变量x的取值范围_______________
4、直线y=2x向 平移 个单位可得直线y=2x+5。
5、小华用500元去购买单价为5元的一种商品，剩余的钱y（元）与购买这种商品的件数x（件）之间的函数关系是______________， x的取值范围是__________
6、y=－2x＋4的图象经过___________象限，它与两坐标轴围成的三角形面积为_________，
7、函数
的图象与y轴的交点是
，与x轴的交点是
。
8、已知一次函数
，当 m ，y随x的增大而增大。
9、一次函数
的图象经过点（-3，0）,则k= 。
10、函数y=2x－4，当x_______，y<0.
11、若点（m，m＋3）在函数y=－
x＋2的图象上，则m=____
三、解答题
1、已知一次函数的图象经过点（－3，2）和点（2，－3），
（1） 求一次函数的解析式；（8分）
（2） 判断点（－2，5）是否在该函数图象上。（4分）
2、某影碟出租店要设两种租碟方式：一种是零星租碟，每张收费1元；另一种是会员卡租碟，办卡费每月12元，租碟费每张0.4元,小彬常来租碟,若每月租碟数量为x张,
(1) 写出零星租碟方式应付金额y1(元)与租碟数量x(张)之间函数关系式;（6分）
(2) 写出会员卡租碟方式应付金额y2(元)与租碟数量x(张)之间的函数关系式; （6分）
(3) 小彬选取哪种方式更合算? （4分）
四、附加题（4×5=10分）
1、函数y=
的自变量x的取值范围是（ ）
A．x
B．x
1 C．x>1 D．x且x1
2、函数
与
的图像交于
轴，则m= 。
3、一次函数y=k1x-4与正比例函数y=k2x的图象经过点（2，-1），则这两个函数的图象与x轴围成的三角形的面积是
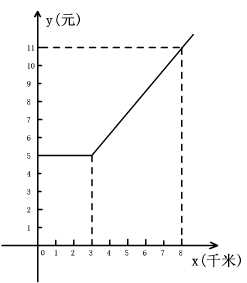
4、.如图是某出租车单程收费y(元)与行驶路程x(千米)之间的函数关系图象,根据图象回答下列问题
(1)当行使8千米时,收费应为 元
(2)求出收费y(元)与行使x(千米)(x≥3)之间的函数关系式