初三毕业模拟数学试题
A卷（100分）
一、选择题（每小题3分，共24分）
1、某勘探队在A、B、C、D四处的标高为A(-47.5m)，B(0m)，C(-139.7m)，D(5.7m)，其中最高处和最低处分别是（ ）
(A) (C)、(B) (B) (D)、(B) (C) (D)、(C) (D)无法比较
2、下列计算中，正确的是（ ）
(A)a8÷a4=a2
(B)(a2)3=a5 (C) -3=
-3 (D)
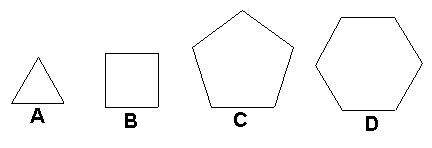3、如图，在下面四种正多边形中，用同一种图形不能平面镶嵌的是（ ）
4、如图，对a、b、c三种物体的重量判断正确的是（ ）
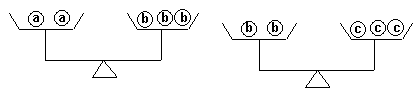(A) a<c (B)
a<b (C)
a>c (D) b<c
5、如图，梯子跟地面的夹角为∠A，关于∠A的三角函数值与梯子的倾斜程度之间，叙述正确的是（ ）
(A)sinA的值越小，梯子越陡
(B) cosA的值越小，梯子越陡
(C) tan A的值越小，梯子越陡 (D)陡缓程度与∠A的三角函数值
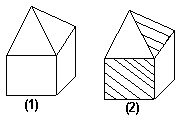
6、图1是由白色纸板拼成的立体图形，将此立体图形中的两面涂上颜色，如图2，图3中的四个图形中（ ）是图2的展开图
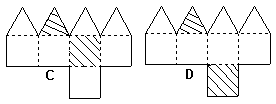
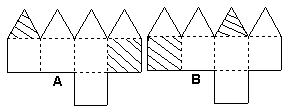
7、某村办工厂今年前5个月生产某种产品的总量c（件）关于时间t（月）的图象如图所示，则该厂对这种产品来说（ ）
(A)1月至3月每月生产总量逐月增加，4、5两月生产总量逐月减少
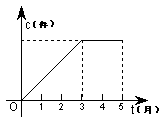(B) 1月至3月每月生产总量逐月增加，4、5两月生产总量与3月持平
(C) 1月至3月每月生产总量逐月增加，4、5两月均停止生产
(D) 1月至3月每月生产总量不变，4、5两月均停止生产
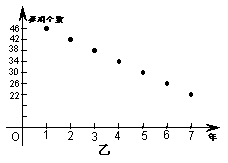
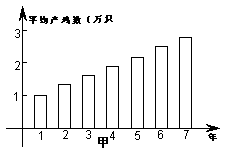
8、甲、乙两人连续7年调查某县养鸡业的情况。提供了两方面的信息图（如图）甲调查表明：养鸡场的个数从第1年的1万只上升到第7年的2.8万只；乙的调查表明：养鸡场的个数由第1年的46个减少到第7年的22个.
现给出下列四个判断：①该县第2年养鸡场产鸡的数量为1.3万只；②该县第2年养鸡场产鸡的数量低于第1年养鸡场产鸡的数量；③该县这7年养鸡场产鸡的数量逐年真增长；④这7年中，第5年该县养鸡场产鸡的数量最多，根据甲、乙两人提供的信息，可知其中正确的判断有（ ）个
(A) 2 (B) 1 (C) 0 (D) 3
二、填空题（每小题3分，共24分）
9、函数
中，自变量x的取值范围是
.
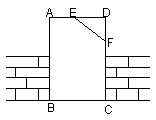10、如图，工人师傅砌砖门时，常用木条EF固定矩形门框ABCD，使其不变形，这种做法的根据是
.
11、△ABC中，∠C=90°，∠A、∠B、∠C所对的边分别为a、b、c，且c=3b，则cosA等于 .
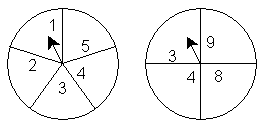
12、如图所示的两个转盘分别被均匀地分成5个和4个扇形，每个扇形上都标有数字，同时自由转动两个转盘，转盘停止后，指针都落在奇数的概率是 .
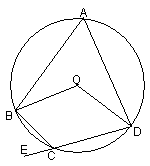13、如图，四边形ABCD为⊙O的内接四边形，点E在DC的延长线上，如果∠BOD=120°，那么∠BCE等于
14、在直角梯形ABCD中，AD∥BC，AB⊥AD，
，AD、BC的长是方程x2-20x+75=0的两根，那么以D为圆心，AD为半径的圆与以点C为圆心，BC为半径的圆的位置关系是 .
15、已知二次函数的图象如图所示，则在“①a<0；②b>0；③c<0；④b2-4ac”中，正确的判断是
（填序号）
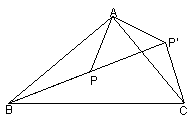16、如图，△ABC是直角三角形，BC是斜边，将△ABP绕点A逆时针旋转后，能与△ACP′重合，已知AP=3，则PP′的长度为
.
三、解答题（每小题6分，共18分）
17、计算：
18、如图，已知四边形ABCD是等腰梯形，AB=DC，AD∥BC，PB=PC.
求证：PA=PD .
19、阅读下题的解答过程，请你判断其是否有错误，若有错误，请你写出正确答案.
已知：m是关于x的方程mx2 - 2x+m=0的一个根，求m的值
解：把x=m代入方程，化简得m3=m，两边同时除以m，得m2=1，所以m=1，把m=1代入原方程检验可知：m=1符合题意 .
答：的值是1 .
四、（20题9分，21题8分，共17分）
20、一张卡片的正面写有数字1，背面写有数字2；另一张卡片的正面写有数字4，背面写有数字6. 用这两张卡片排成两位数，正、被两面的任意一面朝上. 求：（1）排成的两位数是奇数的概率；（2）得到的数是7的倍数的机会和得到的两位数是奇数的机会哪个大？
21、在一次暖气管道的铺设工作中，工程由A点出发沿正西方向进行，在A点的南偏西60°方向上有一所学校B，如图，占地是以B为中心方圆100m的圆形，当工程进行了200m后到达C处，此时B在C南偏西30°方向上，请根据题中所提供的信息计算并分析一下，工程若继续进行下去是否会穿越学校.
五、（8分）
22、如图，一次函数与反比例函数的图象分别是直线AB和双曲线，直线AB与双曲线的一个交点为C，CD⊥x轴于D，OD=2OB=4OA=4,求一次函数和反比例函数的解析式.
六、（9分）
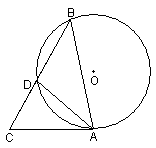23、如图，已知AC切⊙O于A，CB顺次交⊙O于D、B两点，AC=6，BD=5. 连接AD，AB（1）证明：△CAD∽△CBA；（2）求线段DC的长.
B卷（50分）
一、填空题（每小题3分，共18分）
24、若关于x的一元二次方程x2+x - 3m=0有两个不相等的实数根，则m的取值范围是 .
25、在直线
上，到x轴或y轴的距离为1的点有
个.
26、某银行设立大学生助学贷款，6年期的贷款年利率为6%，贷款利息的50%由国家财政贴补，某大学生预计6年后能一次性偿还2万元，则他现在可以贷款的数额是 万元（保留2个有效数字）.
27、如图，一个窗户被装饰挡住一部分，其中窗户的长与宽之间的比为3∶2，装饰布由一个半圆和两个四分之一圆组成，圆的直径都是
，这个窗口未被遮挡部分的面积为 .
28、设直线
（n为自然数）与两坐标轴围成的三角形面积为（n=1，2，……2006），则S1+S2+…+S2006的值为 .
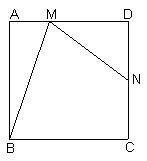29、如图，正方形ABCD中，N是DC的中点，M是AD上异于D的点，且∠NMB=∠MBC，则tan∠ABM= .
二、实际应用（9分）
30、某书店进行优惠促销活动，实行两种优惠方法：一是九折优惠卡，凡在书店购书的按九折优惠；二是积分卡，凡在书店购书金额积满100元的积分为1分，一年内积分满2分的，赠购书券20元；积分满5分的，赠购书券75元；积分满10分的，赠购书券200元. （注：用所赠购书券购书时，不再优惠，每次购书时只能使用一种卡）.
（1）以上两种优惠卡中，积分卡的优惠方法，可用如下形式表达：设购书金额为x元，优惠金额为y元，则：
①当200≤x<500时，y=20；②500≤x<1000时，y= ；③x≤ 时，y=200（各1分）
（2）某人在此书店先后用两种不同的优惠卡进行购书都得到了优惠，所得优惠金额共计45元，请你估计此人购书的金额至少应为多少元？并求出购书金额的范围（4分）
（3）假设某人一年购书金额约为500元左右，请问使用何种优惠卡购书更省钱（3分）
三、（11分）
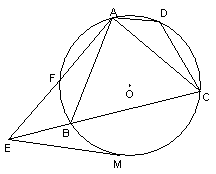
31、如图，已知四边形ABCD内接于⊙O，A是弧BDC的中点，AE⊥AC于A，与⊙O及CB的延长线分别交于点F、E，且弧BF等于弧AD，EM切⊙O于M .
（1）求证：△ADC∽△EBA（3分）；
（2）求证：
（3分）；
（3）如果AB=4，EM=6，求cot∠CAD的值（5分）
四、（12分）
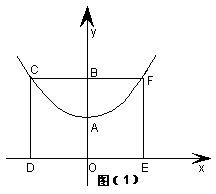
32、如图1所示，已知抛物线的顶点为A（0，1），矩形CDEF的顶点C、F在抛物线上，D、E在x轴上，CF交y轴于点B（0，2），且其面积为8.
（1）求此抛物线的解析式；
（2）如图2所示，若P点为抛物线上不同于A的一点，连接PB并延长交抛物线于点Q，过点P、Q分别作x轴的垂线，垂足分别为S、R .
①求证：PB=PS；
②判断△SBR的形状；
③试探索在线段SR上是否存在点M，使得以点P、S、M为顶点的三角形和以点Q、R、M为顶点的三角形相似，若存在，请找出M点的位置；若不存在，请说明理由.
