初三第一学期月考数学试卷
卷一
一、选择题 （本题有12小题，每小题4分，共48分）
1. 函数
是
（
）
A、一次函数 B、二次函数 C、正比例函数 D、反比例函数
2. 要使二次根式
有意义，那么x的取值范围是
（ ）
A、x＞－1 B、 x＜1 C、 x≥1 D、 x≤1
3．抛物线y＝（x－12）2＋6的顶点坐标是
（ ）
A、（－12，6） B、（12，－6） C、（12，6） D、（－12，－6）
4.下列二次根式中，是最简二次根式的是 （ ）
A 
B
Ｃ
Ｄ
5．在Rt△ABC中，∠ACB＝90o，CD⊥AB于点D，
AC＝6，AB＝9，则AD的长是 ( )
A、6 B、5 C、4 D、3
6．已知x1、x2是方程x2－3x－１＝０的两根，则x1·x2＝ （ ）
Ａ －１ Ｂ 3 Ｃ－3 Ｄ １
7．已知
，那么下列等式中一定成立的是
（ ）
A、x＝
y B、9x＝7y C、7x＝9y
D、xy＝63
8. 已知方程x2－5x＝2－
, 用换元法解此方程时，可设y＝,
则原方程化为 （ ）
A、y2－y＋2＝0 B、y2－y－2＝0 C、y2＋y－2＝0 D、y2＋y＋2＝0
9. 如图，△ABC中，D、E分别在AB、AC上，且DE∥BC，
若AE∶EC＝1∶2，AD＝6，
则AB的长为 （ ）
A、18 B、12 C、9 D、3
10．将抛物线y＝2x2向左平移1个单位,再向上平移3个单位得到的抛物线,
其解析式是 ( )
A、y＝2(x＋1)2＋3 B、 y＝2(x－1)2－3
C、 y＝2(x＋1)2－3 D、 y＝2(x－1)2＋3
．11．根据下列表格的对应值：
| x | 3.23 | 3.24 | 3.25 | 3.26 |
|
| －0.06 | －0.02 | 0.03 | 0.09 |
判断方程
(a≠0，a，b，c为常数)一个解x的范围是 （ ）
A、3＜x＜3.23 B、3.23＜x＜3.24 C、3.24＜x＜3.25 D、3.25 ＜x＜3.26
12．设“●、■、▲”分别表示三种不同的物体，如图所示，前两架天平保持平衡，如果要使第三架也平衡，那么“？”处应放“■”的个数为 ( )
A、5 B、4 C、3
D、2
卷二
二、填空题（本题有六小题，每小题5分，共30分）
13. 化简：
_____.
14. 已知二次函数y＝x2＋2x＋c的图象经过点(0,1)，则c＝_____.
15. 如果
，那么
_______ ．
16. 如图：已知：AE=4，EC=2，AD=3，当AB=__________时，△ABC～△AED。
17.若二次函数
，当x取
，
（≠）时，函数值相等，
则当x取+时，函数值为 。
18．在Rt△ABC中，∠ACB=90°，CD⊥AB于D,AD和BD是方程x2－5x＋4＝0的根，则△ABC的面积等于 。
三、解答题 （本题共有7小题，共72分）以下各小题必须写出解答过程。
19. （本小题8分）计算:
+ 
20.（本小题8分）解方程 
=3
21（本小题10分）．如图，用长为18 m的篱笆（虚线部分），两面靠墙围成矩形的苗圃.
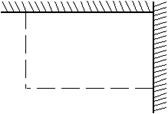（1）设矩形的一边为
（m），面积为
(m2)，求关
于的函数关系式，并写出自变量的取值范围；
（2）当为何值时，所围苗圃的面积最大，最大面积是多少？
22、（本题10分）
如图，在平面直角坐标系中，正方形AOCB的边长为6，O为坐标原点，边OC在x轴的正半轴上，边OA在y轴的正半轴上，E是边AB上的一点，直线EC交y轴于F，且
S△FAE∶S四边形AOCE＝1∶3。
⑴、求出点E的坐标；
⑵、求直线EC的函数解析式
23、（本题12分）如图，在4×4的正方形方格中，△ABC和△DEF的顶点都在
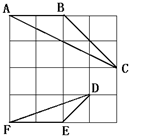边长为1的小正方形的顶点上.
（1）填空：∠ABC= °，BC= ；
（2）判断△ABC与△DEF是否相似，并证明你的结论.
（3）你能在方格中找出几个三角形与△DEF全等？(写出答案即可)
24．(本题12分) 已知抛物线经过Ａ（－３，０），Ｂ（０，３），Ｃ（２，０）三点。
（１）求这条抛物线的解析式；（２）求出抛物线顶点坐标和对称轴；（３）已知点Ａ（４，２），试判断点Ａ是否在抛物线上。
25. (本题12分) 已知四边形ABCD中，P是对角线BD上的一点，过P作MN∥AD，EF∥CD，分别交AB、CD、AD、BC于点M、N、E、F，设a=PM·PE，b=PN·PF。解答下列问题：
(1)、当四边形ABCD是矩形时，见图1，请判断a与b的大小关系，并说明理由；
(2) 、当四边形ABCD是平行四边形，且∠A为锐角时，见图2，（1）中的的结论是否成立？请说明理由；（3）、在（2）的条件下，设 ，是否存在这样的实数k，使得 ？若存在，请求出满足条件的所有k的值；若不存在，请说明理由。