初三级数学第一学期期末测试题

说明：全卷共8页，考试时间90分钟，满分150分

一、填空题（每小题3分，共42分）

1、－4的绝对值是________。

2、计算：2a⁷÷a² =_____。

3、分解因式：y²- y =_________。

4、一元二次方程x²+5x+6=0的解是___________。

5、函数y=中x的取值范围是____________。

6、等腰三角形的两条边长分别为1和2，则它的周长为______。

7、若梯形的中位线长为3cm，高是2cm，则这个梯形的面积是______。

8、写出一个经过第一、三象限的正比例函数是____________。

9、不等式4x+1>2x-1的解集是___________。

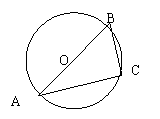
10、如下图，⊙O的半径OA=5cm，弦心距OC=3cm,则弦AB=____cm .

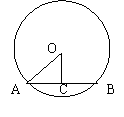　　　　（第10题）　　　　　　  （第11题）

11、如上右图，⊙O的直径AB=10cm ，C是⊙O上一点,∠ABC=60⁰，则BC=____cm.

12、若两个相似三角形的相似比为3∶4，则这两个三角形周长的比是____。

13、计算：2Sin30⁰+tan60⁰=____。

14、观察等式：1+3=4=2²，1+3+5=9=3²，1+3+5+7=16=4²，1+3+5+7+9=25=5²……　

　　　可以发现，从1开始，n个连续奇数的和等于____

二、选择题：（每小题3分，共18分）

15、用科学记数法表示25000为　　　　　　　　　　　　　　　　 （　　 ）

A、2.5×10^—3 B、25×10³　 C、2.5×10⁴　　D、0.25×10⁵

16、下列命题正确的是　　　　　　　　　　　　　　　　　　　　 （　　 ）

　　A、5和-互为倒数； B、单项数2×10⁵x²y的次数是8；

C、实数和数轴上的点一一对应；D、过平面上的三点可作一个圆.

17、顺次连结四边形各边中点所得的四边形是　　　　　　　　　　　 (　　 )

　　 A、平等四边形　　　B、矩形　　 C、正方形　　D、梯形

18、如下图，PT是⊙O的切线，PAB是⊙O的割线，且PT=4，PA=2，则AB=（　　）

　　 A、8　　　 B、4　　　 C、2　　　D、6

19、在抛物线y = - x²+ 1 上的点是　　　　　　　　　　　　　　  （　　 ）

　　 A、 （-1，1）　　B、（ ，1）　 C、（-3，2）  D、（2，-3）

20、如果b>0，c>0，那么二次函数y = ax² + bx + c 的图像如下图所示大致是（　　）

　　

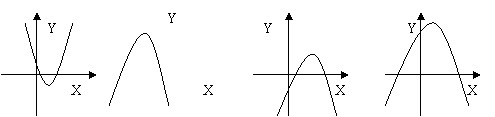
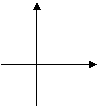
　　　　 A　　　　　　 B　　　　　　　　 C　　　　　　　　 D

三、解答下列各题（每小题6分，共30分）

　 21、计算：（-2）² +（⁺）⁰ ＋２^－１-

　 22、先化简，再求值：- ，其中x=

23、解二元二次方程组　　 x ²+ y = 5

　　　　　　　　　　　　 y - 3x + 5 = 0

24、甲、乙两班学生绿化校园，如果单独工作，乙班比甲班多用5天；如果两班合作，6天可以完成。两班单独工作各需多少天完成？

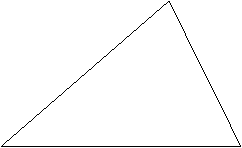
25、校园内有一块如下图的三角形空地，要在空地内建一个最大的圆形花坛，你会在三角形内作出吗？请试一试。（尺规作图，不写作法和证明）

四、（每小题8分，共40分）

26、用换元法解方程：（）² + 6 = 5（）

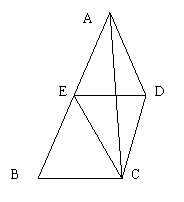
27、已知：如图，ED∥BC，ED=BC，且E为AB的中点。

　 （1） 求证：△AED≌△EBC　（4分）

　 （2） 观察图形，在不添加其他线的情况下，除△EBC外，请写出两个与△AED的面积相等的三角形（直接写出结果，不要证明）。（4分）

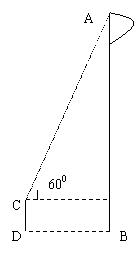
28、某同学用一个有60⁰角的直角三角板估测学校旗杆AB的高度，他将60⁰角的直角边水平放在1.5米高的支架CD上，三角板的斜边与旗杆的顶点在同一直线上，他又量得D、B的距离为5米，求旗杆AB的高度。（精确到1米，取1.73）

29、一家电信公司给顾客提供两种上网收费方式：方式A以每分0.1元的价格按上网时间计费；方式B除收月基费20元外再以每分0.05元的价格按上网时间计费.

（1）如果设上网时间为x分，按方式A收费为y₁ 元，按方式B收费为y₂元，则y₁=___________，y₁ =__________。（2分）

（2）如何选择收费方能使上网者更合算？（6分）

30、已知关于x的方程X² + （4K + 1）X + 2K- 1 = 0

　 （1）求证：此方程一定有两个不相等的实数根；（4分）

　 （2）若X₁ ，X₂是方程的两个实根，且（X₁-2）（X₂-2）=2K-3，求K的值。

（4分）

 

五、（每小题10分，共20分）

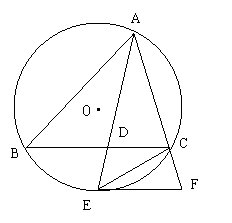31、如图，△BAC内接于⊙O，∠BAC的平分线交BC于D，交⊙O于E，EF∥BC交AC的延长线于F，连结CE.

求证:(1)∠BAE=∠CEF；（5分）

(2)EF是⊙O的切线。（5分）

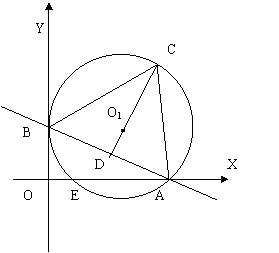
32、如图，已知直线y = x + 1与x轴、y轴分别交于A、B两点，以AB为边在第一象限内作正三角形ABC，⊙O₁为△ABC的外接圆，与x轴交于另一点E .

　　（1）求A、B、C点坐标；（3分）

　　（2）求过C点与AB中点D的一次函数的解析式；（3分）

　　（3）求过E、O₁、A三点的二次函数的解析式。（4分）