初三年级第一次模拟考试数学试卷
(考试时间：120分钟 试卷满分：150分 考试形式：闭卷)
一、选择题：(本大题共10小题，每小题3分，计30分)
1、若家用电冰箱冷藏室的温度是4°C，冷冻室的温度比冷藏室的温度低22°C，则冷冻室的温度是 ( )
A、—26°C B、—18°C C、26°C D、18°C
2、下列运算中，错误的是 ( )
A、a·a2＝a3 B、2a＋3b＝6ab C、a4÷a3＝a D、(—ab)4＝a4b4
3、如果ab
0，则
的值不可能是 ( )
A、2 B、—2 C、0 D、1
4、下列关于
的说法中，错误的是 ( )
A、是无理数 B、3＜＜4
C、是12的算术平方根 D、是最简二次根式
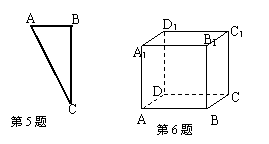
5、如图，△ABC的三个顶点均在4×4的正方形格点上，则∠ACB的度数 ( )
A、等于30° B、大于30° C、小于30° D、大于40°
6、如图所示的长方体中，与平面A1C1垂直的平面共有 ( )
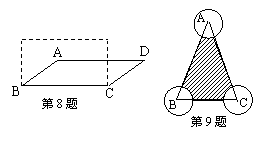A、4个
B、3个
C、2个 D、1个
7、随着通讯市场竞争的日益激烈，某通讯公司的手机市话收费按原标准降低了a元后，再次下调了25%，现在的收费标准是每分钟b元，则原收费标准每分钟为 ( )
A、
B、
C、
D、
8、如图，若将四根木条钉成的矩形木框变形为平行四边形ABCD的形状，并使其面积为矩形面积的一半，则这个平行四边形的一个最小内角的值等于 ( )
A、30° B、45° C、60° D、90°
9、如图，圆A、圆B、圆C两两不相交，且它们的半径都是1cm，AB＝AC＝4cm，BC＝3cm，则图中阴影部分图形的周长为 ( )
A、11cm
B、(5＋
)cm C、(5＋2)cm D、(6＋)cm
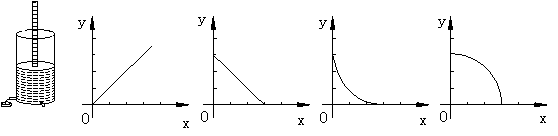
10、如图，是一种古代计时器――“漏壶”的示意图，在壶内盛一定量的水，水从壶下的小孔均匀漏出，壶内壁标有刻度，人们根据壶中水面的刻度计算时间，用x表示时间，y表示壶底到水面的高度，则适合表示一小段时间内y与x之间函数关系的图像是( )
 |
|
二、填空题：(本大题共8小题，每小题3分，计24分.)
11、某种细菌的直径是1.6×10—5cm，则1.6×10—5 0..(填“＞“或“＜”)
12、一元二次方程(x＋1)2 ＝0的根为 .
13、受国际油价上涨的影响，某地今年四月份93号汽油的价格是每升3.80元，五月份93号汽油的价格每升3.99元，则四月到五月93号汽油的价格上涨的百分数是 .
14、如图，有一条直的等宽纸带，按图中折叠时，纸带重叠部分中的∠α等于 度.
 |
15、某城市自来水收费实行阶梯水价，收费标准如下表所示，用户5月份交水费45元，则所用水为 吨.
| 月用水量 | 不超过12吨的部分 | 超过12吨不超过18吨的部分 | 超过18吨的部分 |
| 收费标准(元/吨) | 2.00 | 2.50 | 3.00 |
16、如图，Rt
ABC中，
B＝Rt，AB＝3，BC＝6，将RtABC沿BC向右平移2个单位，则图中阴影部分的面积为
.
17、甲、乙两名学生进行射击练习，两人在相同条件下各射靶10次，将射击结果作统计分析如下：
| 命中环数 | 5 | 6 | 7 | 8 | 9 | 10 |
| 甲命中环数的次数 | 1 | 4 | 2 | 1 | 1 | 1 |
| 乙命中环数的次数 | 1 | 2 | 4 | 2 | 1 | 0 |
请你从射击稳定性方面评价甲、乙两人的射击水平，则 比较稳定.
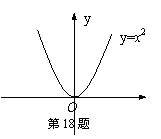
18、如图是y＝x2的图象，我们可以利用y＝x2的图象求
的近似值，请你叙述利用图象求近似值的作图过程(并在图中标出所作的线段及必需的字母)：_______________
___________________________________________________________________________
三、解答题：(本大题共6小题，计40分)
19、(本题满分6分)计算：
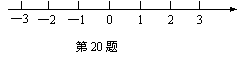
20、(本题满分6分)解不等式组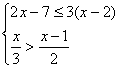
并在数轴上表示出其解集.
21、(本题满分6分)已知关于x的方程
的解是x＝2，其中a0且
，求代数式
的值.
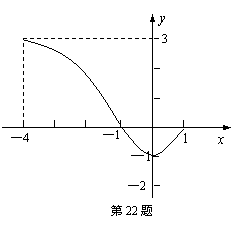22、(本题满分8分)如图，曲线表示某个函数的图象，根据图象写出：
(1)自变量x的取值范围；
(2)函数y的取值范围；
(3)当x＝1，—4时，函数y的值；
(4)使函数值为0时的x的值.
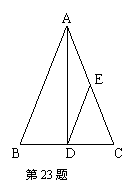23、(本题满分6分)如图，在ABC中，AB＝AC，AD
BC，垂足为D，DE//AB交AC于E，ADE是等腰三角形吗？为什么？
24、(本题满分8分)如图，直角梯形ABCD中，∠D＝∠C＝90°，如果AD＋BC＝AB，
(1)试探索以AB为直径的圆与CD的位置关系，并证明你的结论.
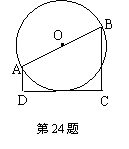(2)若AB＝10，AD＝3，BC＝6，则以AB为直径的圆与CD的位置关系是 (填“相交”、“相切”或“相离”).
四、解答题：(本大题共6小题，计56分)
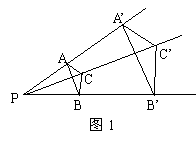
25、(本题满分8分)(1)如图1，已知AB//A’B’，AC//A’C’，
求证：ABC～A’B’C’
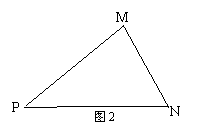(2)如图2，现有一块三角形铁皮MNP，现要截取一个内接等边ABC(即A、B、C三点分别在MNP的三边上)，受第(1)题的启发，你能做到吗？请在图中画出设计图形，并简述画图过程.
26、(本题满分8分)已知ABC的两边AB、AC的长是关于x的方程
的两个实数根，第三边BC的长为5.
(1)k为何值时，ABC是以BC为斜边的直角三角形；
(2)k为何值时，ABC是等腰三角形？并求ABC的周长.
27、(本题满分8分)如图，BD是⊙O的直径，∠1＝∠C，
(1)写出图中所有与ABD相似的三角形：
.
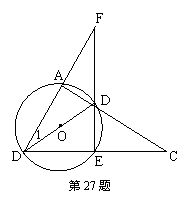(2)探索：设
＝m，是否存在这样的m的值，使得ADF～EDB，请说明理由.
28、(本题满分10分)某市城建部门经过长期市场调查发现，该市年新建商品房面积P(万平方米)与市场新房均价x(千元/平方米)存在函数关系P＝25x；年新房销售面积Q(万平方米)与市场新房均价x(千元/平方米)的函数关系为
(1)如果年新建商品房的面积与年新房销售面积相等，求市场新房均价和年新房销售总额；
(2)在(1)的基础上，如果市场新房均价上涨1千元，那么该市年新房销售总额是增加还是减少？变化了多少？结合年新房销售总额和积压面积的变化情况，请你提出一条合理化的建议.(字数不超过50)
29、(本题满分10分)如图，在直角坐标系xOy中，正方形OABC的边长为2cm，点A、C分别在x轴、y轴的正半轴上，抛物线y＝－x2＋bx＋c经过点B、C.
(1)求抛物线的解析式；
(2)点D、E分别是AB、BC上的动点，且点D从点A开始，以1cm/s的速度沿AB向点B移动，同时点E从点B开始，以1cm/s的速度沿BC向点C移动.运动t秒
(t≤2)后，能否在抛物线上找到一点P，使得四边形BEDP为平行四边形.如果能，请求出t值和点P的坐标；如果不能，请说明理由.
30、(本题满分12分)将一把三角尺放在边长为1m正方形ABCD上，并使它的直角顶点P在对角线AC上滑动，直角的一边始终经过点B，另一边与射线DC相交于点Q，探究：设A、P两点间的距离为x.
(1)当点Q在边CD上时，线段PQ与线段PB之间有怎样的大小关系？试证明你观察得到的结论；
(2)当点Q在CD上时，设四边形PBCQ的面积为y，求y与x之间的函数解析式，并写出自变量x的取值范围；
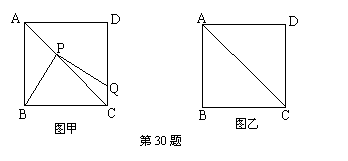(3)当点P在线段AC上滑动时，PCQ是否可能成为等腰三角形？如果可能，指出所有能使PCQ成为等腰三角形的点Q的位置，并求出相应的x的值；如果不能，试说明理由.
| |