数学初中毕业升学考试(非课改卷)
(本试卷共8页,满分120分;考试时间120分钟)
| 题号 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | 总分 | 总分人 | 复分人 |
| 得分 |
亲爱的同学,展示才华的时候到了,相信自己,细心解答,遇到数字运算尽可能使用计算器,定会获得理想的成绩.祝你成功!
一、填空题:本大题共10小题,每小题2分,共20分.请将答案直接写在题中的横线上.
 1.计算:
1.计算:![]() .
.
2.写出![]() 的一个同类项: .
的一个同类项: .
3.已知数据:![]() ,那么这组数据的众数是
,那么这组数据的众数是
.
4.若![]() ,
,![]() ,则代数式
,则代数式![]()
的值是 .
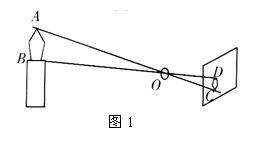
 5.如图1,火焰的光线穿过小孔
5.如图1,火焰的光线穿过小孔![]() ,在竖直的屏幕上形成倒立的实像,像的高度为
,在竖直的屏幕上形成倒立的实像,像的高度为![]() ,
,![]() ,
,![]() ,则火焰的高度是
,则火焰的高度是 ![]() .
.
6.已知一元二次方程![]() 两根的和等于这两根的积,则
两根的和等于这两根的积,则![]() .
.
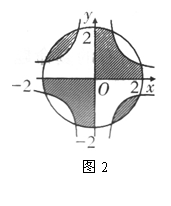
 7.如图2,有反比例函数
7.如图2,有反比例函数![]() ,
,![]() 的图象和一个圆,则
的图象和一个圆,则![]() .
.
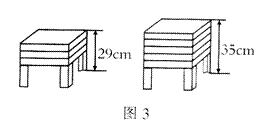
8.商店里把塑料凳整齐地叠放在一起,据图3的信息,当有10张塑料凳整齐地叠放在一起时的高度是 ![]() .
.
 9.某厂前年缴税
9.某厂前年缴税![]() 万元,今年缴税
万元,今年缴税![]() 万元,如果该厂缴税的年平均增长率为
万元,如果该厂缴税的年平均增长率为![]() ,那么可列方程为 .
,那么可列方程为 .
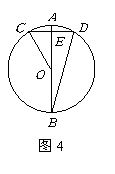
10.如图4,![]() 为
为![]() 的直径,
的直径,![]() 经过弦
经过弦![]() 的中点
的中点![]() ,
,![]() ,则
,则![]() .
.
二、选择题:本大题共8小题,每小题3分,共24分.在每小题给出的四个选项中,只有
一项是符合题意的,请将你认为正确答案的序号填在题后括号内.
11.截至2006年4月15日3时44分,我国神舟六号飞船轨道舱已环绕地球2920圈,用科学记数法表示这个数是( )
A.![]() 圈 B.
圈 B.![]() 圈
圈
C.![]() 圈 D.
圈 D.![]() 圈
圈
12.计算:![]() ,正确的结果是( )
,正确的结果是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 13.不等式组
13.不等式组![]() 的解集是( )
的解集是( )
A.![]() B.
B.![]()
C.![]() 或
或![]() D.
D. ![]()
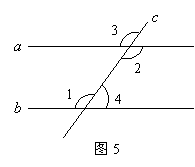
14.如图5,下列条件不能判定直线![]() 的是( )
的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
15.丽丽买了一张30元的租碟卡,每租一张碟后剩下的余额如表6表示,若丽丽租碟25张,则卡中还剩下( )
A.5元 B.10元 C.20元 D.14元
| 租碟数(张) | 卡中余额(元) |
| 1 |
|
| 2 |
|
| 3 |
|
|
|
|
|
16.正比例函数![]() 的图象经过第二、四象限,若
的图象经过第二、四象限,若![]() 同时满足方程
同时满足方程![]() ,则此方程的根的情况是( )
,则此方程的根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.不能确定
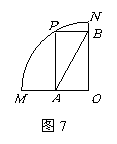 17.如图7,四边形
17.如图7,四边形![]() 是扇形
是扇形![]() 的内接矩形,顶点
的内接矩形,顶点![]() 在
在![]() 上,且不与
上,且不与![]() 重合,当
重合,当![]() 点在
点在![]() 上移动时,矩形
上移动时,矩形![]() 的形状、大小随之变化,则
的形状、大小随之变化,则![]() 的长度( )
的长度( )
A.变大 B.变小
C.不变 D.不能确定
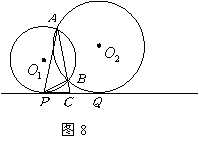 18.如图8,
18.如图8,![]() 与
与![]() 相交于
相交于![]() 两点,直线
两点,直线![]() 与
与![]() 相切于点
相切于点![]() ,与
,与![]() 相切于点
相切于点![]() ,
,![]() 的延长线交
的延长线交![]() 于
于![]() ,连结
,连结![]() ,
,![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() .其中错误的结论有( )
.其中错误的结论有( )
A.3个 B.2个
C.1个 D.0个
三![]() 八为解答题,满分共76分.解答应写出文字说明,证明过程或演算步骤.
八为解答题,满分共76分.解答应写出文字说明,证明过程或演算步骤.
三、本大题共2小题,满分共16分.
19.(本小题满分8分)
计算:![]() .
.
20.(本小题满分8分)
解方程:![]() .
.
四、本大题共2小题,满分共16分.
21.(本小题满分8分)
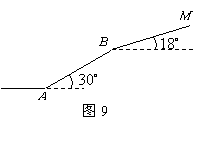
某科技馆座落在山坡![]() 处,从山脚
处,从山脚![]() 处到科技馆的路线如图9所示.已知
处到科技馆的路线如图9所示.已知![]() 处海拔高度
处海拔高度
为![]() ,斜坡
,斜坡![]() 的坡角为
的坡角为![]() ,
,![]() ,斜坡
,斜坡![]() 的坡角为
的坡角为![]() ,
,![]() ,那么科技馆
,那么科技馆![]() 处的海拔高度是多少?(精确到
处的海拔高度是多少?(精确到![]() )
)
 (参考数据:
(参考数据:![]()
![]()
![]()
![]() )
)
22.(本小题满分8分)
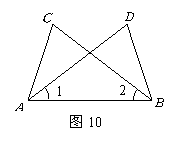
如图10,在![]() 和
和![]() 中,现给出如下三个论断:①
中,现给出如下三个论断:①![]() ;②
;②![]() ;
;
③![]() .
.
请选择其中两个论断为条件,另一个论断为结论,构造一个命题.
 (1)写出所有的真命题(写成“
(1)写出所有的真命题(写成“![]() ”形式,用序号表示):
”形式,用序号表示):
.
(2)请选择一个真命题加以证明.
你选择的真命题是:![]() .
.
证明:
五、本大题共1小题,满分10分.
23.(本小题满分10分)
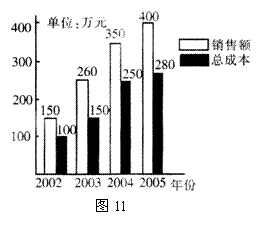
某制衣厂近四年来关于销售额与总成本的统计图,如图11所示.
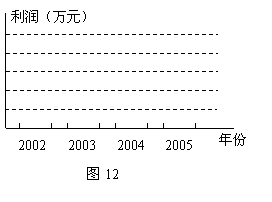
(1)请你在图12中画出四年利润(利润![]() 销售额
销售额![]() 总成本)的统计直方图(要求标出数字);
总成本)的统计直方图(要求标出数字);
(2)根据图11,图12分别写出一条你发现的信息;
(3)若从2004年到2006年这两年间的利润年平均增长率相同,请你预测2006年的利润是多少万元?
 | |||
 | |||
六、本大题共1小题,满分10分.
24.(本小题满分10分)
为鼓励居民节约用水和保护水资源,![]() 市城区从2006年3月1日起,对居民生活用水采取按月按户实行阶梯式计量水价收费,其收费标准是:第一阶梯水价为
市城区从2006年3月1日起,对居民生活用水采取按月按户实行阶梯式计量水价收费,其收费标准是:第一阶梯水价为![]() 元/
元/![]() ;第二阶梯水价为
;第二阶梯水价为![]() 元/
元/![]() .
.
(1)每户人口为4人(含4人)以内的,月用水量![]() 执行第一阶梯水价,月用水量
执行第一阶梯水价,月用水量![]() 的部分执行第二阶梯水价.如果某户人口4人,3月份用水量
的部分执行第二阶梯水价.如果某户人口4人,3月份用水量![]() ,那么应交水费 元;4月份用水量
,那么应交水费 元;4月份用水量![]() ,那么应交水费 元.
,那么应交水费 元.
(2)每户核定人数超过4人的,月用水量![]() (
(![]() 核定人数)执行第一阶梯水阶,月用水量
核定人数)执行第一阶梯水阶,月用水量![]() (
(![]() 核定人数)的部分执行第二阶梯水价,若小江家人口有5人,设月用水量
核定人数)的部分执行第二阶梯水价,若小江家人口有5人,设月用水量![]() ,应交水费
,应交水费![]() 元.
元.
①请你写出![]() 与
与![]() 的函数关系式;
的函数关系式;
 ②若小江家某月交水费
②若小江家某月交水费![]() 元,则该月用水量是多少
元,则该月用水量是多少![]() ?
?
七、本大题共1小题,满分12分.
25.(本小题满分12分)
如图13,已知![]() 是
是![]() 的直径,弦
的直径,弦![]() 于
于![]() ,
,![]() 是
是![]() 上的一点,且
上的一点,且![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,连结
,连结![]() .
.
(1)试判断![]() 的形状(按边分类),并证明你的结论;
的形状(按边分类),并证明你的结论;
(2)若![]() 的半径为
的半径为![]() ,
,![]() ,求
,求![]() 之值.
之值.
八、本大题共1小题,满分12分.
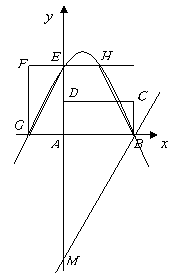
26.(本小题满分12分)
在矩形![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为坐标原点,
为坐标原点,![]() 所在的直线为
所在的直线为![]() 轴,建立直角坐标系.然后将矩形
轴,建立直角坐标系.然后将矩形![]() 绕点
绕点![]() 逆时针旋转,使点
逆时针旋转,使点![]() 落在
落在![]() 轴的
轴的![]() 点上,则
点上,则![]() 和
和![]() 点依次落在第二象限的
点依次落在第二象限的![]() 点上和
点上和![]() 轴的
轴的![]() 点上(如图14).
点上(如图14).
(1)求经过![]() 三点的二次函数解析式;
三点的二次函数解析式;
(2)设直线![]() 与(1)的二次函数图象相交于另一点
与(1)的二次函数图象相交于另一点![]() ,试求四边形
,试求四边形![]() 的周长.
的周长.
(3)设![]() 为(1)的二次函数图象上的一点,
为(1)的二次函数图象上的一点,![]() ,求
,求![]() 点的坐标.
点的坐标.
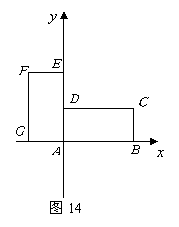 |
初中毕业升学考试
数学试题(非课改)参考答案及评分标准
一、填空题:(每小题2分,共20分)
1.2 2.答案不唯一,如![]() ,
,![]() 3.6 4.2006
3.6 4.2006
5.![]() 6.
6.![]() 7.
7.![]() 8.
8.![]() 9.
9.![]() 10.
10.![]()
二、选择题:(每小题3分,共24分)
11.B 12.D 13.D 14.C 15.B 16.A 17.C 18.C
三、19.解:原式![]() ·············································································· 6分
·············································································· 6分
![]() .································································································ 8分
.································································································ 8分
20.解:![]() .···························································································· 2分
.···························································································· 2分
![]() .·································································································· 4分
.·································································································· 4分
![]() .···································································································· 6分
.···································································································· 6分
检验:当![]() 时,
时,![]() ,
,![]() .
.
![]() 原方程的解为
原方程的解为![]() .··········································································· 8分
.··········································································· 8分
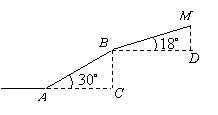 四、21.解:过
四、21.解:过![]() 向水平线
向水平线![]() 作垂线
作垂线![]() ,垂足为
,垂足为![]() ,过
,过![]() 向水平线
向水平线![]() 作垂线
作垂线![]() ,垂足为
,垂足为![]() (如右图),则 2分
(如右图),则 2分
![]() .·························· 4分
.·························· 4分
![]()
![]()
![]() .································································································ 6分
.································································································ 6分
![]() 科技馆
科技馆![]() 处的海拔高度是:
处的海拔高度是:![]() .······ 8分
.······ 8分
22.解:(1)真命题是: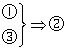 ,
,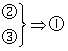 ························································· 4分
························································· 4分
(2)选择命题一: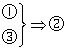
证明:在![]() 和
和![]() 中,
中,
![]() ,
,![]() ,
,![]() ,
,
![]() .································································· 7分
.································································· 7分
![]() .············································································· 8分
.············································································· 8分
选择命题二: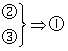
证明:在![]() 和
和![]() 中,
中,
![]() ,
,![]() ,
,![]() ,
,
![]() .································································· 7分
.································································· 7分
![]() .·············································································· 8分
.·············································································· 8分
五、23解:(1)正确画出统计直方图,并标出数字.···················································· 4分
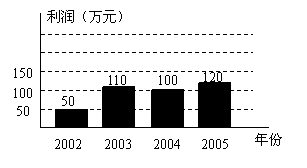
(2)答案不唯一.每写出一条正确的信息给1分.····································· 6分
(3)2004年到2005年的增长率![]() .···················· 8分
.···················· 8分
预测2006年的利润为:![]() (万元).················· 10分
(万元).················· 10分
六、24.解:(1)![]() ,
,![]() ··················································································· 4分
··················································································· 4分
(2)①当![]() 时,
时,![]() ;···················································· 5分
;···················································· 5分
当![]() 时,
时,![]()
![]() .·················································· 7分
.·················································· 7分
②![]() ,可见用水量超过
,可见用水量超过![]() .
.
![]() 当
当![]() 时,
时,![]() .······································ 8分
.······································ 8分
解得![]() .············································································ 9分
.············································································ 9分
![]() 小江家该月用水量为
小江家该月用水量为![]() .··················································· 10分
.··················································· 10分
七、25.(1)解:![]() 是等腰三角形.证明如下:
是等腰三角形.证明如下:
![]() ,
,![]() .························································· 1分
.························································· 1分
![]() .············································································ 2分
.············································································ 2分
![]() ,
,![]() .················································ 3分
.················································ 3分
![]() .
.

![]() 是等腰三角形.······················ 4分
是等腰三角形.······················ 4分
(2)解:连结![]() ,
,![]() .··································· 5分
.··································· 5分
由(1)知![]() ,
,![]() .
.
![]() .·································· 6分
.·································· 6分
![]() .
.
又![]() ,
,
![]() .···································································· 7分
.···································································· 7分
![]() ,即
,即![]() .·································· 8分
.·································· 8分
![]() ,
,
![]() .·········································· 9分
.·········································· 9分
![]() .··································· 11分
.··································· 11分
![]() .··········································································· 12分
.··········································································· 12分
八、26.(1)解:由题意可知,![]() ,
,![]() .······················· 1分
.······················· 1分
![]() ,
,![]() ,
,![]() .······················································ 2分
.······················································ 2分
设经过![]() 三点的二次函数解析式是
三点的二次函数解析式是![]() .
.
把![]() 代入之,求得
代入之,求得![]() .····················································· 3分
.····················································· 3分
![]() 所求的二次函数解析式是:
所求的二次函数解析式是:
![]() .··········································· 4分
.··········································· 4分
(2)解:由题意可知,四边形![]() 为矩形.
为矩形.
![]() ,且
,且![]() .································································· 5分
.································································· 5分
![]() 直线
直线![]() 与二次函数图象的交点
与二次函数图象的交点![]() 的坐标为
的坐标为![]() ,
,
![]() .························································································ 6分
.························································································ 6分
![]() 与
与![]() 与
与![]() 关于抛物线的对称轴对称,
关于抛物线的对称轴对称,
![]() .························································ 7分
.························································ 7分
![]() 四边形
四边形![]() 的周长
的周长
![]()
![]() .····················································································· 8分
.····················································································· 8分
 (3)解法1:设
(3)解法1:设![]() 交
交![]() 轴于
轴于![]() .
.
![]() ,
,
![]() ,
,
即![]() .
.
![]() ,于是
,于是![]() .··················· 9分
.··················· 9分
设直线![]() 的解析式为
的解析式为![]() .
.
把![]() ,
,![]() 代入之,
代入之,
得![]() 解得
解得![]()
![]() .··················································································· 10分
.··················································································· 10分
联合一次,二次函数解析式组成方程组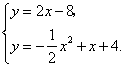
解得![]() 或
或![]() (此组数为
(此组数为![]() 点坐标)
点坐标)
![]() 所求的
所求的![]() 点坐标为
点坐标为![]() .······················································· 12分
.······················································· 12分
解法2:过![]() 作
作![]() 轴于
轴于![]() .由
.由![]() ,得
,得![]() .
.
设所求![]() 点的横坐标为
点的横坐标为![]() ,则纵坐标为
,则纵坐标为![]() .····· 9分
.····· 9分
![]() ,
,![]() ,
,
![]() .··············································································· 10分
.··············································································· 10分
![]() ,
,
![]() ,
,
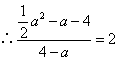 .
.
解之,得![]() 或
或![]() .····································································· 11分
.····································································· 11分
经检验可知,![]() 是原方程的根;
是原方程的根;![]() 是原方程的增根,故应舍去.
是原方程的增根,故应舍去.
当![]() 时,
时,![]() .
.
![]() 所求的
所求的![]() 点坐标为
点坐标为![]() . 12分
. 12分