数学初中毕业升学考试
（考试时间120分钟，满分120分）
一、填空题：本大题共10小题；每小题2分，共20分．请将答案填写在题中的横线上．
1．
的倒数是 ．
2．钟表上8时正时，时针与分针的夹角的补角为 ．
3．用计算器求
的值，结果保留五个有效数字，得 ．
4．函数
的自变量
的取值范围是 ．
5．因式分解：
．
6．如果圆柱的底面半径为2，母线长为3，那么圆柱的侧面积为 ．（答案可保留
）．
7．已知圆
和圆
相切，两圆的圆心距为8cm，圆的半径为3cm，则圆的半径为 cm．
8．市统计局的资料显示，今年第一季度我市的财政收入约为
万元，比去年同期增长
，则去年第一季度我市的财政收入约为 万元（精确到1万元）．
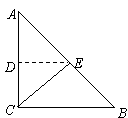9．如图，已知
的面积为50米
，将沿
翻折，使点和点
重合，若折痕恰好平行于
，那么
的面积为 米．
10．如下图所示，由一些点组成形如三角形的图形，每条边（包括两个顶点）有
个点，每个图形总的点数是
，当
时，
．
二、选择题：本大题共8小题；每小题3分，共24分．在每小题给出的四个选项中，只有一项是正确的，请将正确答案前的字母填入题后的括号内，每小题选对得3分，选错、不选或多选均得零分．
11．以下列各组线段为边，能组成三角形的是（ ）
Ａ．1cm，2cm，4cm Ｂ．8cm，6cm，4cm
Ｃ．12cm，5cm，6cm Ｃ．2cm，3cm，5cm
12．不等式组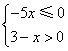
整数解的个数是（ ）
Ａ．1个 Ｂ．2个 Ｃ．3个 Ｄ．4个
13．依次连结菱形各边中点所成的四边形一定是（ ）
Ａ．梯形 Ｂ．菱形 Ｃ．正方形 Ｄ．矩形
14．用换元法解方程
，若设
，则原方程化为关于
的整式方程是（ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
15．等边三角形的外接圆的面积是内切圆面积的（ ）
Ａ．2倍 Ｂ．3倍 Ｃ．4倍 Ｄ．5倍
16．关于的方程
，对其根的情况叙述正确的是（ ）
Ａ．有两个相等的实数根 Ｂ．有两个不相等的实数根
Ｃ．没有实数根 Ｄ．根的情况不能确定
17．若正比例函数
与反比例函数
的图象交于点，且点的横坐标是
，则此反比例函数的解析式为（ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
18．已知
是
的切线，为切点，
是割线，且
是的直径，若
，则
的值为（ ）
Ａ．
Ｂ．
Ｃ．
Ｄ．
三、解答题：本大题共8小题，共76分．
19．（本小题满分6分）
计算：
20．（本小题满分6分）
化简：
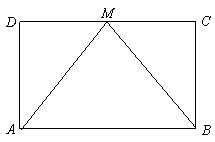21．（本小题满分8分）
如图，在矩形
中，
是
的中点．
求证：
．
22．（本小题满分10分）
（1）（4分）
已知一个样本1，2，3，，5，它的平均数是3，求这个样本的标准差．
（2）（6分）
请列出一组由7个数据组成的数据组，使该组数据的众数、中位数、平均数分别为3，4，5．
23．（本小题满分10分）
“南友高速公路”开通后，南宁至崇左的路程为120千米，本市某单位职工在星期一早上分别乘甲、乙两辆汽车从南宁同时赶往崇左上班，因为甲车每小时比乙车少走20千米，所以甲车比乙车晚12分钟到达崇左，问甲、乙两车平均每小时各走多少千米？
24．（本小题满分10分）
已知二次函数
的图象交轴于
两点，
，交轴的负半轴于点，且
，
，求此二次函数的解析式．
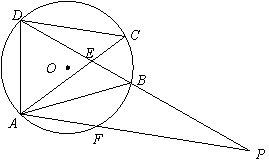
25．（本小题满分12分）
如图，四边形内接于，与
相交于点
，
．
（1）求证：
；
（2）若
是上一点，且
，
的延长线与
的延长线交于点
．
求证：
．
26．（本小题满分14分）
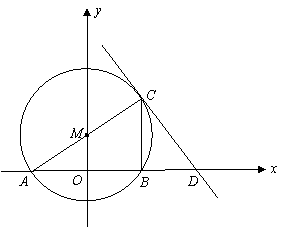如图，在平面直角坐标系中，
与轴交于
两点，是的直径，过点的直线交轴于点
，连结
，已知点的坐标为
，直线的函数解析式为
．
（1）求点的坐标和的长；
（2）求点的坐标和的半径；
（3）求证：是的切线．