数学初中毕业学业考试试卷
考生注意：本科试卷共六个大题，满分120分，考试时量120分钟．
一、填空题（本大题共8个小题，每小题3分，满分24分）
1．
的倒数是 ．
2．在函数
中，自变量
的取值范围是 ．
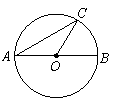
3．如图，
为
的直径，
，则
度．
4．2005年我国自主研制成功发射的神州六号载人飞船，第一次将我国两名航天员送上太空，在太空飞行115小时32分后安全返回预定着落场——内蒙古四子王旗广场，行程米，用科学记数法表示为 米．
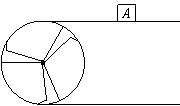
5．如图，一个半径为20cm的转动轮转动
角时，传送带上的物体
平移的距离 是 cm．（结果用含
的式子表示）
 |
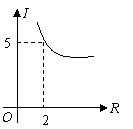
6．在某一电路中，保持电压不变，电流
（安）与电阻
（欧）成反比例关系．其函数图像如图所示，则这一电路的电压为 伏．
7．图案设计，请你用○、△、 材料拼成一幅你认为最漂亮的图形 ．
8．找规律．下列图中有大小不同的菱形，第1幅图中有1个，第2幅图中有3个，第3幅图中有5个，则第
幅图中共有 个．
 |
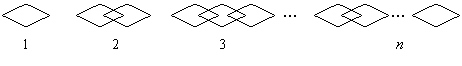二、选择题（本大题共8个小题，每小题3分，满分24分，每小题给出四个选项，选出符合题设要求的一项，将其代号填入对应的题号下）
9．去年娄底市有7.6万学生参加初中毕业会考，为了解这7.6万名学生的数学成绩，从中抽取1000名考生的数学成绩进行统计分析，以下说法正确的是（ ）
A．这1000名考生是总体的一个样本
B．7.6万名考生是总体
C．每位考生的数学成绩是个体
D．1000名学生是样本容量
10．如果
是任意的两个实数，下列式中的值一定是负数的是（ ）
A．
B．
C．
D．
11．用长为5cm，6cm，7cm的三条线段围成三角形的事件是（ ）
A．随机事件 B．必然事件 C．不可能事件 D．以上都不是
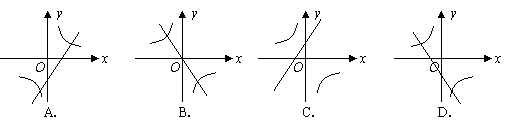
12．将函数
与函数
的大致图象画在同一坐标系中，正确的函数图象是（ ）
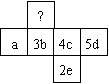13．如图是一个正方体纸盒的平面展开图，每一个正方形内部都有一个单项式．当折成正方体后，“？”所表示的单项式与对面正方形上的单项式是同类项，则“？”所表示的单项式是（ ）
A．b B．c C．d D．e
14．下列汽车标志中既是轴对称又是中心对称图形的是（ ）
大众 本田 欧宝 奥迪
A． B． C． D．
15．方程
的根的情况是（ ）
A．有两个相等的实数根 B．有两个不相等的正根
C．无实数根 D．负根的绝对值大于正根的绝对值
16．下列A、B、C、D四幅图案中，能通过平移图案（1）得到的是（ ）
 |
（1） A． B． C． D．
三、运算题（本大题共4个小题，每小题7分，满分28分）
17．计算：
．
18．先化简
，然后选择一个合适的你最喜欢的的值，代入求值．
19．已知桑塔纳小汽车的耗油量是每100km耗油15升．所使用的90#汽油今日涨价到5元/升．
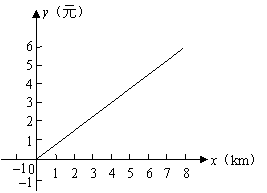
（1）写出汽车行驶途中所耗油费
（元）与行程（km）之间的函数关系式；
（2）在平面直角坐标系内描出大致的函数关系图；
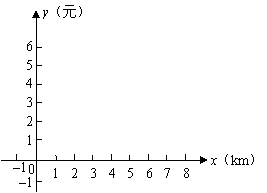（3）计算娄底到长沙220公里所需油费多少？
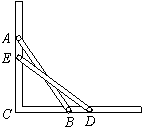
20．如图，滑杆在机械槽内运动，
为直角，已知滑杆长2.5米，顶端在
上运动，量得滑杆下端
距
点的距离为1.5米，当端点向右移动0.5米时，求滑杆顶端下滑多少米？
 |
四、操作与证明（本大题共2个小题，每小题8分，满分16分）
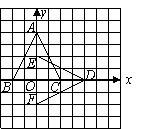
21．如图，在平面直角坐标系中，已知
的顶点坐标
，
，
．
（1）写出
的顶点坐标；
（2）将变换至要通过什么变换？请说明；
（3）画出关于轴的轴反射图形．
 |
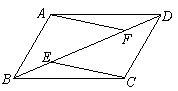
22．如图，在平行四边形中，点
是对角线
上两点，且
．
（1）写出图中每一对你认为全等的三角形；
（2）选择（1）中的任意一对全等三角形进行证明．
 |
五、实践与应用（本大题共2个小题，每小题8分，满分16分）
23．小英和小强相约一起去某超市购买他们看中的随身听和书包．你能根据他们的对话内容（如图），求出他们看中的随身听和书包单价各是多少元吗？
 |
24．娄底市为引导学生树立正确的消费观，随机调查了市内某校100名学生寒假中花零花钱的数量（钱数取整数元）．以便引导学生树立正确的消费观．根据调查数据制成了频率分布表和频率分布直方图．
频率分布表
| 分组 | 频数 | 频率 |
| 0.5~50.5 | ______ | 0.1 |
| 50.5~______ | 20 | 0.2 |
| 100.5~150.5 | ______ | ______ |
| ______~200.5 | 30 | 0.3 |
| 200.5~250.5 | 10 | 0.1 |
| 250.5~300.5 | 5 | 0.05 |
| 合计 | 100 | ______ |
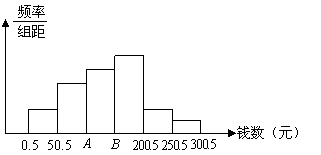
（1）补全频率分布表．
（2）大家认为，应对消费150元以上的学生提倡勤俭节约的建议．试估计应对该校1000名学生中的多少名学生提出这项建议？
六、综合探究（本大题满分12分）
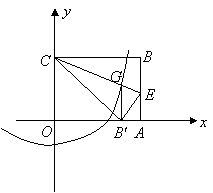
25．如图：在直角坐标系中放入一边长
为6的矩形纸片
，将纸翻折后，使点恰好落在轴上，记为
，折痕为
，已知
．
（1）求出点的坐标；
（2）求折痕所在直线的解析式；
（3）作
交于
，已知抛物线
通过点，以
为圆心
的长为半径的圆与抛物线是否还有除点以外的交点？若有，请找出这个交点坐标．
 |
数学初中毕业学业考试试卷
参考答案与评分标准
一、填空题（每小题3分，满分24分）
1．
2．
3．30 4．
5．
6．10
7．画了图案就给分 8．
二、选择题（每小题3分，选对得3分，多选、不选均得0分，满分24分）
9．C 10．D 11．B 12．D 13．D 14．D 15．D 16．B
三、运算题（每小题7分，满分21分）
17．解：原式
．
18．解：原式
．
依题意，只要
就行，如
，原式
．
19．解：（1）
即
．·········· 3分
（2）画出图象．·················································· 2分
（3）当
时，
．··········· 7分
因此，娄底到长沙220公里所需油费是165元．
20．解：设
的长为米，依题意得
．
，
．································································· 3分
，
在
中，
．························································································································· 6分
．即
．
答：梯子下滑0.5米．··································································································· 7分
21．（本题8分）解：（1）
，
，
．············································ 3分
（2）是由绕着点顺时针旋转
得到的．······································· 6分
（3）略．····················································································································· 8分
22．（本题8分）解：（1）
；
；
（每写出一对计1分）
（2）分组．
23．（本题8分）解：设他们看中的书包的单价为元，随身听的单价为元．············· 1分
依题意有
·································································································· 4分
解得
·············································································································· 7分
答：（略）····················································································································· 8分
24．（本题8分）解：（1）分组：100.5，150.5；频数：10，25；频率：0.25，1.00，每小空记1分
（2）
（人）．································································ 8分
25．（1）在
中，
，·················································· 2分
，点
．············································································· 4分
（2）由已知得：
，
，
．······································································· 5分
设
，则
，
．
，得
．
，
．············································ 6分
设直线的解析式
，
根据题意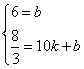得
解得：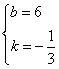
····································································· 7分
所在直线的解析式：
．······································································· 8分
（3）设
，
点在直线上，
．
．············································································································· 10分
以点为圆心，以为半径的圆的对称轴是轴，
抛物线
的对称轴也是轴．
除交点外，另有交点
，是点关于轴的对称点．
其坐标为
．······························································································· 12分