九年级（新人教版）数学专题训练（第二十七章：相似和位似）
一、选择题
1．下列命题正确的是（ ）
A．两个全等三角形一定相似
B．两个直角三角形一定相似
C．如果△ABC∽△A＇B＇C＇，那么∠A＝∠C＇，∠B＝∠A＇，∠C＝∠B＇
D．等腰三角形一定相似
2．△ABC∽△A＇B＇C＇，如果BC＝3，B＇C＇＝1.8，那么△A＇B＇C＇与△ABC的相似比为（ ）
A．5∶3 B．3∶2 C．2∶3 D．3∶5
3．已知梯形ABCD中，AD∥BC，且AC、BD相交于O，过O作EF∥AD，分别相交AB、CD于E、F，则图中共有相似三角形的对数为（ ）
A．5对 B．4对 C．3对 D．2对
4．△ABC中，D是AB上的一点，在AC上取一点E，使得以A、D、E为顶点的三角形与△ABC 相似，则这样的E点最多有（ ）
A．0个 B．1个 C．2个 D．无数个
5．下列条件中可以判定△ABC∽△A’B’C’的是（ ）
A．
B．
，∠B＝∠B＇
C．
D．，∠A＝∠A＇
6．△ABC和△DEF满足下列条件，其中使△ABC与△DEF不相似的是（ ）
A．∠A＝∠D＝45°32′，∠C=26°28′，∠E＝108°
B．BC＝a，AC＝b，AB＝c，DE＝
，EF＝
，DF＝
C． AB＝1，AC＝1.5，BC＝2，DE＝12，EF＝24，DF＝18
D．AB＝AC，DE＝DF，∠A＝∠D＝50°
7．如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB于点D，CD＝2，BD＝1，则AD的长是 （ ）
A．1
B．
C．2 D．4
8．在平行四边形ABCD中，AB＝10，AD＝6，E是AD的中点，在AB上取一点F，使△CBF∽△CDE，则AF的长是（ ）
A．5 B．8.2 C．1.8 D．6.4
9．在△ABC中，AD⊥BC于D，下列条件：①∠B+∠DAC＝90°；②∠B＝∠DAC；③
；④AB2＝BD·BC，其中一定能够判定△ABC是直角三角形的有（
）
A．0个 B．2个 C．1个 D．3个
10．如图，等腰直角△ABC中，AD是直角边BC上的中线，CE⊥AD
交AB于E，EF⊥BC于F，若AB＝BC＝4，则EF等于（ ）
A．
B．2
C．
D．
二、填空题
11．如图，已知：△ABC∽△ADE，其中∠ADE＝∠B，写出对应边的比例式： ．
12．如图，D、E、F分别是△ABC的边AB、BC、CA的中点，连结DE、EF、FD，则图中有 个三角形与△DEF相似，它们分别是 ．
13．若D、E分别是△ABC中AB、AC边上的点，当添加一个条件： 时，△ADE∽△ABC（注：只填上你认为正确的一种情况即可）．
14．已知：Rt△ABC中，∠ACB＝90°， CD⊥AB于D，若BC＝5，AC＝12，则AD＝ ，BD＝ ．
15．两个相似多边形面积的比为9：25，小多边形的周长为9cm，则大多边形的周长是 cm.
16．如图3，小李在打网球时，使球恰好能打过网，而且落在离网6米的位置（BO长），若小李击球的高度2米（CD），网高0.8米，则击球处离网距离 米.
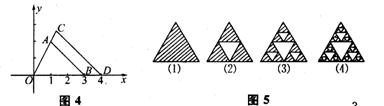
17．如图4，△AOB以O位似中心，扩大到△COD，各点坐标分别为：A（1，2）、B（3，0）、D（4，0）则点C坐标为 .
18．观察图5，若第一个图中阴影部分面积为1，第二个图中阴影部分面积为4/3，第三个图中阴影部分面积为16/9，第四图中阴影部分的面积为64/27，则第n个图中阴影部分面积为 .
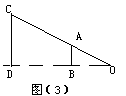
三、解答题
19、在右边的网格中描出放大的图形，
并根据图形填空。（1）相似比是多少?
（2）在适当的位置上画上坐标轴，
|
|
、
20、如图3，请你添加一个条件，使△ABCH和△ACD相似。
并说明相似过程。
21、阳光通过窗口照射到室内,在地面上留下2.7m宽的亮区(如图所示),已知亮区到窗口下的墙脚距离EC﹦8.7m,窗口高AB﹦1.8m,求窗口底边离地面的高BC.（10分）
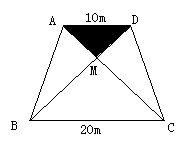22、某社区拟筹资金2000元，计划在一块上、下底分别是10米、20米的梯形空地上种植花木（如图所示），他们想在
地带种植单价为10元/米2的太阳花，当
地带种满花后，已经花了500元，请你预算一下，若继续在
地带种植同样的太阳花，资金是否够用？并说明理由。
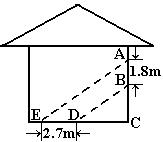
23、马戏团让狮子和公鸡表演跷跷板节目．跷跷板支柱AB的高度为1.2米．
（1）若吊环高度为2米，支点A为跷跷板PQ的中点，狮子能否将公鸡送到吊环上？为什么？
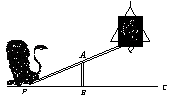（2）若吊环高度为3.6米，在不改变其他条件的前提下移动支柱，当支点A移到跷跷板PQ的什么位置时，狮子刚好能将公鸡送到吊环上？
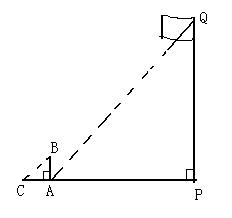
24、如图，PA为旗杆PQ的影子，小明站在A处，AC为小明的影子，在同一时刻，测得PA＝20米，AC＝2米，若小明身高AB＝1.6米.问旗杆有多高？
25、如图3，在△ABC中，AB=AC，点D、E、F分别在AB、BC、AC边上，DE﹦DF，∠EDF﹦∠A．
（1）找出图中相似的三角形，并证明；
（2）求证：
．
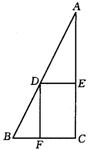
26、巳知：如图，在Rt△ABC中，∠C＝90°，BC＝4，AC＝8．点D在斜边AB上，分别作DE⊥AC，DF⊥BC，垂足分别为E、F，得四边形DECF．
设DE＝x，DF＝y．
⑴求y与x之间的函数关系式，并求出x的取值范围；
⑵设四边形DECF的面积为s，求S与x之间的函数关系式，并求出s的最大值．
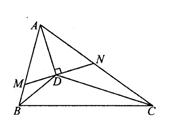27、 如图，△ABC中，三条内角平分线交于D，过D作AD垂线，分别交AB、AC于M、N，请写出图中相似的三角形，并说明其中两对相似的正确性.
28、操作题：在正方形ABCD中，P是CD上一动点（与C、D不重合），使三角尺的直角顶点与点P重合，并且一条直角边始终经过点B，另一直角边与正方形的某一边所在直线交于点E．
探究：（1）观察操作结果，哪一个三角形与△BPC相似？并证明你的结论；
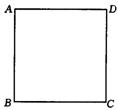（2）当点P位于CD的中点时，你找到的三角形与△BPC的周长比是多少？
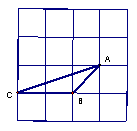
29、如图，在大小为4×4的正方形方格中，△ABC的顶点A、B、C在单位正方形的顶点上，请在图中画一个△DEF，使△DEF∽△ABC（相似比不为1），且点D、E、F都在单位正方形的顶点上。
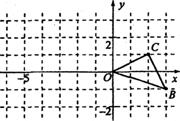
30. 如图,已知O是坐标原点，B、C两点的坐标分别为(3，-1)、(2,1)．
(1)以0点为位似中心在y轴的左侧将△OBC放大到两倍(即新图与原图的相似比为2)，画出图形；
(2)分别写出B、C两点的对应点B′、C′的坐标；
(3)如果△OBC内部一点M的坐标为(x，y),写出M的对应点M′的坐标．
31、试作四边形，使它和已知的四边形位似比等于1：２，位似中心为O使两个图形在点O同侧（保留痕迹，不写作法）.
32、 已知，连结三角形三边中点，把任意三角形分成四个小三角形，它们的形状，大小完全相同，并且与原三角形相似，如图（1）请把图（2）、（3）、（4）同样分成四块，使它们形状大小相同，且都和原图形相似，（注：图（2）为正方形，图（3）为菱形，图（4）为等腰三角形，且AD//BC，AB=CD=AD，∠B=60°）
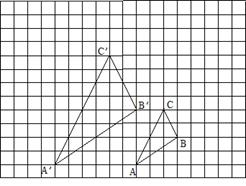
33、如图，图中的小方格都是边长为1的正方形， △ABC与△A′ B′ C′是关于点0为位似中心的位似图形，它们的顶点都在小正方形的顶点上．
(1)画出位似中心点0；
(2)求出△ABC与△A′B′C′的位似比；
(3)以点0为位似中心，再画一个△A1B1C1，使它与△ABC的位似比等于1．5．
34、在直角坐标系中,描出点A（1，3），B（2，1），C（3，1），D（0，4），
E（2，0），F（4，0），先用线段顺次连接点A、B、C，再顺次连接点D、E、F.
问：△ABC和△DEF相似吗？请说明理由.
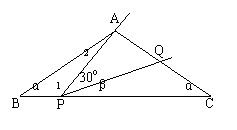
35、如图△ABC中，∠B＝∠C＝α（0<α<600）.将一把三角尺中300角顶点P放在BC边上，当P在BC边上移动时，三角尺中300角的一条边始终过点A，另一条边交AC边于点Q，P、Q不与三角形顶点重合.设∠CPQ＝β.
（1）用α、β表示∠1和∠2；
（2）①当β在许可范围内变化时，α取何值总有△ABP∽△PCQ？
②当α在许可范围内变化时，β取何值总有△ABP∽△QCP？
（3）试探索有无可能使△ABP、△QPC、△ABC两两相似？若可能，写出所有α、β的值（不写过程）；若不可能，请说明理由.
